WACE Maths Methods ATAR Paper 1 Topic Tests
Discrete Random Variables Topic Test 1
Section One: Technology-free
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
(a) The uniformly distributed continuous random variable \(X\) has an expected value of 6 and a maximum value of 9. Determine the variance of \(X\). (3 marks)
(b) The binomially distributed discrete random variable \(W\) has a mean of \(\frac{1}{2}\) and a variance of \(\frac{5}{12}\). Evaluate \(P(W = 1)\). (3 marks)
The heights reached by a species of small plant at maturity are measured by a team of biologists. The results are shown in the histogram of relative frequencies below.
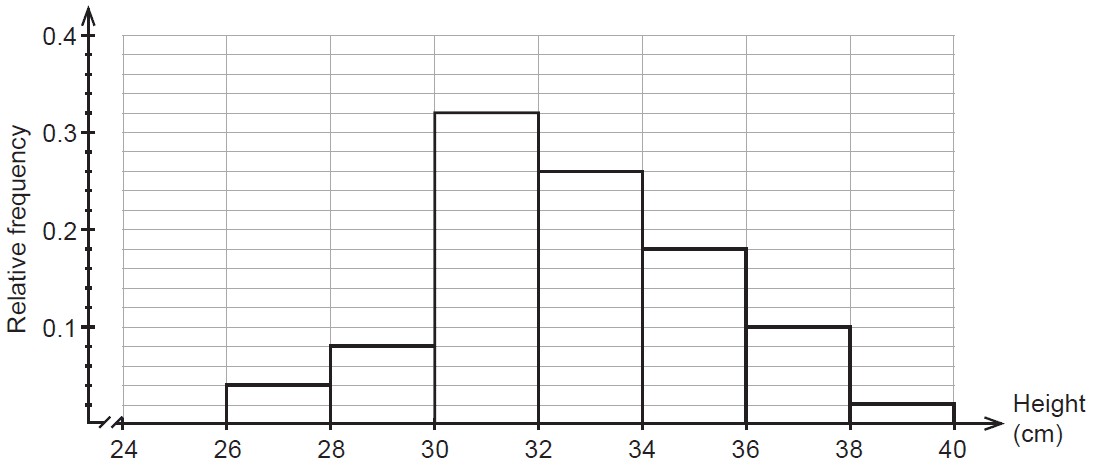
(a) Determine the probability that a mature plant of this species reaches no higher than 30 cm. (1 mark)
(b) If a mature plant reaches a height of at least 32 cm, what is the probability that its height reaches above 38 cm? (2 marks)
Another team of biologists is studying the mature heights of a species of hedge. The height, \(h\) metres, has a probability density function, \(d(h)\), as given below.
\[ d(h) = \begin{cases} \frac{h-1}{5} & \text{for } 1 \le h \le 2 \\ kh^2 & \text{for } 2 < h \le 4 \\ 0 & \text{otherwise} \end{cases} \](c) What percentage of hedges from this study reaches a mature height less than 2 m? (3 marks)
(d) Determine the value of \(k\). (3 marks)
End of questions
Discrete Random Variables Topic Test 2
Section One: Technology-free
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Ten shop owners in a coastal resort were asked how many extra staff they intended to hire for the next holiday season. Their responses are shown below:
3, 0, 2, 1, 2, 1, 1, 0, 2, 1
If \(N\) = number of additional staff,
(a) complete the probability distribution of \(N\) below. (2 marks)
| \(n\) | 0 | 1 | 2 | 3 |
| \(P(N=n)\) |
(b) what is the mean number of staff the shop owners intend to hire? (2 marks)
The tables below display the partially completed probability distribution and cumulative distribution for a discrete random variable \(X\).
| \(\boldsymbol{x}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(\boldsymbol{P(X=x)}\) | \(0.2\) | \(0.15\) | \(0.05\) |
| \(\boldsymbol{x}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(\boldsymbol{P(X \le x)}\) | \(0.2\) | \(0.6\) | \(0.95\) |
(a) Complete the missing probability entries in each of the tables above. (2 marks)
(b) Evaluate \(P(2 \le X \le 4)\). (2 marks)
(c) Evaluate \(P(X = 1 | X \le 3)\). (2 marks)
Anastasia is a university student. She records the time it takes for her to get from home to her campus each day. The histogram of relative frequencies below shows the journey times she recorded.
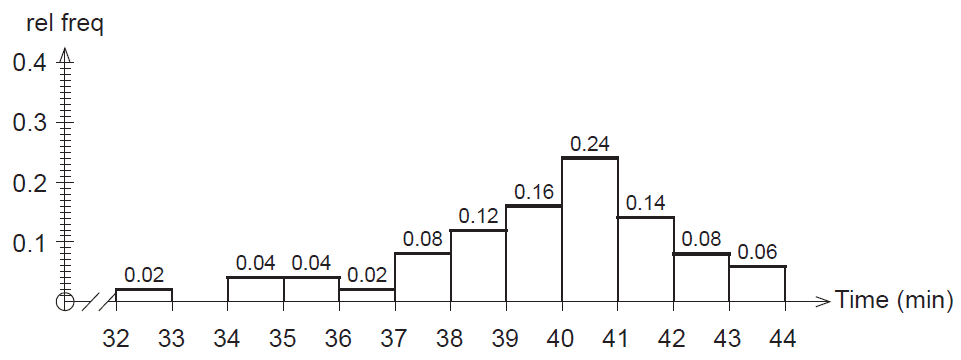
Use the above data to estimate the probability of her next journey from home to her university campus
(a) taking her less than 36 minutes. (1 mark)
(b) taking at least 35 minutes but no more than 39 minutes. (2 marks)
On three consecutive days, Anastasia needs to be on campus no later than 10 am.
(c) If she leaves her home at 9:22 am each day, use the above data to estimate the probability that she makes it on or before time on all three days. (2 marks)
End of questions
Discrete Random Variables Topic Test 3
Section One: Technology-free
Number of marks: 10
Reading time: 1 minute
Writing time: 10 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
It takes Nahyun between 15 and 40 minutes to get to school each day, depending on traffic conditions. Nahyun leaves home for school at 8:00 am each school day. Let the random variable \(X\) be the time, in minutes after 8:00 am, that Nahyun arrives at school. The probability density function of \(X\) is shown below.
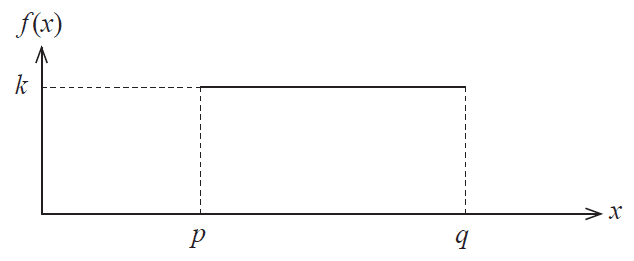
(a) What is the name of this type of distribution? (1 mark)
(b) Determine:
(i) the values of \(p\), \(q\) and \(k\) (2 marks)
(ii) the expected value of \(X\) (1 mark)
(iii) the probability that Nahyun arrives at school before 8:25 am. (2 marks)
Nahyun will be late for her first class if she arrives at school after 8:28 am. Otherwise, she will not be late.
(c) If Nahyun is not late for her first class, what is the probability that she arrives after 8:25 am? (2 marks)
(d) If Nahyun only wants to be late for her first class at most 4% of the time, what time should she leave home, assuming the 15 to 40 minute travel time remains the same? (2 marks)
End of questions
Discrete Random Variables Topic Test 4
Section One: Technology-free
Number of marks: 9
Reading time: 1 minute
Writing time: 9 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The heights reached by a species of small plant at maturity are measured by a team of biologists. The results are shown in the histogram of relative frequencies below.

(a) Determine the probability that a mature plant of this species reaches no higher than 30 cm. (1 mark)
(b) If a mature plant reaches a height of at least 32 cm, what is the probability that its height reaches above 38 cm? (2 marks)
Another team of biologists is studying the mature heights of a species of hedge. The height, \(h\) metres, has a probability density function, \(d(h)\), as given below.
\[ d(h) = \begin{cases} \frac{h-1}{5} & \text{for } 1 \le h \le 2 \\ kh^2 & \text{for } 2 < h \le 4 \\ 0 & \text{otherwise} \end{cases} \]
(c) What percentage of hedges from this study reaches a mature height less than 2 m? (3 marks)
(d) Determine the value of \(k\). (3 marks)
End of questions
Discrete Random Variables Topic Test 5
Section One: Technology-free
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Michelle is a soccer goalkeeper and has built a machine to help her practise. The machine will shoot a soccer ball randomly along the ground at or near a goal that is seven metres wide. The machine is equally likely to shoot the ball so that the centre of the ball crosses the goal line anywhere between point A three metres left of the goal, and point B five metres right of the goal, as shown in the diagram below.
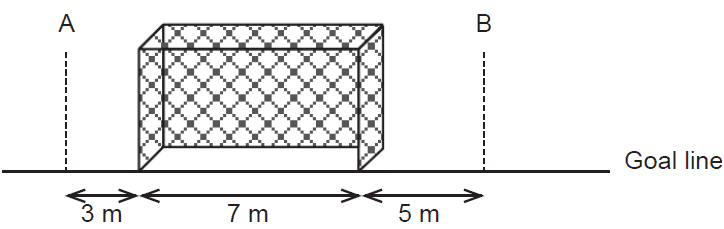
Michelle sets up a trial run without anyone in the goals. Assume the goal posts are of negligible width.
Let the random variable \(X\) be the distance the centre of the ball crosses the goal line to the right of point A.
(a) Complete the graphical representation of the probability density function for the random variable \(X\). (2 marks)

(b) What is the probability that the machine shoots a ball so that its centre misses the goal to the left? (1 mark)
(c) What is the probability that the machine shoots a ball so that its centre is inside the goal? (1 mark)
(d) If the machine shoots a ball so that its centre misses the goal, what is the probability that the ball's centre misses to the right? (2 marks)
Waiting times for patients at a hospital emergency department can be up to four hours. The associated probability density function is shown below.
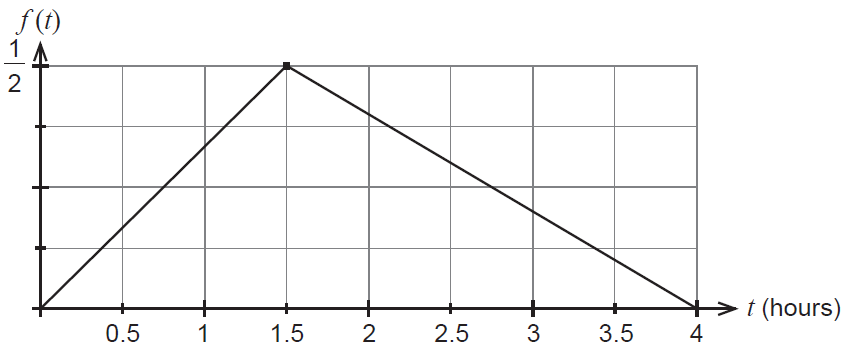
(a) What is the probability a patient will wait less than one hour? (3 marks)
(b) What is the probability a patient will wait between one hour and three hours? (4 marks)
End of questions
Discrete Random Variables Topic Test 6
Section One: Technology-free
Number of marks: 10
Reading time: 1 minute
Writing time: 10 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Solcolwa is a green energy company that owns 20 solar farms across Western Australia. The generation capacities, in megawatts (MW), of the solar farms are displayed in the histogram below.
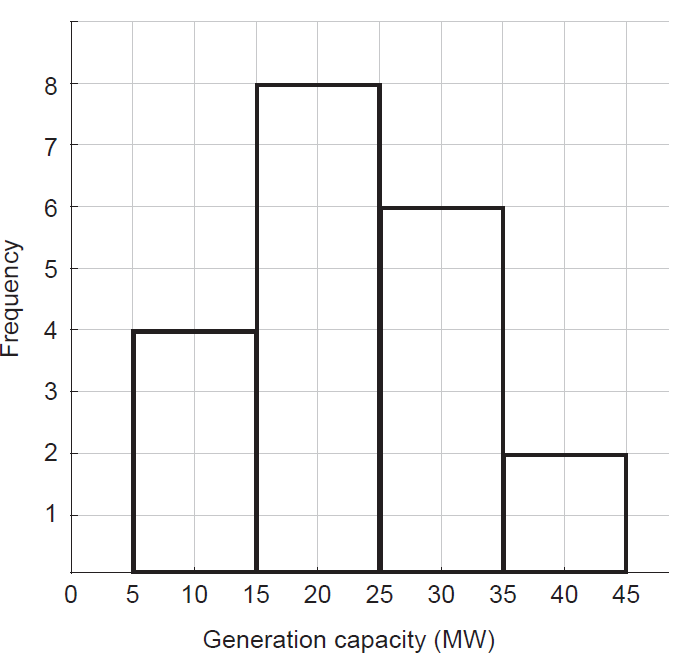
Suppose that one of the Solcolwa solar farms is selected at random. Let the random variable \(W\) denote the generation capacity of the randomly-selected solar farm.
(a) Complete the following table of cumulative probabilities for \(W\). (2 marks)
| \(w\) | 5 | 15 | 25 | 35 | 45 |
|---|---|---|---|---|---|
| \(P(W \le w)\) | 0 | 0.2 | 0.6 | 0.9 | 1 |
(b) Determine \(P(W \ge 35)\). (1 mark)
(c)
(i) estimate \(P(W \ge 20)\). (2 marks)
(ii) estimate the expected value \(E(W)\). (2 marks)
(d) Given that \(Y = aW\) and that \(W\) and \(Y\) have variances \(\text{Var}(W) = 81\) and \(\text{Var}(Y) = 324\), determine the expected value \(E(Y)\). (3 marks)
End of questions


