VCE Maths Methods Trigonometry Mini Test 3
Number of marks: 10
Reading time: 2 minutes
Writing time: 15 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The amplitude, \( A \), and the period, \( P \), of the function \( f(x) = -\frac{1}{2} \sin(3x + 2\pi) \) are
- A. \( A = -\frac{1}{2}, \quad P = \frac{\pi}{3} \)
- B. \( A = -\frac{1}{2}, \quad P = \frac{2\pi}{3} \)
- C. \( A = -\frac{1}{2}, \quad P = \frac{3\pi}{2} \)
- D. \( A = \frac{1}{2}, \quad P = \frac{\pi}{3} \)
- E. \( A = \frac{1}{2}, \quad P = \frac{2\pi}{3} \)
The solutions of the equation \(2\cos\left(2x - \frac{\pi}{3}\right) + 1 = 0\) are
- A. \(x = \frac{\pi(6k-2)}{6}\) or \(x = \frac{\pi(6k-3)}{6}\), for \(k \in Z\)
- B. \(x = \frac{\pi(6k-2)}{6}\) or \(x = \frac{\pi(6k+5)}{6}\), for \(k \in Z\)
- C. \(x = \frac{\pi(6k-1)}{6}\) or \(x = \frac{\pi(6k+2)}{6}\), for \(k \in Z\)
- D. \(x = \frac{\pi(6k-1)}{6}\) or \(x = \frac{\pi(6k+3)}{6}\), for \(k \in Z\)
- E. \(x = \pi\) or \(x = \frac{\pi(6k+2)}{6}\), for \(k \in Z\)
The sum of the solutions of \(\sin(2x) = \frac{\sqrt{3}}{2}\) over the interval \([-\pi, d]\) is \(-\pi\).
The value of \(d\) could be
- A. 0
- B. \(\frac{\pi}{6}\)
- C. \(\frac{3\pi}{4}\)
- D. \(\frac{7\pi}{6}\)
- E. \(\frac{3\pi}{2}\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Solve \(1 - \cos(\frac{x}{2}) = \cos(\frac{x}{2})\) for \(x \in [-2\pi, \pi]\). 2 marks
b. The function \(f: [-2\pi, \pi] \to \mathbb{R}\), \(f(x) = \cos(\frac{x}{2})\) is shown on the axes below.
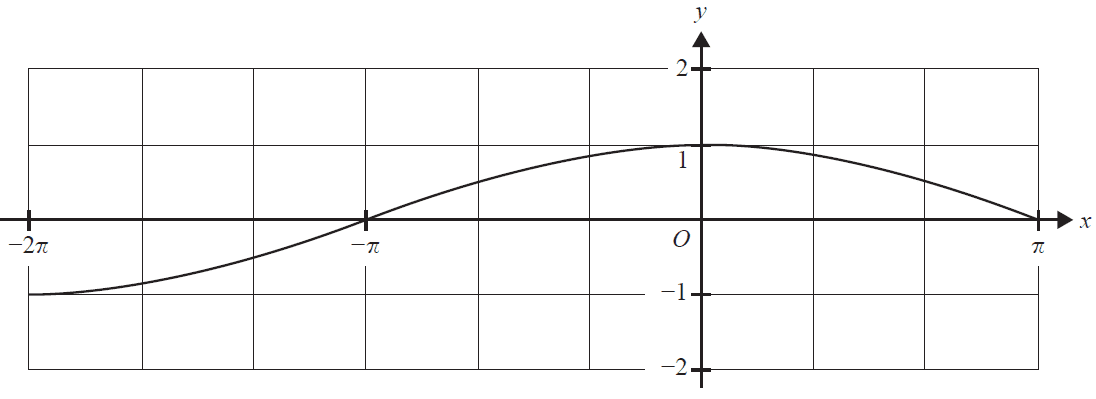
Let \(g: [-2\pi, \pi] \to \mathbb{R}\), \(g(x) = 1 - f(x)\).
Sketch the graph of \(g\) on the axes above. Label all points of intersection of the graphs of \(f\) and \(g\), and the endpoints of \(g\), with their coordinates. 2 marks
Let \((\tan(\theta)-1)(\sin(\theta)-\sqrt{3}\cos(\theta))(\sin(\theta)+\sqrt{3}\cos(\theta)) = 0\).
a. State all possible values of \(\tan(\theta)\). 1 mark
b. Hence, find all possible solutions for \((\tan(\theta)-1)(\sin^2(\theta)-3\cos^2(\theta)) = 0\), where \(0 \le \theta \le \pi\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au