2024 VCAA Maths Methods Exam 2
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 80
Reading time: 15 minutes
Writing time: 2 hours
Section A ā Multiple-choice questions
Instructions
ā¢ Answer all questions in pencil on your Multiple-Choice Answer Sheet.
ā¢ Choose the response that is correct for the question.
ā¢ A correct answer scores 1; an incorrect answer scores 0.
ā¢ Marks will not be deducted for incorrect answers.
ā¢ No marks will be given if more than one answer is completed for any question.
ā¢ Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Let \( y = e^x \cos(3x) \).
Find \( \frac{dy}{dx} \). 1 mark
b. Let \( f(x) = \log_e(x^3 - 3x + 2) \). Find \( f'(3) \). 2 marks
Consider the simultaneous linear equations
\( 3k x - 2y = k + 4 \)
\( (k - 4)x + ky = -k \)
where \( x, y \in \mathbb{R} \) and \( k \) is a real constant.
Determine the value of \( k \) for which the system of equations has no real solution. 3 marks
Let \( g : \mathbb{R} \setminus \{-3\} \rightarrow \mathbb{R},\ g(x) = \frac{1}{x + 3} - 2 \).
a. On the axes below, sketch the graph of \( y = g(x) \), labelling all asymptotes with their equations and axis intercepts with their coordinates. 2 marks
b. Determine the area of the region bounded by the line \( x = -2 \), the x-axis, the y-axis and the graph of \( y = g(x) \). 3 marks
Let \( X \) be a binomial random variable where \( X \sim \text{Bi}\left(4, \frac{9}{10}\right) \).
a. Find the standard deviation of \( X \). 1 mark
b. Find \( \Pr(X < 2) \). 2 marks
The function \( h : [0, \infty) \rightarrow \mathbb{R},\ h(t) = \frac{3000}{t + 1} \) models the population of a town after \( t \) years.
a. Use the model \( h(t) \) to predict the population of the town after four years. 1 mark
b. A new function, \( h_1 \), models a population where \( h_1(0) = h(0) \) but \( h_1 \) decreases at half the rate of \( h \) at any point in time.
State a sequence of two transformations that maps \( h \) to this new model \( h_1 \). 2 marks
c. In the town, 100 people were randomly selected and surveyed, with 60 people indicating that they were unhappy with the roads.
i. Determine an approximate 95% confidence interval for the proportion of people in the town who are unhappy with the roads. Use \( z = 2 \) for this confidence interval. 2 marks
ii. A new sample of \( n \) people results in the same sample proportion.
Find the smallest value of \( n \) to achieve a standard deviation of \( \frac{\sqrt{2}}{50} \) for the sample proportion. 1 mark
Solve \( 2\log_3(x - 4) + \log_3(x) = 2 \) for \( x \). 4 marks
Part of the graph of \( f : [-\pi, \pi] \rightarrow \mathbb{R},\ f(x) = x\sin(x) \) is shown below.
a. Use the trapezium rule with a step size of \( \frac{\pi}{3} \) to determine an approximation of the total area between the graph of \( y = f(x) \) and the x-axis over the interval \( x \in [0, \pi] \). 3 marks
b.
i. Find \( f'(x) \). 1 mark
ii. Determine the range of \( f'(x) \) over the interval \( \left[\frac{\pi}{3}, \frac{2\pi}{3} \right] \). 1 mark
iii. Hence, verify that \( f(x) \) has a stationary point for \( x \in \left[\frac{\pi}{3}, \frac{2\pi}{3} \right] \). 1 mark
c. On the set of axes below, sketch the graph of \( y = f'(x) \) on the domain \( [-\pi, \pi] \), labelling the endpoints with their coordinates.
You may use the fact that the graph of \( y = f'(x) \) has a local minimum at approximately \( (-1.1, -1.4) \) and a local maximum at approximately \( (1.1, 1.4) \). 3 marks
Let \( g : \mathbb{R} \rightarrow \mathbb{R}, \quad g(x) = \sqrt[3]{x - k}+ m, \quad \text{where } k \in \mathbb{R} \setminus \{0\} \text{ and } m \in \mathbb{R} \).
Let the point \( P \) be the y-intercept of the graph of \( y = g(x) \).
a. Find the coordinates of \( P \), in terms of \( k \) and \( m \). 1 mark
b. Find the gradient of \( g \) at \( P \), in terms of \( k \). 2 marks
c. Given that the graph of \( y = g(x) \) passes through the origin, express \( k \) in terms of \( m \). 1 mark
d. Let the point \( Q \) be a point different from the point \( P \), such that the gradient of \( g \) at points \( P \) and \( Q \) are equal.
Given that the graph of \( y = g(x) \) passes through the origin, find the coordinates of \( Q \) in terms of \( m \). 3 marks
The asymptote(s) of the graph of \( y = \log_e(x + 1) - 3 \) are
- A. \( x = -1\) only
- B. \( x = 1\) only
- C. \( y = -3\) only
- D. \( x = -1\) and \( y = -3 \)
A function \( g: \mathbb{R} \to \mathbb{R} \) has the derivative \( g'(x) = x^3 - x \).
Given that \( g(0) = 5 \), the value of \( g(2) \) is
- A. 2
- B. 3
- C. 5
- D. 7
A discrete random variable \( X \) is defined using the probability distribution below, where \( k \) is a positive real number.
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Pr(X = x) | 2k | 3k | 5k | 3k | 2k |
Find \( \Pr(X < 4 \mid X > 1) \).
- A. \(\frac{13}{15}\)
- B. \(\frac{11}{13}\)
- C. \(\frac{4}{5}\)
- D. \(\frac{8}{15}\)
If \( \int_a^b f(x)\,dx = -5 \) and \( \int_a^c f(x)\,dx = 3 \), where \( a < b < c \), then \( \int_b^c 2f(x)\,dx \) is equal to
- A. -16
- B. 16
- C. -4
- D. 4
Consider the functions \( f : (1, \infty) \to \mathbb{R}, f(x) = x^2 - 4x \) and \( g: \mathbb{R} \to \mathbb{R}, g(x) = e^{-x} \)
The range of the composite function \( g(f(x)) \) is
- A. \( (0, e^3) \)
- B. \( (0, e^3] \)
- C. \( (0, e^4) \)
- D. \( (0, e^4] \)
Consider the function \( f(x) = \frac{2x+1}{3-x} \), with domain \( x \in \mathbb{R} \setminus \{3\} \).
The inverse of \( f \) is
- A. \( f^{-1}(x) = \frac{3x - 1}{x + 2} \) with domain \( x \in \mathbb{R} \setminus \{3\} \)
- B. \( f^{-1}(x) = 3 - \frac{7}{x + 2} \) with domain \( x \in \mathbb{R} \setminus \{-2\} \)
- C. \( f^{-1}(x) = 3 + \frac{5}{x + 2} \) with domain \( x \in \mathbb{R} \setminus \{-2\} \)
- D. \( f^{-1}(x) = \frac{1 - 3x}{x + 2} \) with domain \( x \in \mathbb{R} \setminus \{-2\} \)
A fair six-sided die is repeatedly rolled. What is the minimum number of rolls required so that the probability of rolling a six at least once is greater than 0.95?
- A. 15
- B. 16
- C. 17
- D. 18
Some values of the functions \( f: \mathbb{R} \to \mathbb{R} \) and \( g: \mathbb{R} \to \mathbb{R} \) are shown below.
| x | 1 | 2 | 3 |
|---|---|---|---|
| f(x) | 0 | 4 | 5 |
| g(x) | 3 | 4 | -5 |
The graph of the function \( h(x) = f(x) - g(x) \) must have an x-intercept at
- A. (2, 0)
- B. (3, 0)
- C. (4, 0)
- D. (5, 0)
At a Year 12 formal, 45% of the students travelled to the event in a hired limousine, while the remaining 55% were driven by a parent.
Of the students who travelled in a hired limousine, 30% had a professional photo taken.
Of the students who were driven by a parent, 60% had a professional photo taken.
Given that a student had a professional photo taken, what is the probability that the student travelled in a hired limousine?
- A. \(\frac{1}{8}\)
- B. \(\frac{27}{200}\)
- C. \(\frac{9}{31}\)
- D. \(\frac{22}{31}\)
Suppose a function \( f: [0, 5] \to \mathbb{R} \) and its derivative \( f': [0, 5] \to \mathbb{R} \) are defined and continuous on their domains.
If \( f'(2) < 0 \) and \( f'(4) > 0 \), which one of these statements must be true?
- A. f is strictly decreasing on [0, 2]
- B. f does not have an inverse function
- C. f is positive on [4, 5]
- D. f has a local minimum at x = 3
Twelve students sit in a classroom, with seven students in the first row and five in the second row. Three students are chosen randomly from the class.
The probability that exactly two of the three students chosen are in the first row is
- A. \(\frac{7}{44}\)
- B. \(\frac{21}{44}\)
- C. \(\frac{5}{22}\)
- D. \(\frac{245}{576}\)
The graph of \( y = f(x) \) is shown below
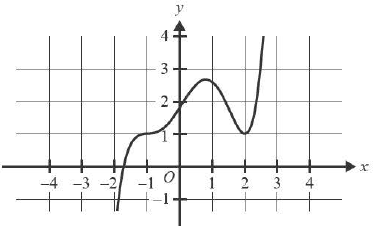
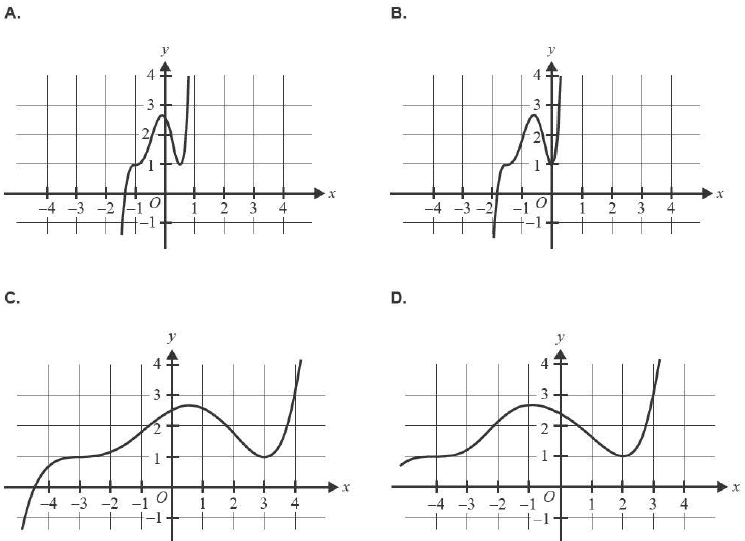
Which of the following options best represents the graph of \( y = f(2x + 1) \)?
The function \( f: (0, \infty) \to \mathbb{R}, f(x) = \frac{x}{2}+\frac{2}{x} \) is mapped to a function \( g \) by:
1. dilation by a factor of 3 from the y-axis
2. translation by 1 unit in the negative y-direction
The function \( g \) has a local minimum at
- A. (6, 1)
- B. \((\frac{2}{3}, 1)\)
- C. (2, 5)
- D. \((2, -\frac{1}{3})\)
Let \( h \) be the probability density function for a continuous random variable \( X \), where
\[ h(x) = \begin{cases} \dfrac{x}{6} + k, & \text{for } -3 \leq x < 0 \\ -\dfrac{x}{2} + k, & \text{for } 0 \leq x \leq 1 \\ 0, & \text{elsewhere} \end{cases} \]
and \( k \) is a positive real number.
The value of \( \Pr(X < 0.5) \) is
- A. \(\frac{1}{2}\)
- B. \(\frac{15}{16}\)
- C. \(\frac{3}{16}\)
- D. \(\frac{49}{48}\)
The points of inflection of the graph of \( y = 2 - \tan(\pi(x - \tfrac{1}{4})) \) are
- A. \((k + \tfrac{1}{4}, 2), k \in \mathbb{Z}\)
- B. \((k - \tfrac{1}{4}, 2), k \in \mathbb{Z}\)
- C. \((k + \tfrac{1}{4}, -2), k \in \mathbb{Z}\)
- D. \((k - \tfrac{3}{4}, -2), k \in \mathbb{Z}\)
Suppose that a differentiable function \( f: \mathbb{R} \to \mathbb{R} \) and its derivative \( f' : \mathbb{R} \to \mathbb{R} \) satisfy \( f(4) = 25 \) and \( f'(4) = 15 \).
Determine the gradient of the tangent line to the graph of \( y = \sqrt{f(x)} \) at \( x = 4 \).
- A. \(\sqrt{15}\)
- B. \(\frac{1}{10}\)
- C. \(\frac{15}{2}\)
- D. \(\frac{3}{2}\)
Consider the algorithm below which prints the roots of the cubic polynomial \( f(x) = x^3 - 2x^2 - 9x + 18 \).
The algorithm prints in order:
- A. -3, 3, 2
- B. -3, 2, 3
- C. 3, 2, -3
- D. 3, -3, 2
Find the value of \( x \) which maximises the area of the trapezium shown below.
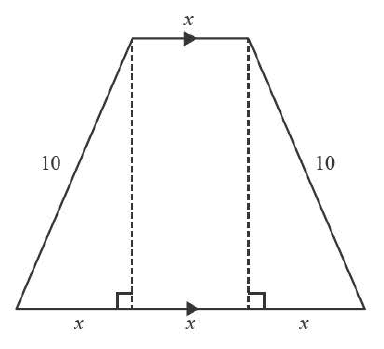
- A. 10
- B. 5\(\sqrt{2}\)
- C. 7
- D. \(\sqrt{10}\)
Consider the normal random variable \( X \) such that \( \Pr(X < 10) = 0.2 \) and \( \Pr(X > 18) = 0.2 \).
The value of \( \Pr(X < 12) \) is closest to
- A. 0.134
- B. 0.297
- C. 0.337
- D. 0.365
The function \( f: \mathbb{R} \to \mathbb{R} \) has average value \( k \) on the interval [0, 2] and satisfies \( f(x) = f(x + 2) \) for all \( x \in \mathbb{R} \).
The value of the definite integral \( \int_2^6 f(x)\,dx \) is
- A. 2k
- B. 3k
- C. 4k
- D. 6k
End of Section A
Section B
Instructions
ā¢ Answer all questions in the spaces provided.
ā¢ Write your responses in English.
ā¢ In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
ā¢ In questions where more than one mark is available, appropriate working must be shown.
ā¢ Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Consider the function \( f: \mathbb{R} \rightarrow \mathbb{R},\ f(x) = (x + 1)(x + a)(x - 2)(x - 2a) \) where \( a \in \mathbb{R} \).
a. State, in terms of \( a \) where required, the values of \( x \) for which \( f(x) = 0 \). 1 mark
b. Find the values of \( a \) for which the graph of \( y = f(x) \) has
i. exactly three x-intercepts. 2 marks
ii. exactly four x-intercepts. 1 mark
c. Let \( g \) be the function \( g: \mathbb{R} \rightarrow \mathbb{R},\ g(x) = (x + 1)^2(x - 2)^2 \), which is the function \( f \) where \( a = 1 \).
i. Find \( g'(x) \). 1 mark
ii. Find the coordinates of the local maximum of \( g \). 1 mark
iii. Find the values of \( x \) for which \( g'(x) > 0 \). 1 mark
iv. Consider the two tangent lines to the graph of \( y = g(x) \) at the points where \( x =\frac{-\sqrt{3} + 1}{2} \) and \( x = \frac{\sqrt{3} + 1}{2} \). Determine the coordinates of the point of intersection of these two tangent lines. 2 marks
d. Let \( g \) remain as the function \( g: \mathbb{R} \rightarrow \mathbb{R},\ g(x) = (x + 1)^2(x - 2)^2 \), which is the function \( f \) where \( a = 1 \).
Let \( h \) be the function \( h: \mathbb{R} \rightarrow \mathbb{R},h(x) = (x + 1)(x - 1)(x + 2)(x - 2) \), which is the function \( f \) where \( a = -1 \).
i. Using translations only, describe a sequence of transformations of \( h \), for which its image would have a local maximum at the same coordinates as that of \( g \). 1 mark
ii. Using a dilation and translations, describe a different sequence of transformations of \( h \), for which its image would have both local minimums at the same coordinates as that of \( g \). 2 marks
A model for the temperature in a room, in degrees Celsius, is given by
a. Express the derivative \( f'(t) \) as a hybrid function. 2 marks
b. Find the average rate of change in temperature predicted by the model between \( t = 0 \) and \( t = \frac{1}{2} \). Give your answer in degrees Celsius per hour. 1 mark
c. Another model for the temperature in the room is given by \( g(t) = 22 - 10e^{-6t},\ t \geq 0 \).
i. Find the derivative \( g'(t) \). 1 mark
ii. Find the value of \( t \) for which \( g'(t) = 10 \). Give your answer correct to three decimal places. 1 mark
d. Find the time \( t \in (0, 1) \) when the temperatures predicted by the models \( f \) and \( g \) are equal. Give your answer correct to two decimal places. 1 mark
e. Find the time \( t \in (0, 1) \) when the difference between the temperatures predicted by the two models is the greatest. Give your answer correct to two decimal places. 1 mark
f. The amount of power, in kilowatts, used by the heater \( t \) hours after it is switched on, can be modelled by the continuous function \( p \), whose graph is shown below.
\\[ p(t) = \begin{cases} 1.5 & 0 \leq t \leq 0.4 \\ 0.3 + Ae^{-10t} & t > 0.4 \end{cases} \]
The amount of energy used by the heater, in kilowatt hours, can be estimated by evaluating the area between the graph of \( y = p(t) \) and the \( t \)-axis.
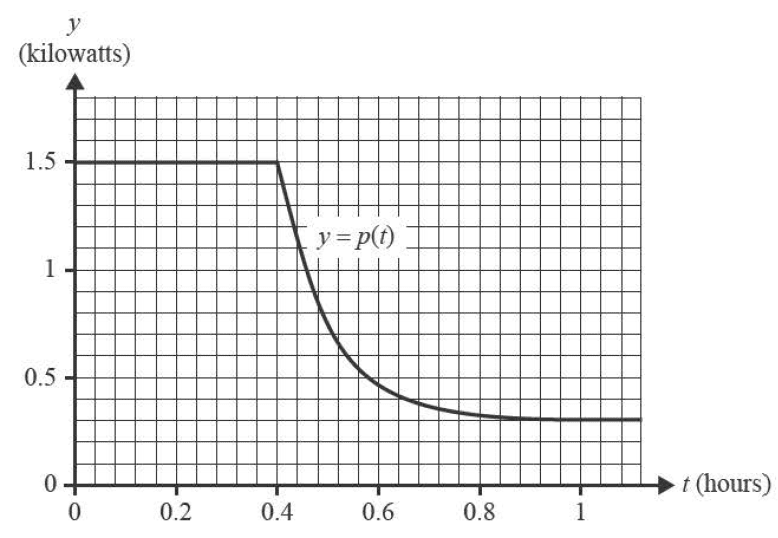
i. Given that \( p(t) \) is continuous for \( t \geq 0 \), show that \( A = 1.2e^4 \). 1 mark
ii. Find how long it takes, after the heater is switched on, until the heater has used 0.5 kilowatt hours of energy. Give your answer in hours. 1 mark
iii. Find how long it takes, after the heater is switched on, until the heater has used 1 kilowatt hour of energy. Give your answer in hours, correct to two decimal places. 2 marks
The points shown on the chart below represent monthly online sales in Australia.
The variable \( y \) represents sales in millions of dollars.
The variable \( t \) represents the month when the sales were made, where \( t = 1 \) corresponds to January 2021, \( t = 2 \) corresponds to February 2021 and so on.
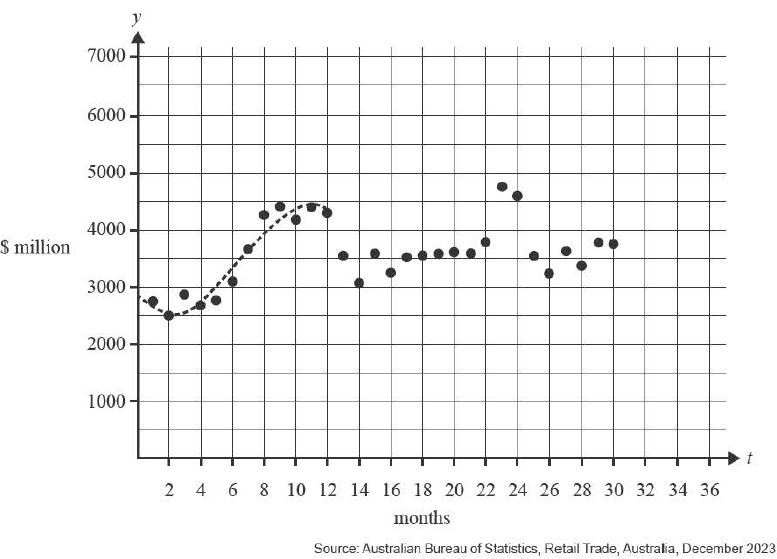
a. A cubic polynomial \( p : (0, 12] \rightarrow \mathbb{R}, \, p(t) = at^3 + bt^2 + ct + d \) can be used to model monthly online sales in 2021.
The graph of \( y = p(t) \) is shown as a dashed curve on the set of axes above.
It has a local minimum at (2, 2500) and a local maximum at (11, 4400).
i. Find, correct to two decimal places, the values of \( a \), \( b \), \( c \) and \( d \). 3 marks
ii. Let \( q : (12, 24] \rightarrow \mathbb{R}, \, q(t) = p(t - h) + k \) be a cubic function obtained by translating \( p \), which can be used to model monthly online sales in 2022.
Find the values of \( h \) and \( k \) such that the graph of \( y = q(t) \) has a local maximum at (23, 4750). 2 marks
b. Another function \( f \) can be used to model monthly online sales, where
\( f : (0, 36] \rightarrow \mathbb{R}, \quad f(t) = 3000 + 30t + 700\cos\left(\frac{\pi t}{6}\right) + 400\cos\left(\frac{\pi t}{3}\right) \)
Part of the graph of \( f \) is shown on the axes below.
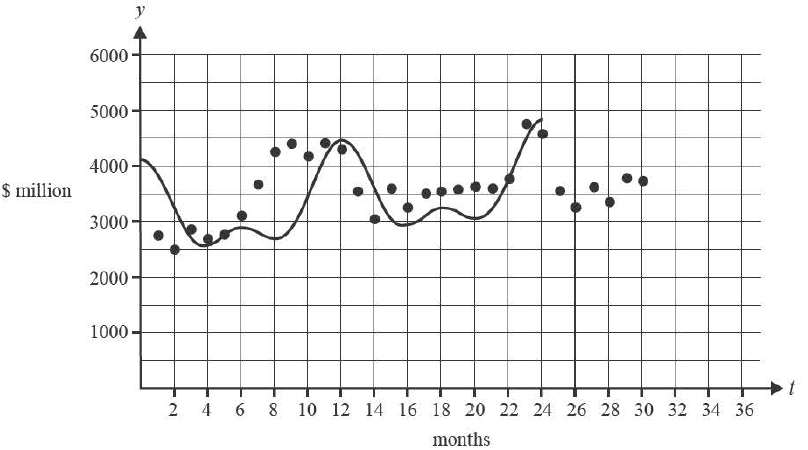
i. Complete the graph of \( f \) on the set of axes above until December 2023, that is, for \( t \in (24, 36] \).
Label the endpoint at \( t = 36 \) with its coordinates. 2 marks
ii. The function \( f \) predicts that every 12 months, monthly online sales increase by \( n \) million dollars.
Find the value of \( n \). 1 mark
iii. Find the derivative \( f'(t) \). 1 mark
iv. Hence, find the maximum instantaneous rate of change for the function \( f \), correct to the nearest million dollars per month, and the values of \( t \) in the interval \( (0, 36] \) when this maximum rate occurs, correct to one decimal place. 2 marks
At an airport, luggage is weighed before it is checked in.
The mass of each piece of luggage, in kilograms, is modelled by a continuous random variable \( X \), whose probability density function is
\[ f(x) = \begin{cases} \frac{1}{67500} x^2(30 - x), & 0 \leq x \leq 30 \\ 0, & \text{elsewhere} \end{cases} \]
A piece of luggage is labelled as heavy if its mass exceeds 23 kg.
a. Write a definite integral which gives the probability that a piece of luggage is labelled as heavy. 1 mark
b.
i. Find the mean of \( X \). 1 mark
ii. Find the standard deviation of \( X \). 2 marks
iii. Given that the mass of a piece of luggage is more than the mean, find the probability that it is labelled as heavy, correct to three decimal places. 2 marks
Use the following information to answer parts c and d of this question.
Of the travellers flying from the airport
- ā¢ 10% do not check in any luggage
- ā¢ 40% check in exactly one piece of luggage
- ā¢ 50% check in exactly two pieces of luggage
Assume that the mass of each piece of luggage is independent of the number of pieces checked in by each traveller.
Use the value of 0.234 for the probability that a piece of luggage is labelled as heavy.
c. Let \( W \) be the discrete random variable that represents the number of pieces of luggage labelled as heavy checked in by each traveller.
i. Show that \( \Pr(W = 2) = 0.027 \), correct to three decimal places. 1 mark
ii. Complete the table below for the probability distribution \( W \), correct to three decimal places. 2 marks
\[ \begin{array}{|c|c|c|c|} \hline w & 0 & 1 & 2 \\ \hline \Pr(W = w) & & & 0.027 \\ \hline \end{array} \]
d. On a particular day, a random sample of 35 pieces of luggage was selected at the airport.
Let \( \hat{P} \) be the random variable that represents the proportion of luggage labelled as heavy in random samples of 35.
i. Find \( \Pr(\hat{P} > 0.2) \), correct to three decimal places. 2 marks
ii. Determine the probability that \( \hat{P} \) lies within one standard deviation of its mean, correct to three decimal places. Do not use a normal approximation. 2 marks
e.
i. In one random sample of 50 pieces of luggage, 10 are labelled as heavy. Use this sample to find an approximate 90% confidence interval for \( p \), the population proportion of luggage labelled as heavy, correct to three decimal places. 1 mark
ii. A second random sample of 50 pieces of luggage is selected. Using this sample, the approximate 90% confidence interval for \( p \), the population proportion of luggage labelled as heavy, is wider than the one obtained above in part e.i.
State the minimum and maximum possible number of pieces of luggage labelled as heavy in the second sample. 1 mark
The graph below shows the compositions \( g \circ f \) and \( f \circ g \), where \( f(x) = \sin(x) \) and \( g(x) = \sin(2x) \).
a.
i. The graph of \( y = (g \circ f)(x) \) has a local maximum whose \( x \)-value lies in the interval \( [0, \frac{\pi}{2}] \).
Find the coordinates of this local maximum, correct to one decimal place. 1 mark
ii. State the range of \( g \circ f \) where \( x \in [0, 2\pi] \). 1 mark
b.
i. Find the derivative of \( f \circ g \). 1 mark
ii. Show that the equation \( \cos(\sin(2x)) = 0 \) has no real solutions. 2 marks
iii. Find the \( x \)-values of the stationary points of \( f \circ g \) where \( x \in [0, 2\pi] \). 1 mark
iv. Find the range of \( f \circ g \) where \( x \in [0, 2\pi] \). 1 mark
c.
i. Write a single definite integral that gives the area bounded by the graphs of \( y = (f \circ g)(x) \) and \( y = (g \circ f)(x) \) in the interval \( [0, 2\pi] \). 1 mark
ii. Hence, state the area bounded by the graphs of \( y = (f \circ g)(x) \) and \( y = (g \circ f)(x) \) in the interval \( [0, 2\pi] \), correct to two decimal places. 1 mark
d. Let \( f_1 : (0, 2\pi) \rightarrow \mathbb{R}, \, f_1(x) = \sin(x) \).
Find all values of \( x \) in the interval \( (0, 2\pi) \) for which the composition \( f_1 \circ g \) is defined. 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
