WACE Maths Methods ATAR Paper 1 Topic Tests

Question 1 (10 marks) [2024 Section 1 Q2]

An advertising graphic moves across the bottom of a television screen during a sporting game, changing direction to attract viewer attention. The position of the graphic is modelled by \[x(t) = \frac{1}{3}t^3 - 7t^2 + 40t\] where \(x\), in centimetres, is the position of the graphic relative to the left side of the screen, and \(t\), in seconds, is the time from when the graphic first appears on the screen.

The position of the graphic at integer time increments is given in the table below.

\(\boldsymbol{t}\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
\(\boldsymbol{x(t)}\)	\(0\)	\(33\frac{1}{3}\)	\(54\frac{2}{3}\)	\(66\)	\(69\frac{1}{3}\)	\(66\frac{2}{3}\)	\(60\)	\(51\frac{1}{3}\)
\(\boldsymbol{t}\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)	\(13\)	\(14\)	\(15\)
\(\boldsymbol{x(t)}\)	\(42\frac{2}{3}\)	\(36\)	\(33\frac{1}{3}\)	\(36\frac{2}{3}\)	\(48\)	\(69\frac{1}{3}\)	\(102\frac{2}{3}\)	\(150\)

(a) Determine the velocity of the graphic when it first appears on the screen. (2 marks)

(b) Is the graphic initially speeding up or slowing down? Justify your answer. (2 marks)

(c) Evaluate \(\int_3^9 v(t)dt\) and explain what this integral represents. (3 marks)

(d) Calculate the total distance travelled by the graphic from the time it enters the screen to the time it leaves the screen 15 seconds later. (3 marks)

Question 2 (5 marks) [2024 Section 1 Q6]

The graph of \(y = x \sin(\pi x)\) for \(0 \le x \le 1\) is shown below.

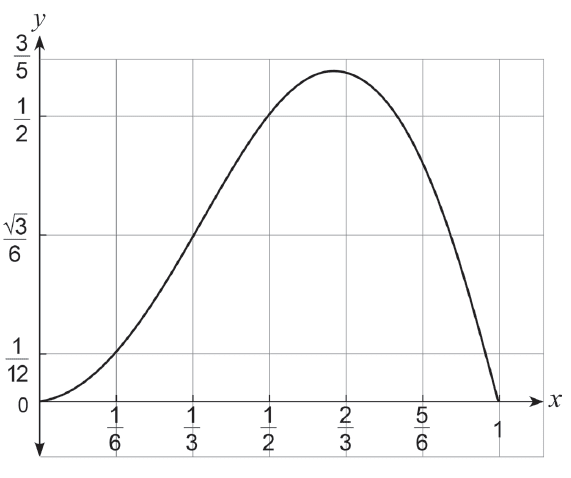
(a) On the diagram above, shade a region whose area is equal to \(\int_{1/6}^{1/2} x \sin(\pi x) dx\). (1 mark)

A spare diagram is provided at the end of this Question/Answer booklet. If you need to use it, cross out this attempt and indicate that you have redrawn it on the spare diagram.

(b)

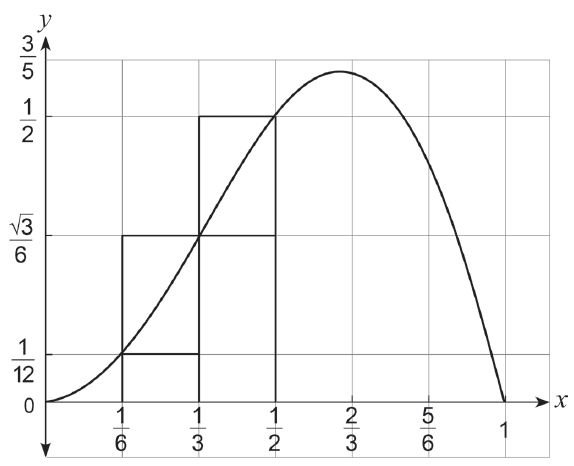
(i) By considering the areas of the rectangles shown in the graph of \(y = x \sin(\pi x)\) above, demonstrate and explain why \[\frac{1 + 2\sqrt{3}}{72} < \int_{1/6}^{1/2} x \sin(\pi x) dx < \frac{3 + \sqrt{3}}{36}\] (3 marks)

(ii) State one suggestion as to how the approximation from part (b)(i) could be improved. (1 mark)

Question 1 (6 marks) [2024 Section 1 Q1]

(a) Differentiate the function \(f(x) = x^2 \ln(4x + 3)\). (2 marks)

(b) Determine a fully simplified expression for \(g(x)\), given that \(g'(x) = \frac{3x}{3x^2 + 1}\) and \(g(1) = \ln(6)\). (4 marks)

Question 1 (13 marks) [2023 Section 1 Q5]

The table below contains values of the polynomial function \(f(x)\), its first and second derivatives, and the function \(F(x) = \int_{0}^{x} f(t)dt\) for \(x = 0, 1, 2, 3, 4, 5, 6\).

\(f(x)\) has no stationary points at non-integer values of \(x\), and the letters \(a, b, c, d\) and \(e\) represent unspecified constants.

(a) Evaluate \( \frac{d}{dx}(f(x)^2) \) when \(x = 2\). (2 marks)

(b) Evaluate \( \int_{2}^{4} (f(x)+2) dx \). (3 marks)

(c) Evaluate \( \frac{d}{dx} \int_{2}^{x} f(t) dt \) when \(x=2\). (2 marks)

(d) Determine the x-coordinate of any stationary points and whether they are local maxima, local minima or inflection points. Justify your answer. (3 marks)

(e) Sketch a possible graph of \(f(x)\) for \(0 \le x \le 6\) on the axes below. (3 marks)

Question 1 (14 marks) [2023 Section 1 Q2]

Let \( p = \ln(2) \), \( q = \ln(3) \) and \( r = \ln(5) \).

(a) Express each of the following in terms of \( p, q \) and/or \( r \).

(i) \( \ln(6) \) (2 marks)

(ii) \( \ln(6.25) \) (3 marks)

(iii) \( \int_{2}^{3} \frac{d}{dx} \ln(x) dx \) (2 marks)

(b) Evaluate \( e^{p+q} \). (2 marks)

(c)

(i) Determine \( \frac{d}{dx}(x \ln(x)) \). (1 mark)

(ii) Hence show that \( \int \ln(x) dx = x \ln(x) - x + c \) where \( c \) is a constant. (2 marks)

(iii) Evaluate \( \int_{1}^{3} \ln(x) dx \) in terms of \( p, q \) and/or \( r \). (2 marks)

Question 1 (8 marks) [2023 Section 1 Q1]

(a) Consider the function \(f(x) = x^3e^{2x}\).

(i) Differentiate \(f(x)\). (2 marks)

(ii) Determine the value of \(x\) for any stationary points of \(f(x)\). (3 marks)

(b) Evaluate \( \int_{0}^{\frac{\pi}{4}} \sin(2x + \pi) dx \). (3 marks)

Question 1 (9 marks) [2022 Section 1 Q1]

Consider the derivative function \( f'(x) = \frac{4x}{x^2 + 3} \).

(a) Determine the rate of change of \(f'(x)\) when \(x = 1\). (3 marks)

(b) Determine \(f(x)\) given that \(f(1) = \ln(32)\). (4 marks)

(c) Determine \( \frac{d}{dt} \int_{t}^{4} f(x) dx \). (2 marks)

Question 2 (6 marks) [2022 Section 1 Q2]

Consider the function \(f(x)\) shown below.

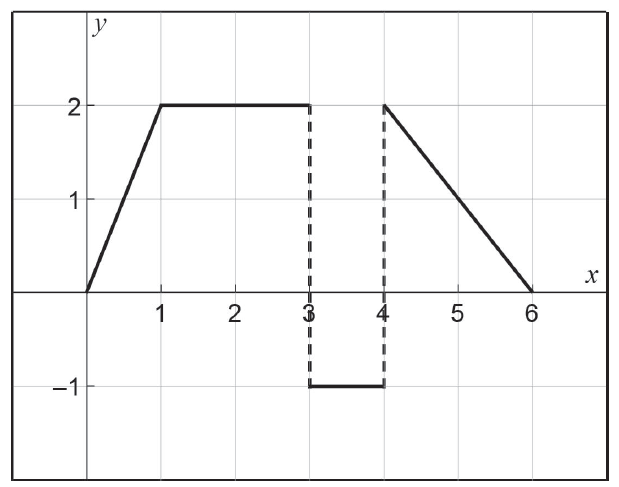
Evaluate the following integrals.

(a) \( \int_{0}^{6} f(x) dx \) (2 marks)

(b) \( \int_{0}^{4} (f(x) - 2) dx \) (2 marks)

(c) \( \int_{4}^{6} f'(x) dx \) (2 marks)

Question 1 (9 marks) [2021 Section 1 Q7]

(a) Consider the function \( f(x) = \frac{1}{x} \), graphed twice below.

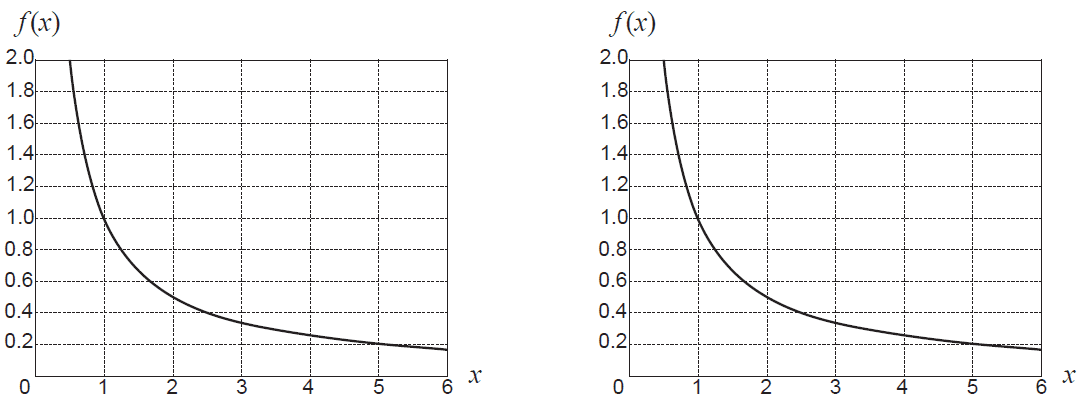
(i) Shade two different regions (one on each graph above) each with area exactly \( \ln(2) \). (2 marks)

(ii) Given that \( \int_{a}^{b} \frac{1}{x} dx = \ln(3) \), what is the relationship between \(a\) and \(b\)? (2 marks)

(b) Another graph of \( f(x) = \frac{1}{x} \) is shown below.

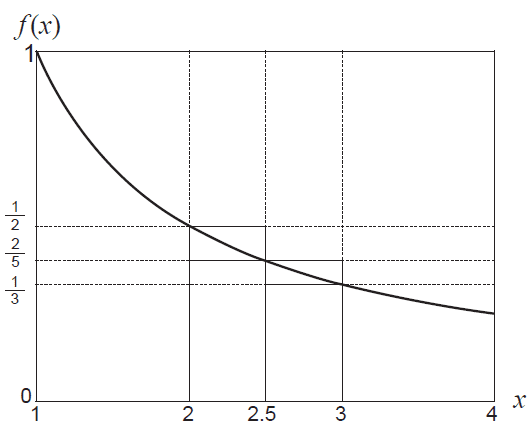
(i) By considering the areas of the rectangles shown, demonstrate and explain why

\[ \frac{11}{30} < \int_{2}^{3} \frac{1}{x} dx < \frac{9}{20} \] (3 marks)

(ii) Hence show that \( \frac{11}{30} < \ln(1.5) < \frac{9}{20} \). (2 marks)

Question 1 (7 marks) [2021 Section 1 Q4]

Determine the following:

(a) \( \int (2x^2 - x^3) dx \) (2 marks)

(b) \( \int_{0}^{\frac{\pi}{3}} \frac{\sin(x)}{3 - \cos(x)} dx \) (3 marks)

(c) \( \frac{d}{dy} \int_{-1}^{y} 3x^2 \cos(2x) dx \) (2 marks)

Question 2 (6 marks) [2021 Section 1 Q5]

(a) Determine the area between the parabola \( y = x^2 - x + 3 \) and the straight line \( y = x + 3 \). (4 marks)

(b) The area between the parabola \( y = x^2 - x - 2 \) and the straight line \( y = x - 2 \) is the same as the area determined in part (a). Explain why this is the case. (2 marks)

Question 1 (6 marks) [2019 Section 1 Q1]

Consider the derivative function \(f'(x) = xe^{x^2}\).

(a) Determine \(f''(1)\). (2 marks)

(b) Explain the meaning of your answer to part (a). (1 mark)

(c) Determine the expression for \(y=f(x)\), given that it intersects the y-axis at the point (0,2). (3 marks)

Question 2 (8 marks) [2019 Section 1 Q5]

(a) Determine the area bound by the graph of \(f(x)=e^x\) and the x-axis between \(x=0\) and \(x=\ln 2\). (3 marks)

(b) Hence, determine the area bound by the graph of \(f(x)=e^x\), the line \(y=2\) and the y-axis. (2 marks)

(c) Determine the area bound by the graph of \(f(x)=e^x\), the line \(y=a\) and the y-axis, where \(a\) is a positive constant. (3 marks)

Question 1 (10 marks) [2018 Section 1 Q7]

(a) Determine a simplified expression for \(\frac{d}{dx}(x\ln(x))\). (2 marks)

(b) Use your answer from part (a) to show that \(\int \ln(x) dx = x\ln(x) - x + c\), where c is a constant. (4 marks)

The graphs of the functions \(f(x)=5\) and \(g(x)=\ln(x)\) are shown below.

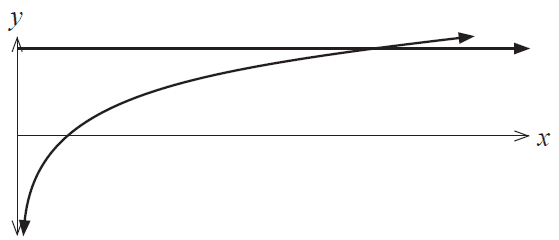
(c) Determine the exact area enclosed between the \(x\) axis, the \(y\) axis and the functions \(f(x)\) and \(g(x)\). (4 marks)

Question 1 (12 marks) [2018 Section 1 Q3]

(a) Differentiate \((2x^3+1)^5\). (2 marks)

(b) Given \(g'(x) = e^{2x}\sin(3x)\), determine a simplified value for the rate of change of \(g'(x)\) when \(x=\frac{\pi}{2}\). (3 marks)

(c) Determine the following:

(i) \(\int 3\cos(2x) dx\). (2 marks)

(ii) \(\int_0^1 \frac{3x+1}{3x^2+2x+1} dx\). (3 marks)

(d) If \(f'(x) = e^{-2x}\), find the expression for \(y=f(x)\), given \(f(0)=-2\). (2 marks)

Question 1 (5 marks) [2017 Section 1 Q8]

(a) Differentiate \(2x\sin(3x)\) with respect to \(x\). (2 marks)

(b) Hence show that \(\int x \cos(3x) dx = \frac{3x \sin(3x) + \cos(3x)}{9} + c\). (3 marks)

Question 2 (8 marks) [2017 Section 1 Q9]

Consider the function \(f(x)\) shown graphed below. The table gives the value of the function at the given \(x\) values.

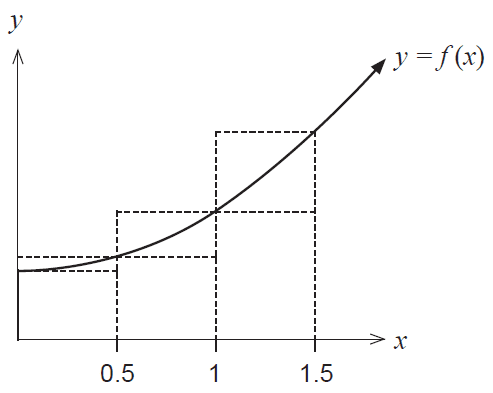
\(x\)	0	0.5	1	1.5
\(f(x)\)	20	21	24	29

(a) By considering the areas of the rectangles shown, demonstrate and explain why

\[ 32.5 < \int_0^{1.5} f(x) dx < 37 \] (3 marks)

Consider the table of further values of \(f(x)\) given below.

\(x\)	0	0.5	1	1.5	2	2.5	3
\(f(x)\)	20	21	24	29	36	45	56

(b) Use the table values to determine the best estimate possible for \(\int_1^3 f(x)dx\). (3 marks)

(c) State two ways in which you could determine a more accurate value for \(\int_1^3 f(x)dx\). (2 marks)

Question 1 (8 marks) [2017 Section 1 Q5]

(a) Consider the shaded area shown between the graph of \(y=e^x\), the y axis and the line \(y=2\).

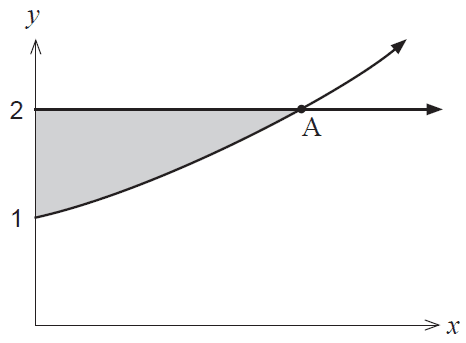
(i) Determine the coordinates of the point A. (1 mark)

(ii) Hence or otherwise determine the area between the graph of \(y=e^x\), the y axis and the line \(y=2\). (3 marks)

(b) If the area between the graph of \(y=e^x\), the y axis, the x axis and the line \(x=k\), where \(k \ge 0\), is to be equal to 2 square units, determine the exact value of \(k\). (4 marks)

Question 2 (7 marks) [2017 Section 1 Q6]

(a) Evaluate \(\int_{0}^{1} \frac{-12x}{1+3x^2} dx\). (3 marks)

(b) Given \(f(x) = \ln(2-x^3)\)

(i) determine \(f'(1)\). (3 marks)

(ii) In relation to the graph of \(f(x)\), explain the meaning of your answer to (b)(i). (1 mark)