WACE Maths Methods ATAR Paper 1 Topic Tests
Logarithmic Function Topic Test 1
Section One: Technology-free
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The function \(f(x) = \log_a(x)\) is plotted below, where \(a\) and \(p\) are constants.
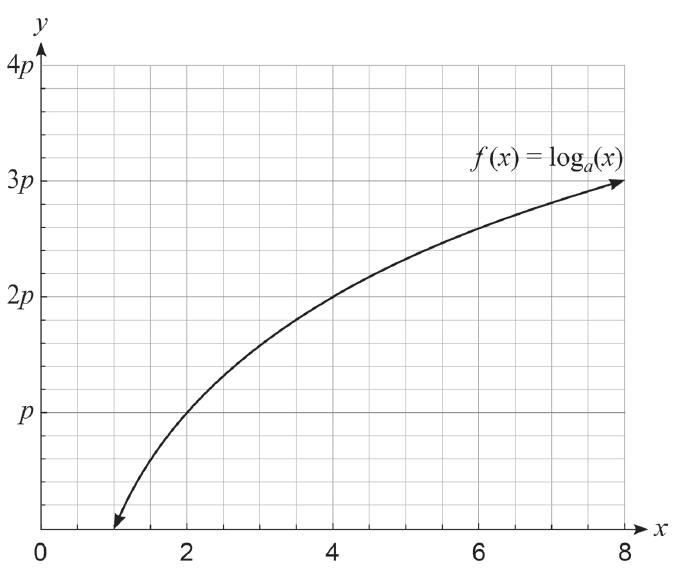
(a) Express \(\log_a(0.5)\) in terms of \(p\). (2 marks)
(b) Evaluate \(a^{5p}\). (2 marks)
(c) Solve \(\log_a(x-3) = 3p\) for \(x\). (2 marks)
The function \(f(x) = \log_a(x)\) has been transformed to give two other logarithmic functions with base \(a\) on the axes as shown below.
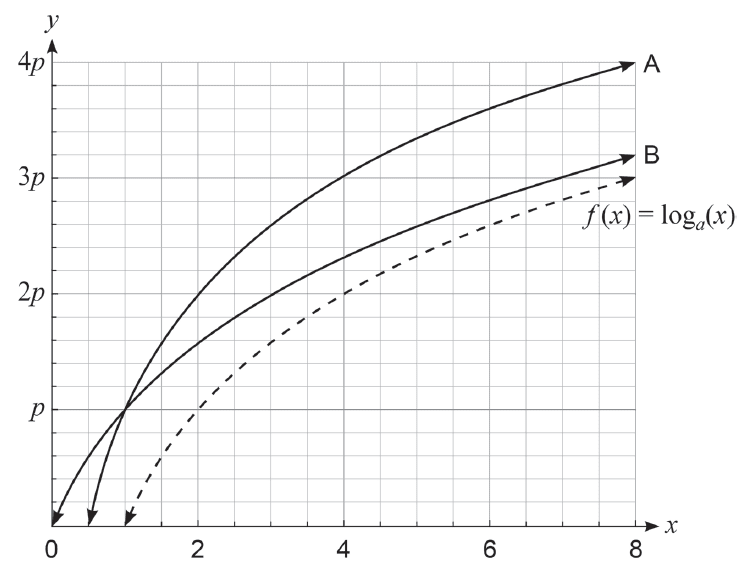
(d) Determine an equation for each of the two functions, A and B. (2 marks)
End of questions
Logarithmic Function Topic Test 2
Section One: Technology-free
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
An internet search engine uses a logarithmic scale to rank the importance of internet websites. If a website has \(S\) visits each week, the site rank, \(R\), is given by \[ R = 2\log_{10}\left(\frac{S}{S_0}\right) \] where \(S_0\) is the reference value (the same for all websites). The reference value is the minimum number of visits per week required for a website to register on the site rank scale.
(a) Determine the site rank for a website whose weekly visits are one hundred times the reference value. (2 marks)
(b) Given that a site rank of 12 is assigned to a website with 1.5 billion (\(1.5 \times 10^9\)) visits per week, determine the value of \(S_0\). (3 marks)
(c) The plot of \(y = \log_{10}(x)\) is shown below. If a website has a site rank of 3.2, use the plot and your answer from part (b) to approximate the website's number of weekly visits. (3 marks)
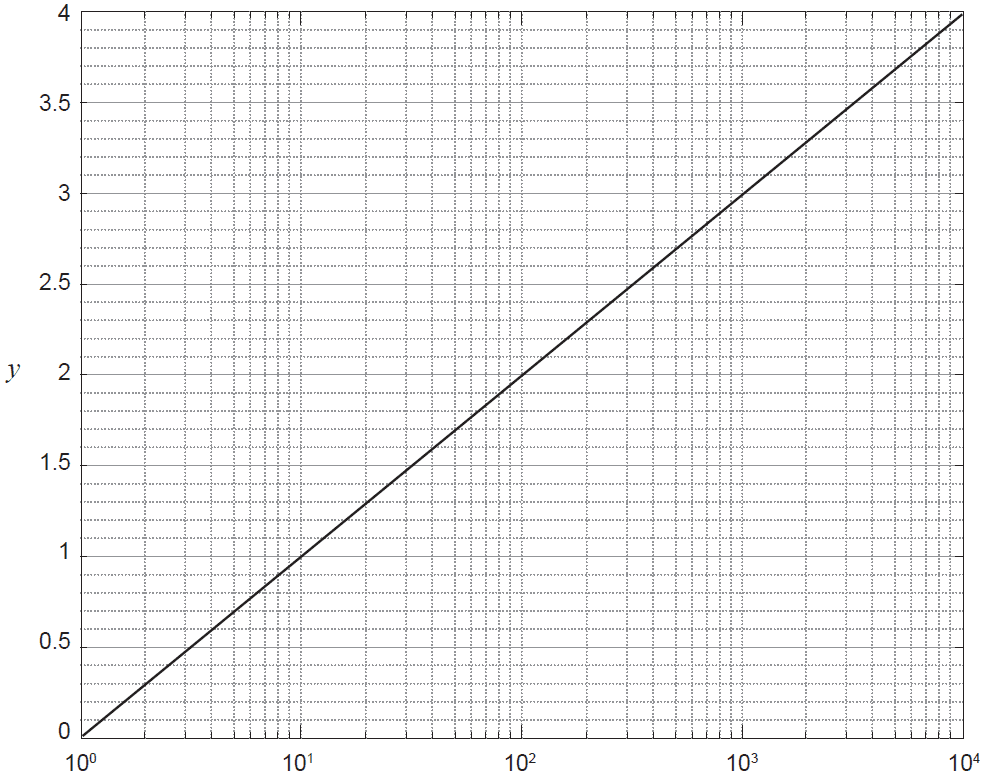
End of questions
Logarithmic Function Topic Test 3
Section One: Technology-free
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The graph of the function \(f(x) = \log_2(x)\) is shown below.
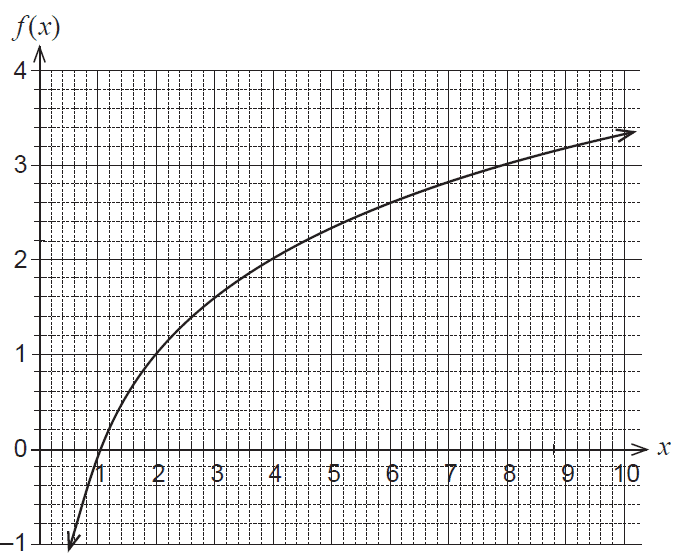
(a) Using the graph:
(i) solve \( \log_2(x-5) = 3 \). (2 marks)
(ii) determine \( \sqrt{7} \), correct to one decimal place. (Hint: let \(x = \sqrt{7}\).) (3 marks)
(b) The function \(f(x) = \log_2(x)\) is translated to give the new function \(g(x)\), which is shown in the graph below.
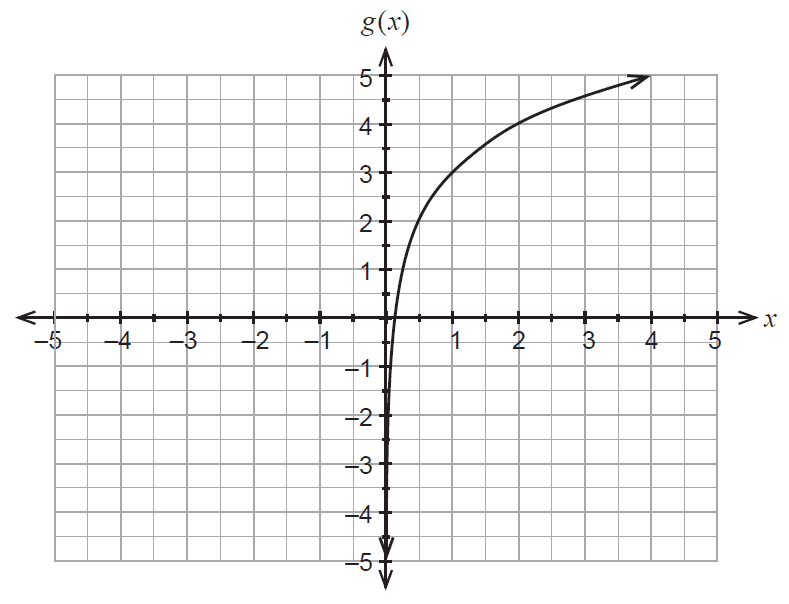
Determine the equation for \(g(x)\). (2 marks)
(c)
(i) Show that \( \log_2 \left(\frac{1}{x-1}\right) = -\log_2(x-1) \). (2 marks)
(ii) Hence sketch the graph of \( h(x) = \log_2 \left(\frac{1}{x-1}\right) \) on the axes below. (3 marks)
End of questions
Logarithmic Function Topic Test 4
Section One: Technology-free
Number of marks: 12
Reading time: 1 minute
Writing time: 12 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Consider the graph of \(y=\ln(x)\) shown below.
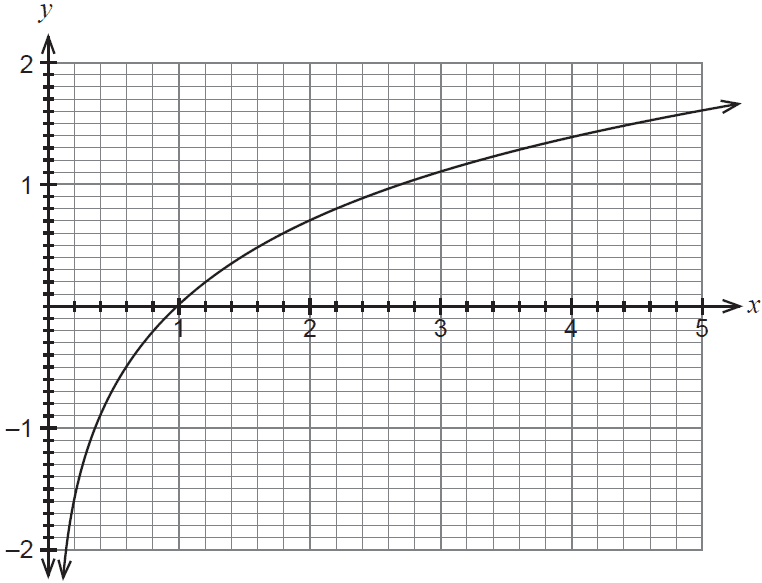
(a) Use the graph to estimate the value of \(p\) in each of the following.
(i) \(1.4 = \ln(p)\) (1 mark)
(ii) \(e^{p+1}-3=0\) (2 marks)
(b) On the axes below, sketch the graph of \(y = \ln(x-2)+1\). (3 marks)
Consider the function \(f(x) = \ln(x)\). The function \(g(x) = f(x) + a\) is a vertical translation of \(f\) by \(a\) units.
(a) Express the function \(g(x) = \ln(4x)\) in terms of a vertical translation of \(f\) (i.e. in the form \(g(x) = f(x) + a\)), stating the number of units that \(f\) is translated. (2 marks)
The function \(h(x) = cf(x)\) is a vertical dilation of \(f\) by a scale factor of \(c\).
(b) Express the function \(h(x) = \ln(\sqrt{x})\) in terms of a vertical dilation of \(f\), stating the scale factor. (2 marks)
The function \(p(x) = f(bx)\) is a horizontal dilation of \(f\) by a scale factor of \( \frac{1}{b} \).
(c) Express the function \(p(x) = \ln(x) + 4\) in terms of a horizontal dilation of \(f\), stating the scale factor. (3 marks)
End of questions
Logarithmic Function Topic Test 5
Section One: Technology-free
Number of marks: 10
Reading time: 1 minute
Writing time: 10 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Solve \(4e^{2x} = 81 - 5e^{2x}\) exactly for \(x\).
Given that \(\log_{10}2 = x\) and \(\log_{10}7 = y\)
(a) express \(\log_{10}14\) in terms of \(x\) and \(y\). (2 marks)
(b) show that \(\log_{10}17.5 = y - 2x + 1\). (2 marks)
(c) evaluate \(10^{y-x}\). (2 marks)
End of questions



