WACE Maths Methods ATAR Paper 1 Topic Tests
Differential Calculus Topic Test 1
Section One: Technology-free
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Given that \( \ln(2) \approx 0.693 \), use the increments formula to determine an approximation for \( \ln(2.02) \).
A continuous function, \(f\), satisfies the following conditions:
- \(f(2) = 0\)
- \(f\) has exactly 2 stationary points
- \(f'(-1) = 0\) and \(f'(1) = 0\)
- \(f''(-1) = 4\)
- \(f'(2) > 0\).
Sketch the function on the axes below.
End of questions
Differential Calculus Topic Test 2
Section One: Technology-free
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Consider the function \(f(x) = e^{2x} - 4e^x\).
(a) Determine the coordinates of the x-intercept(s) of \(f\). You may wish to consider the factorised version of \(f: f(x) = e^x(e^x - 4)\). (3 marks)
(b) Show that there is only one turning point on the graph of \(f\), which is located at \((\ln(2), -4)\). (3 marks)
(c) Determine the coordinates of the point(s) of inflection of \(f\). (3 marks)
(d) Sketch the function \(f\) on the axes below, labelling clearly all intercepts, the turning point and point(s) of inflection. Some approximate values of the natural logarithmic function provided in the table below may be helpful. (4 marks)
| \(x\) | 1 | 2 | 3 | 4 |
| \(\ln(x)\) | 0 | 0.7 | 1.1 | 1.4 |
End of questions
Differential Calculus Topic Test 3
Section One: Technology-free
Number of marks: 5
Reading time: 1 minute
Writing time: 5 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The graphs of the functions \(f\) and \(g\) are displayed below.
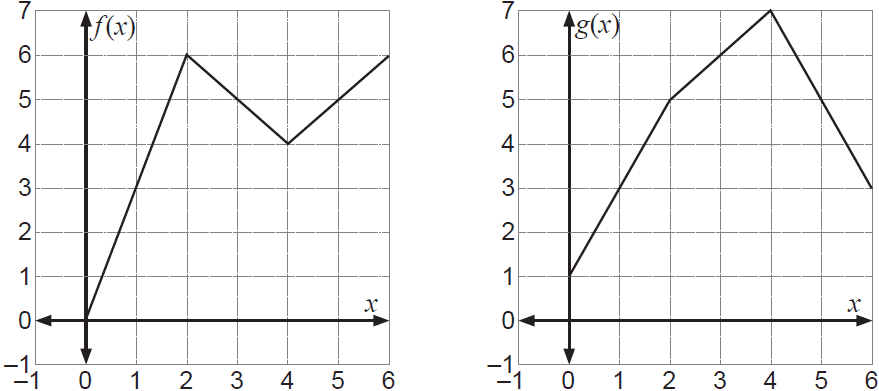
(a) Evaluate the derivative of \(f(x)\) at \(x = 3\). (1 mark)
(b) Evaluate the derivative of \(f(x)g(x)\) at \(x = 5\). (2 marks)
(c) Evaluate the derivative of \(f(g(x))\) at \(x = 1\). (2 marks)
End of questions
Differential Calculus Topic Test 4
Section One: Technology-free
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A company's profit, in millions of dollars, over a five-year period can be modelled by the function: \(P(t) = 2t\sin(3t)\) \(0 \le t \le 5\) where \(t\) is measured in years.
The graph of \(P(t)\) is shown below.
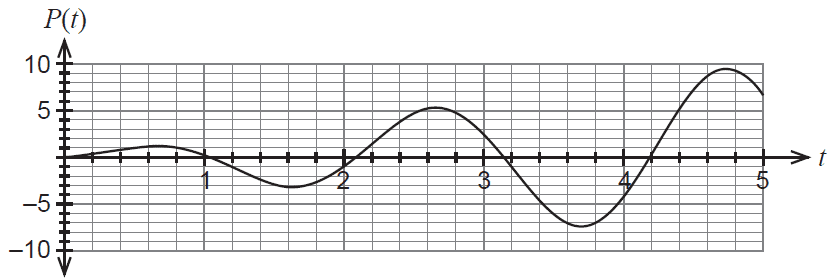
(a) Differentiate \(P(t)\) to determine the marginal profit function, \(P'(t)\). (2 marks)
(b) Calculate the rate of change of the marginal profit function when \(t = \frac{\pi}{18}\) years. (4 marks)
(c) Use the increments formula at \(t = \frac{7\pi}{6}\) to estimate the change in profit for a one month change in time. (3 marks)
If \( h(x) = \frac{e^{-x}}{\cos x} \), then evaluate \( h'(\pi) \).
End of questions
Differential Calculus Topic Test 5
Section One: Technology-free
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A company manufactures and sells an item for $\(x\). The profit, $\(P\), made by the company per item sold is dependent on the selling price and can be modelled by the function:
\[ P(x) = \frac{50 \ln\left(\frac{x}{2}\right)}{x^2} \text{ where } 1.5 \le x \le 10 \]The graph of \(P(x)\) is shown below:
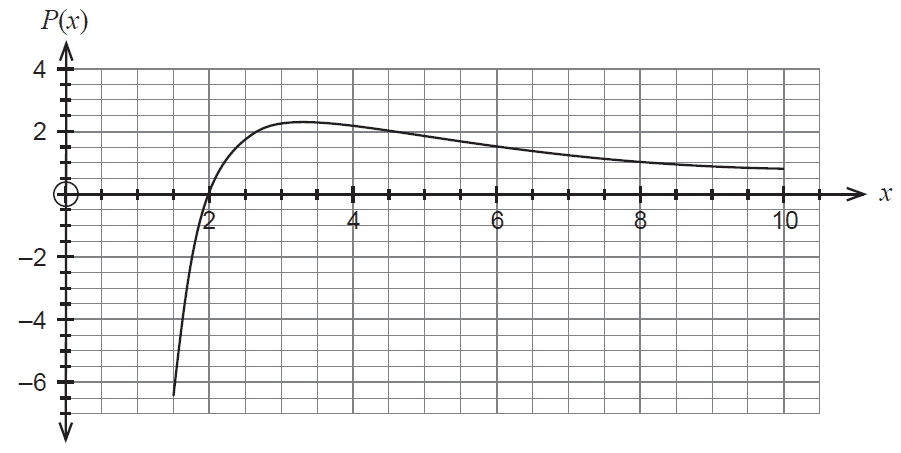
(a) Describe how the profit per item sold varies as the selling price changes. (3 marks)
(b) Determine the exact price that should be charged for the item if the company wishes to maximise the profit per item sold. (5 marks)
The values of the functions \(g(x)\) and \(h(x)\), and their derivatives \(g'(x)\) and \(h'(x)\) are provided in the table below for \(x=1\), \(x=2\) and \(x=3\).
| \(x=1\) | \(x=2\) | \(x=3\) | |
|---|---|---|---|
| \(g(x)\) | 3 | 5 | -3 |
| \(h(x)\) | 2 | -2 | 6 |
| \(g'(x)\) | -4 | 1 | 4 |
| \(h'(x)\) | 0 | -6 | -5 |
(a) Evaluate the derivative of \(\frac{g(x)}{h(x)}\) at \(x=3\). (2 marks)
(b) Evaluate the derivative of \(h(g(x))\) at \(x=1\). (2 marks)
(c) If \(h''(1) = -1\), describe with justification, what the graph of \(h(x)\) looks like at this point. (2 marks)
End of questions
Differential Calculus Topic Test 6
Section One: Technology-free
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A bicycle rolls down a ramp from an initial height of 5.15 m as shown in the diagram below.
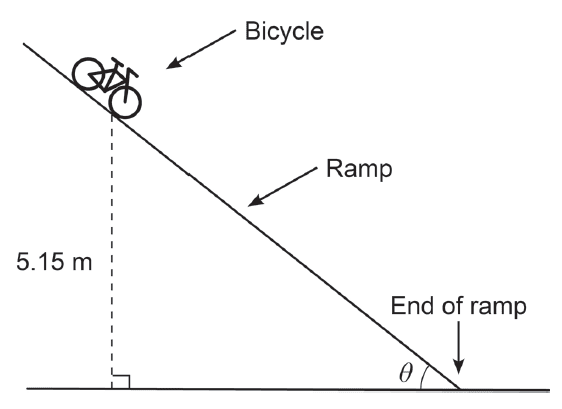
The speed, \(s\), of the bicycle (in metres per second) when it reaches the end of the ramp is given by \[s(\theta) = \sqrt{\frac{101 \sin(\theta) - \cos(\theta)}{\sin(\theta)}}\] where \(\theta\) (in radians) is the ramp angle shown in the diagram.
(a) Determine the speed of the bicycle at the end of the ramp, if the ramp angle is 45°. (2 marks)
(b) Determine \(\frac{d}{d\theta}\left(\frac{101 \sin(\theta) - \cos(\theta)}{\sin(\theta)}\right)\). Simplify your answer. (3 marks)
(c) Hence, show that \(\frac{ds}{d\theta} = \frac{1}{2\sin^2(\theta)} \frac{\sin(\theta)}{\sqrt{101\sin(\theta)-\cos(\theta)}}\). (2 marks)
(d) Use the increments formula to estimate the change in \(s\) if the ramp angle is changed from 45° to 46°. (3 marks)
End of questions


