2019 VCE Maths Methods Mini Test 11
Number of marks: 8
Reading time: 1 minute
Writing time: 12 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The weights of packets of lollies are normally distributed with a mean of 200 g.
If 97% of these packets of lollies have a weight of more than 190 g, then the standard deviation of the distribution, correct to one decimal place, is
- A. 3.3 g
- B. 5.3 g
- C. 6.1 g
- D. 9.4 g
- E. 12.1 g
Let \(f: [2, \infty) \to R, f(x) = x^2 - 4x + 2\) and \(f(5) = 7\). The function \(g\) is the inverse function of \(f\).
\(g'(7)\) is equal to
- A. \(\frac{1}{6}\)
- B. 5
- C. \(\frac{\sqrt{7}}{14}\)
- D. 6
- E. \(\frac{1}{7}\)
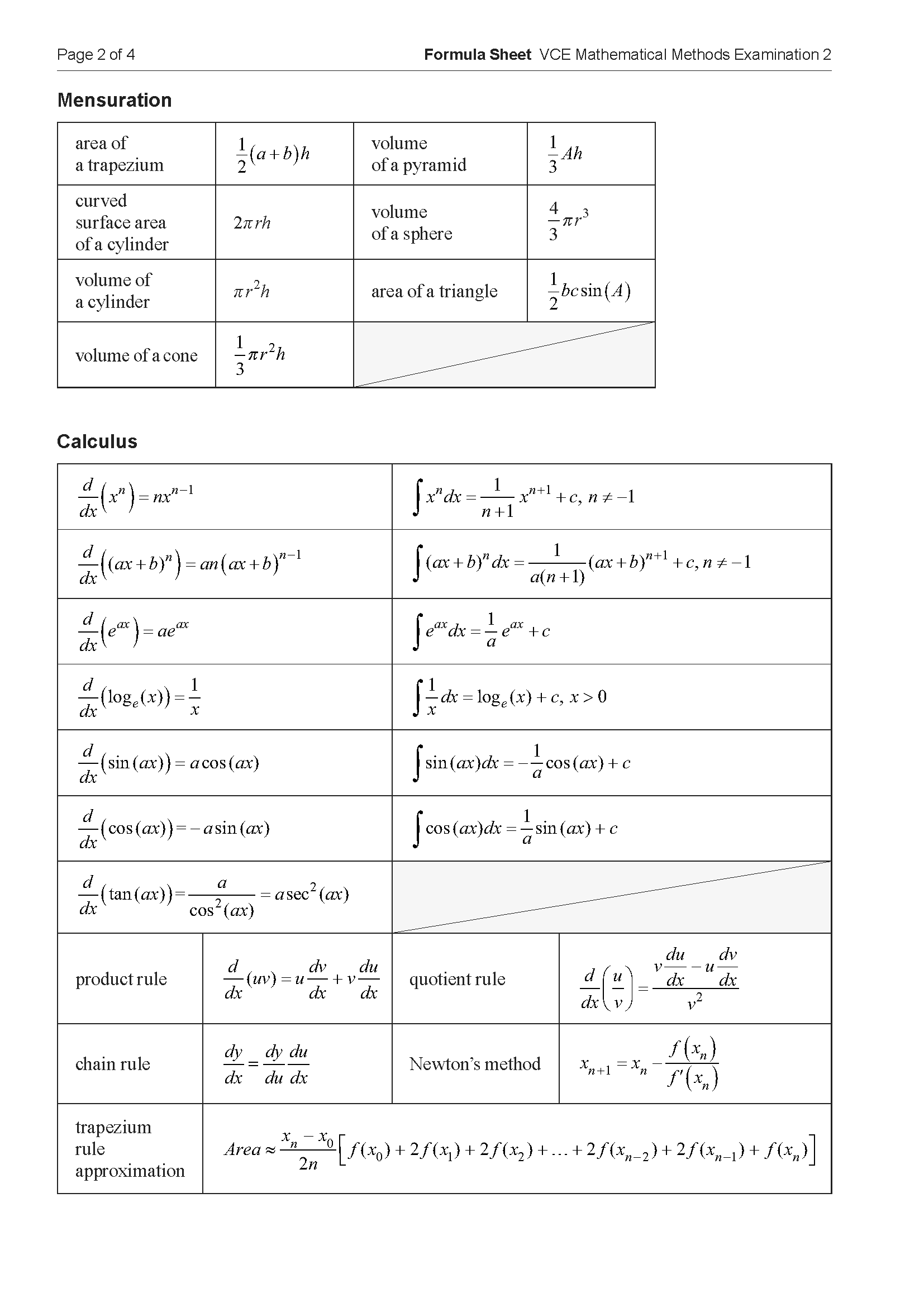
Part of the graph of \(y = f(x)\) is shown below.
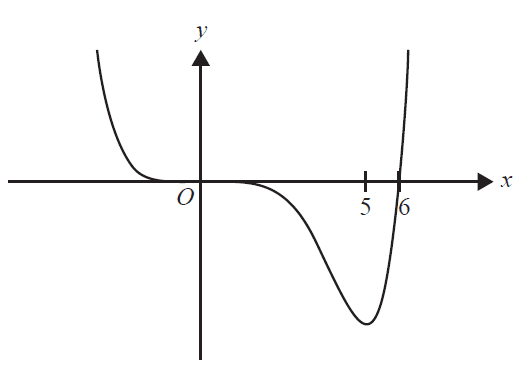
The corresponding part of the graph of \(y = f'(x)\) is best represented by
A box contains \(n\) marbles that are identical in every way except colour, of which \(k\) marbles are coloured red and the remainder of the marbles are coloured green. Two marbles are drawn randomly from the box.
If the first marble is not replaced into the box before the second marble is drawn, then the probability that the two marbles drawn are the same colour is
- A. \(\frac{k^2 + (n-k)^2}{n^2}\)
- B. \(\frac{k^2 + (n-k-1)^2}{n^2}\)
- C. \(\frac{2k(n-k-1)}{n(n-1)}\)
- D. \(\frac{k(k-1) + (n-k)(n-k-1)}{n(n-1)}\)
- E. \(^nC_2\left(\frac{k}{n}\right)^2\left(1-\frac{k}{n}\right)^{n-2}\)
The distribution of a continuous random variable, \(X\), is defined by the probability density function \(f\), where
\(f(x) = \begin{cases} p(x) & -a \le x \le b \\ 0 & \text{otherwise} \end{cases}\)
and \(a, b \in R^+\).
The graph of the function \(p\) is shown below.
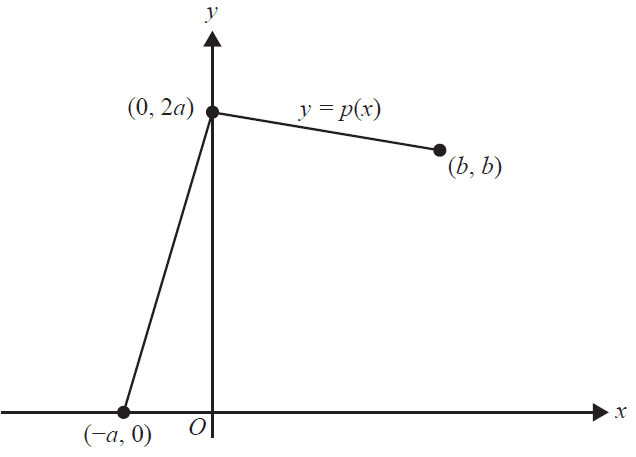
It is known that the average value of \(p\) over the interval \([-a, b]\) is \(\frac{3}{4}\).
\(\Pr(X>0)\) is
- A. \(\frac{2}{3}\)
- B. \(\frac{3}{4}\)
- C. \(\frac{4}{5}\)
- D. \(\frac{7}{9}\)
- E. \(\frac{5}{6}\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The function \(f: \mathbb{R} \to \mathbb{R}\), \(f(x)\) is a polynomial function of degree 4. Part of the graph of \(f\) is shown below.
The graph of \(f\) touches the \(x\)-axis at the origin.
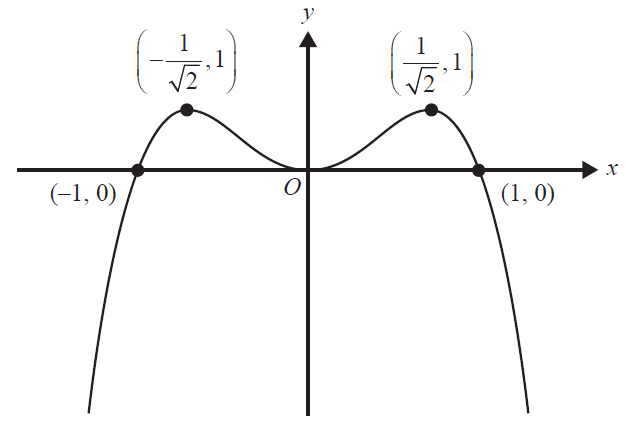
a. Find the rule of \(f\). 1 mark
Let \(g\) be a function with the same rule as \(f\).
Let \(h: D \to \mathbb{R}\), \(h(x) = \log_e(g(x)) - \log_e(x^3+x^2)\), where \(D\) is the maximal domain of \(h\).
b. State \(D\). 1 mark
c. State the range of \(h\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au