WACE Maths Methods ATAR Section 2 Topic Tests
Logarithmic Function Topic Test 1
Section Two: Technology-active
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Earthquake magnitude can be measured using the moment magnitude scale (\(M_w\)), which is related to the seismic moment \(M_0\) of an earthquake. The seismic moment has units of Nm. The graph of \(M_w\) versus \(\log_{10}(M_0)\) is given below.

(a) Use the graph to approximate the moment magnitude \(M_w\) of an earthquake with a seismic moment of \(3.16 \times 10^{13}\) Nm. You must show clearly how you have used the graph. (2 marks)
(b) The relationship between \(M_w\) and \(M_0\) can be expressed in the form \[ M_w = a\log_{10}(M_0) + b. \] Determine the values of \(a\) and \(b\). (2 marks)
(c) Hence, or otherwise, express the relationship between \(M_w\) and \(M_0\) in the form \[ M_w = a \log_{10}\left(\frac{M_0}{c}\right). \] (3 marks)
(d) Determine the seismic moment, \(M_0\), of an earthquake with moment magnitude \(M_w = 4\). (2 marks)
The graph of \( y = m\log_3(x-p) + q \) has a vertical asymptote at \( x = 5 \).
(a) Explain why \(p = 5\). (2 marks)
(b) If this graph passes through the points (6, 2) and (14, -6), determine the values of \(m\) and \(q\). (2 marks)
End of questions
Logarithmic Function Topic Test 2
Section Two: Technology-active
Number of marks: 7
Reading time: 1 minute
Writing time: 7 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The ear has the remarkable ability to handle an enormous range of sound levels. In order to express levels of sound meaningfully in numbers that are more manageable, a logarithmic scale is used, rather than a linear scale. This scale is the decibel (dB) scale.
The sound intensity level, \(L\), is given by the formula below:
\[ L = 10 \log_{10}\left(\frac{I}{I_0}\right) \text{ dB where } I \text{ is the sound intensity and } I_0 \text{ is the reference sound intensity.} \]
\(I\) and \(I_0\) are measured in watt/m².
(a) Listening to a sound intensity of 5 billion times that of the reference intensity (\(I=5\times 10^9 I_0\)) for more than 30 minutes is considered unsafe. To what sound intensity level does this correspond? (2 marks)
(b) The reference sound intensity, \(I_0\), has a sound intensity level of 0 dB. If a household vacuum cleaner has a sound intensity \(I = 1 \times 10^{-5}\) watt/m² and this corresponds to a sound intensity level \(L=70\) dB, determine \(I_0\). (2 marks)
The average sound intensity level for rainfall is 50 dB and for heavy traffic 85 dB.
(c) How many times more intense is the sound of traffic than that of rainfall? (3 marks)
End of questions
Logarithmic Function Topic Test 3
Section Two: Technology-active
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The volume \(V(h)\) in cubic metres of a liquid in a large vessel depends on the height \(h\) (metres) of the liquid in the vessel and is given by
\[ V(h) = \int_0^h e^{\frac{x^2}{100}} dx, \quad 0 \le h \le 15. \]
(a) Determine \(\frac{dV}{dh}\) when the height is 0.5 m. (2 marks)
(b) What is the meaning of your answer to part (a)? (1 mark)
(c) The height of the liquid depends on time \(t\) (seconds) as follows: \(h(t) = 3t^2 - t + 4, t \ge 0\).
(i) Determine \(\frac{dh}{dt}\) when the height is 6 m. (2 marks)
(ii) Use the chain rule to determine \(\frac{dV}{dt}\) when the height is 6 m. (2 marks)
(iii) Given the volume of the liquid at 2 seconds is 8.439 m³, use the incremental formula to estimate the volume 0.1 second later. (3 marks)
End of questions
Logarithmic Function Topic Test 4
Section Two: Technology-active
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The intensity of light travelling through a medium decreases due to scattering and absorption. The intensity of light, \(I\), after travelling a distance of \(x\) centimetres through a soft tissue sample is given by
\[ I = I_0 e^{-0.75x} \]
where \(I_0\) is the initial light intensity.
(a) What percentage of the initial light intensity remains after the light has travelled 1 cm through the soft tissue? (2 marks)
(b) After how many centimetres will the light intensity have reached one quarter of its initial value? (2 marks)
(c) Determine an expression for \(\ln\left(\frac{I}{I_0}\right)\) and hence plot \(\ln\left(\frac{I}{I_0}\right)\) versus \(x\) on the axes below. (3 marks)
The intensity of light passing through a different type of soft tissue satisfies the equation
\[ I = I_0 e^{-\mu x} \]where \(\mu\) is the attenuation constant. Light intensity measurements were made on a sample of soft tissue, and the results plotted in the graph below.
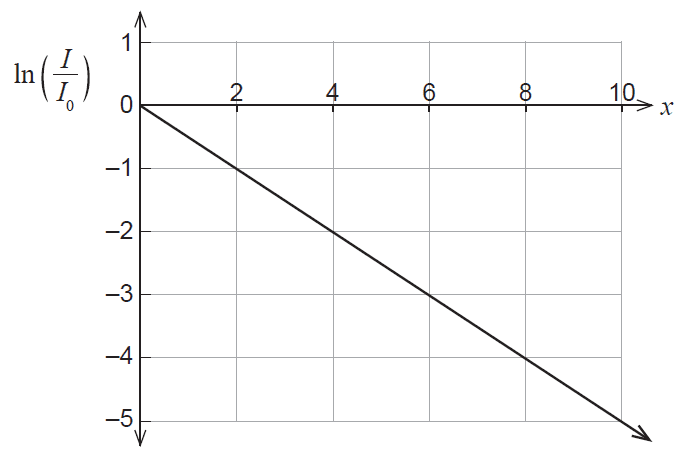
(d) Use the graph to determine the value of the attenuation constant, \(\mu\). (1 mark)
(e)
(i) Express the equation \(I = I_0 e^{-0.75x}\) using base 10 (in the form \(I = I_0 10^{-bx}\)). State the value of \(b\) to three decimal places. (3 marks)
(ii) Describe the change in intensity over a distance of \(\frac{1}{b}\) cm. (2 marks)
End of questions
Logarithmic Function Topic Test 5
Section Two: Technology-active
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A company manufactures small machine components. They can manufacture up to 200 of a particular component in one day. The total cost, in hundreds of dollars, incurred in manufacturing the components is given by: \( C(x) = \frac{x \ln(2x+1)}{3} - 2x + 120 \), where \(x\) is the number of components that will be produced on that day.
(a) Determine the total cost of manufacturing 20 components in one day. (1 mark)
(b) On the axes below, sketch the graph of \(C(x)\). (3 marks)
(c) With reference to your graph in part (b), explain how many components the company should manufacture per day if the total cost is to be as low as possible. (3 marks)
Speed cubers are people who try to solve the Rubik's cube as quickly as possible by using pre-learned algorithms (sequences of turns). Knowing more algorithms has the potential to result in faster solution times. A speed cuber aims to learn the full ZBLL algorithm set, consisting of 493 algorithms.
Assume that the total number of ZBLL algorithms learnt, \(A\), can be modelled by the equation \[ A(t) = b\log_4(t+1) + c \] where \(t\) is the time in weeks since learning commenced, and \(b\) and \(c\) are constant parameters.
(a) Determine the parameters \(b\) and \(c\), given that the speed cuber already knows 21 of the ZBLL algorithms (at \(t = 0\)) and learnt an additional 32 algorithms by the end of the first week. (3 marks)
(b) Determine how many of the ZBLL algorithms the speed cuber will have learnt after 26 weeks. (1 mark)
(c) Based on the assumed model, will the speed cuber learn the entire ZBLL algorithm set within their lifetime? Justify your answer. (2 marks)
End of questions
Logarithmic Function Topic Test 6
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Consider the function \(f(x) = \log_a(x-1)\) where \(a > 1\).
(a) On the axes below, sketch the graph of \(f(x)\), labelling important features. (3 marks)
(b) Determine the value of \(m\) if \(f(m)=1\). (2 marks)
(c) Determine the coordinates of the \(x\)-intercept of \(f(x+b)+c\), where \(b\) and \(c\) are positive real constants. (3 marks)
End of questions


