VCE Maths Methods Trigonometry Mini Test 4
Number of marks: 10
Reading time: 2 minutes
Writing time: 15 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Let \(f: R \to R, f(x) = 5\sin(2x) - 1\).
The period and range of this function are respectively
- A. \(\pi\) and \([-1, 4]\)
- B. \(2\pi\) and \([-1, 5]\)
- C. \(\pi\) and \([-6, 4]\)
- D. \(2\pi\) and \([-6, 4]\)
- E. \(4\pi\) and \([-6, 4]\)
A clock has a minute hand that is 10 cm long and a clock face with a radius of 15 cm, as shown below.
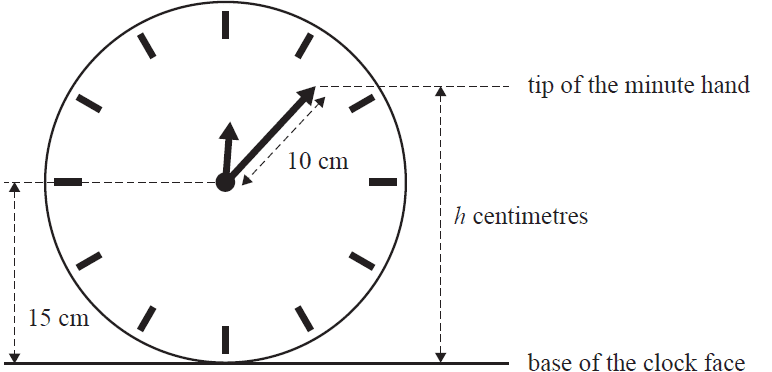
At 12.00 noon, both hands of the clock point vertically upwards and the tip of the minute hand is at its maximum distance above the base of the clock face.
The height, \(h\) centimetres, of the tip of the minute hand above the base of the clock face \(t\) minutes after 12.00 noon is given by
- A. \(h(t) = 15 + 10\sin\left(\frac{\pi t}{30}\right)\)
- B. \(h(t) = 15 - 10\sin\left(\frac{\pi t}{30}\right)\)
- C. \(h(t) = 15 + 10\sin\left(\frac{\pi t}{60}\right)\)
- D. \(h(t) = 15 + 10\cos\left(\frac{\pi t}{60}\right)\)
- E. \(h(t) = 15 + 10\cos\left(\frac{\pi t}{30}\right)\)
Given that \(\tan(a) = d\), where \(d > 0\) and \(0 < a < \frac{\pi}{2}\), the sum of the solutions to \(\tan(2x) = d\), where \(0 < x < \frac{5\pi}{4}\), in terms of \(a\), is
- A. 0
- B. \(2a\)
- C. \(\pi + 2a\)
- D. \(\frac{\pi}{2} + a\)
- E. \(\frac{3(\pi+a)}{2}\)
Consider the graph of the function defined by \(f: [0, 2\pi] \to R, f(x) = \sin(2x)\).
The square of the length of the line segment joining the points on the graph for which \(x = \frac{\pi}{4}\) and \(x = \frac{3\pi}{4}\) is
- A. \(\frac{\pi^2+16}{4}\)
- B. \(\pi+4\)
- C. 4
- D. \(\frac{3\pi^2+16\pi}{4}\)
- E. \(\frac{10\pi^2}{16}\)
Let \(f: R \to R, f(x) = \cos(ax)\), where \(a \in R\setminus\{0\}\), be a function with the property \(f(x) = f(x+h)\), for all \(h \in Z\).
Let \(g: D \to R, g(x) = \log_2(f(x))\) be a function where the range of \(g\) is \([-1, 0]\).
A possible interval for \(D\) is
- A. \(\left[-\frac{1}{4}, \frac{5}{12}\right]\)
- B. \(\left[1, \frac{7}{6}\right]\)
- C. \(\left[-\frac{5}{3}, 2\right]\)
- D. \(\left[-\frac{1}{3}, 0\right]\)
- E. \(\left[-\frac{1}{12}, \frac{1}{4}\right]\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Let \( f: [0, 2\pi] \rightarrow \mathbb{R}, f(x) = 2\cos(x) + 1 \).
a. Solve the equation \( 2\cos(x) + 1 = 0 \) for \( 0 \le x \le 2\pi \). 2 marks
b. Sketch the graph of the function \(f\) on the axes below. Label the endpoints and local minimum point with their coordinates. 3 marks
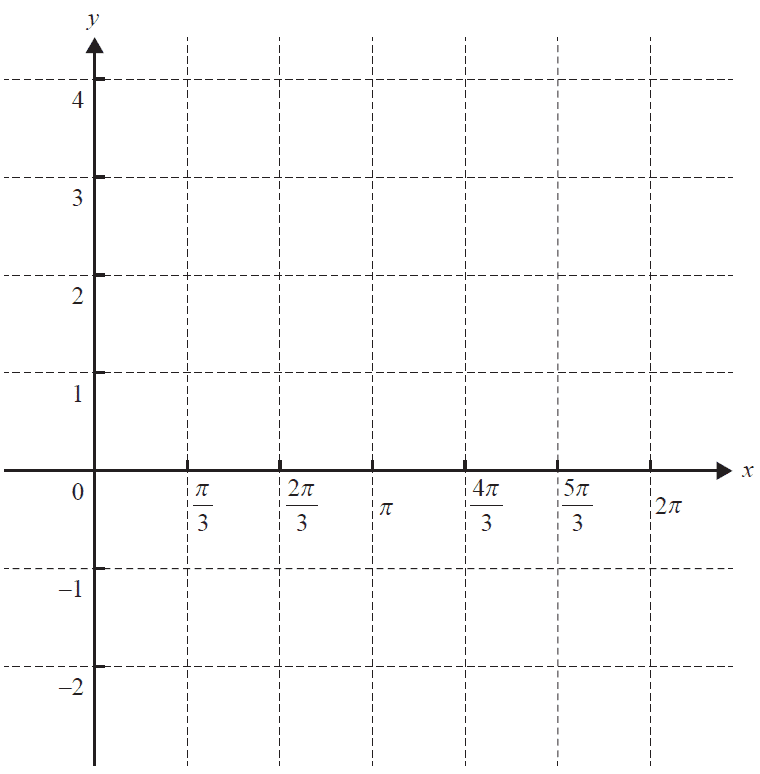
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au