VCE Maths Methods Integral Calculus Mini Test 11
Number of marks: 10
Reading time: 2 minutes
Writing time: 15 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Consider the graphs of the functions \(f\) and \(g\) shown below.
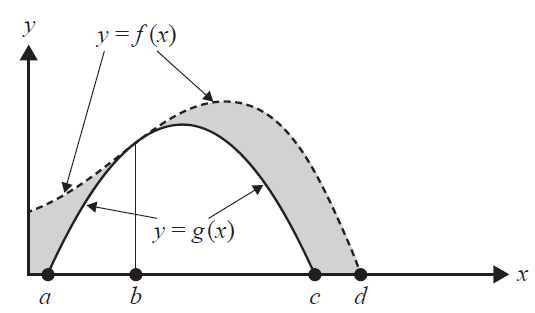
The area of the shaded region could be represented by
- A. \(\int_a^d (f(x)-g(x))dx\)
- B. \(\int_0^d (f(x)-g(x))dx\)
- C. \(\int_0^b (f(x)-g(x))dx + \int_b^c (f(x)-g(x))dx\)
- D. \(\int_0^a f(x)dx + \int_a^c (f(x)-g(x))dx+\int_b^d f(x)dx \)
- E. \(\int_0^d f(x)dx - \int_a^c g(x)dx\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The graph of \(f: [0, 1] \to R, f(x) = \sqrt{x}(1-x)\) is shown below.
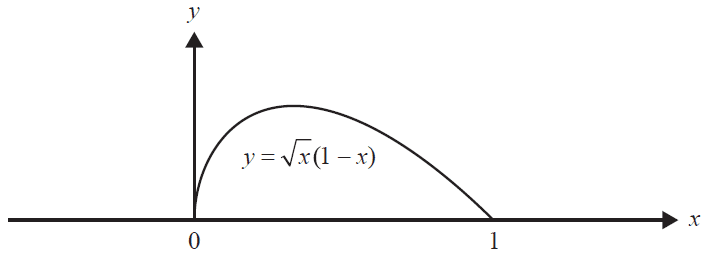
a. Calculate the area between the graph of \(f\) and the \(x\)-axis. 2 marks
b. For \(x\) in the interval \((0, 1)\), show that the gradient of the tangent to the graph of \(f\) is \(\frac{1-3x}{2\sqrt{x}}\). 1 mark
The edges of the right-angled triangle \(ABC\) are the line segments \(AC\) and \(BC\), which are tangent to the graph of \(f\), and the line segment \(AB\), which is part of the horizontal axis, as shown below. Let \(\theta\) be the angle that \(AC\) makes with the positive direction of the horizontal axis, where \(45^\circ \le \theta \le 90^\circ\).
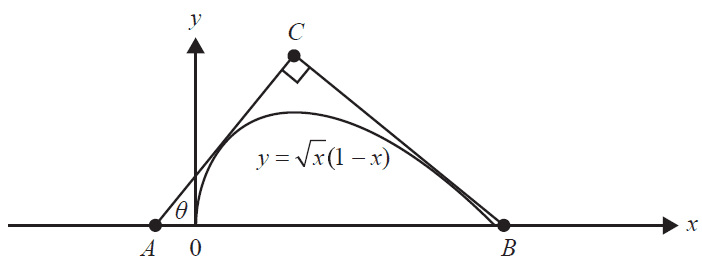
c. Find the equation of the line through \(B\) and \(C\) in the form \(y=mx+c\), for \(\theta = 45^\circ\). 2 marks
d. Find the coordinates of \(C\) when \(\theta = 45^\circ\). 4 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

