2017 VCE Maths Methods Mini Test 3
Number of marks: 10
Reading time: 2 minutes
Writing time: 15 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
A box contains five red marbles and three yellow marbles. Two marbles are drawn at random from the box without replacement.
The probability that the marbles are of different colours is
- A. \(\frac{5}{8}\)
- B. \(\frac{3}{5}\)
- C. \(\frac{15}{28}\)
- D. \(\frac{15}{56}\)
- E. \(\frac{30}{28}\)
Let \(f\) and \(g\) be functions such that \(f(2) = 5\), \(f(3) = 4\), \(g(2) = 5\), \(g(3) = 2\) and \(g(4) = 1\).
The value of \(f(g(3))\) is
- A. 1
- B. 2
- C. 3
- D. 4
- E. 5
The 95% confidence interval for the proportion of ferry tickets that are cancelled on the intended departure day is calculated from a large sample to be \((0.039, 0.121)\).
The sample proportion from which this interval was constructed is
- A. 0.080
- B. 0.041
- C. 0.100
- D. 0.062
- E. 0.059
Part of the graph of the function \(f\) is shown below. The same scale has been used on both axes.
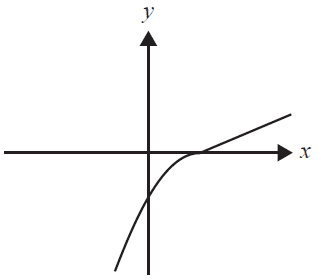
The corresponding part of the graph of the inverse function \(f^{-1}\) is best represented by
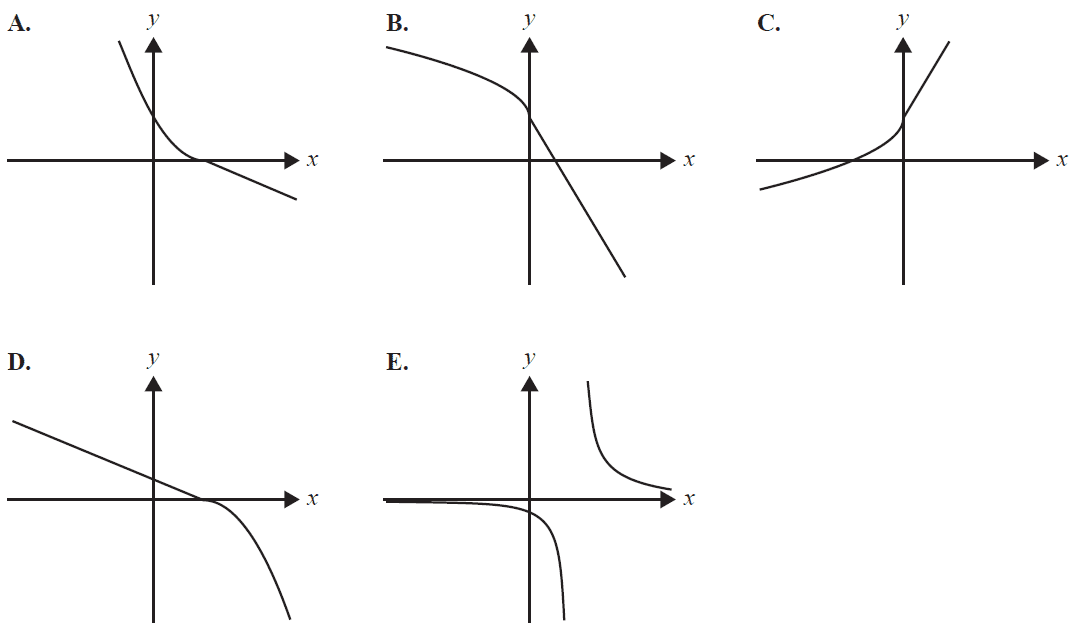
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Let \(f: [-3, 0] \to R, f(x) = (x+2)^2(x-1)\).
a. Show that \((x+2)^2(x-1) = x^3 + 3x^2 - 4\). 1 mark
b. Sketch the graph of \(f\) on the axes below. Label the axis intercepts and any stationary points with their coordinates. 3 marks
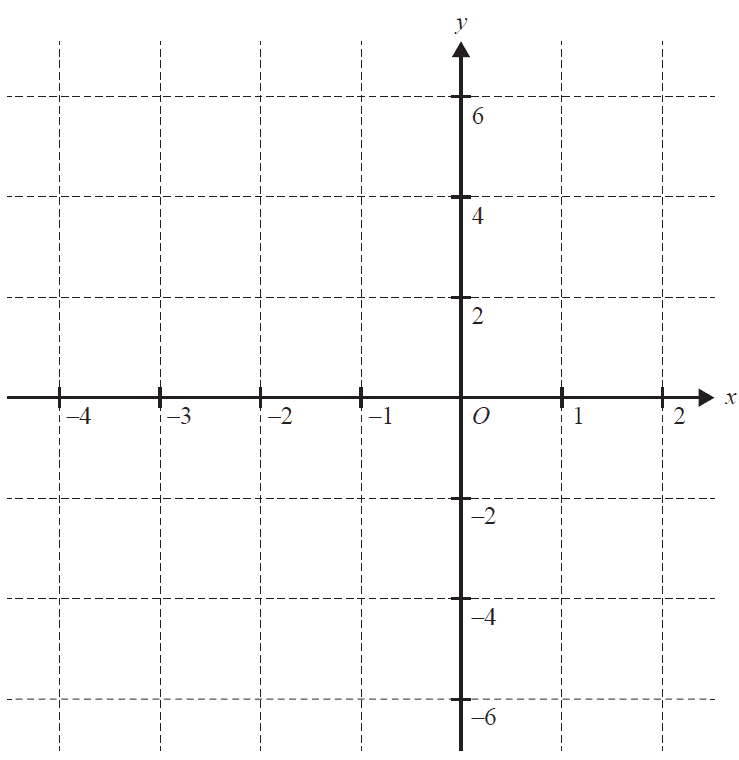
In a large population of fish, the proportion of angel fish is \(\frac{1}{4}\).
Let \(\hat{P}\) be the random variable that represents the sample proportion of angel fish for samples of size \(n\) drawn from the population.
Find the smallest integer value of \(n\) such that the standard deviation of \(\hat{P}\) is less than or equal to \(\frac{1}{100}\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

