VCE General Maths Matrices 2020 Exam 2 Mini Test

Question 1 (6 marks) [2020 Exam 2 M1 Q1]

The three major shopping centres in a large city, Eastmall (E), Grandmall (G) and Westmall (W), are owned by the same company.
The total number of shoppers at each of the centres at 1.00 pm on a typical day is shown in matrix V.
\[ V = \begin{array}{c} \begin{array}{ccc} E & G & W \end{array} \\ \begin{bmatrix} 2300 & 2700 & 2200 \end{bmatrix} \end{array} \]

a. Write down the order of matrix V. 1 mark

Each of these centres has three major shopping areas: food (F), clothing (C) and merchandise (M).
The proportion of shoppers in each of these three areas at 1.00 pm on a typical day is the same at all three centres and is given in matrix P below.

\[ P = \begin{bmatrix} 0.48 \\ 0.27 \\ 0.25 \end{bmatrix} \begin{matrix} F \\ C \\ M \end{matrix} \]

b. Grandmall’s management would like to see 700 shoppers in its merchandise area at 1.00 pm.
If this were to happen, how many shoppers, in total, would be at Grandmall at this time? 1 mark

c. The matrix \( Q = P \times V \) is shown below. Two of the elements of this matrix are missing.

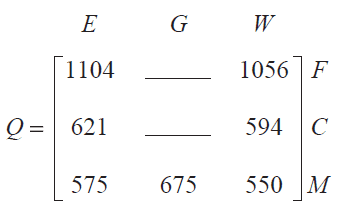
i. Complete matrix Q above by filling in the missing elements. 1 mark

ii. The element in row i and column j of matrix Q is \(q_{ij}\).
What does the element \(q_{23}\) represent? 1 mark

The average daily amount spent, in dollars, by each shopper in each of the three areas at Grandmall in 2019 is shown in matrix \(A_{2019}\) below.
\[ A_{2019} = \begin{bmatrix} 21.30 \\ 34.00 \\ 14.70 \end{bmatrix} \begin{matrix} F \\ C \\ M \end{matrix} \]

On one particular day, 135 shoppers spent the average daily amount on food, 143 shoppers spent the average daily amount on clothing and 131 shoppers spent the average daily amount on merchandise.

d. Write a matrix calculation, using matrix \(A_{2019}\), showing that the total amount spent by all these shoppers is \$9663.20. 1 mark

e. In 2020, the average daily amount spent by each shopper was expected to change by the percentage shown in the table below.

Area	food	clothing	merchandise
Expected change	increase by 5%	decrease by 15%	decrease by 1%

The average daily amount, in dollars, expected to be spent in each area in 2020 can be determined by forming the matrix product
\( A_{2020} = K \times A_{2019} \)
Write down matrix \(K\). 1 mark

\( K = \)

Question 2 (3 marks) [2020 Exam 2 M1 Q2]

The preferred number of cafes (x) and sandwich bars (y) in Grandmall’s food court can be determined by solving the following equations written in matrix form.
\[ \begin{bmatrix} 5 & -9 \\ 4 & -7 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 7 \\ 6 \end{bmatrix} \]

a. The value of the determinant of the \( 2 \times 2 \) matrix is 1.
Use this information to explain why this matrix has an inverse. 1 mark

b. Write the three missing values of the inverse matrix that can be used to solve these equations. 1 mark

c. Determine the preferred number of sandwich bars for Grandmall’s food court. 1 mark

Question 3 (4 marks) [2020 Exam 2 M1 Q3]

An offer to buy the Westmall shopping centre was made by a competitor.
One market research project suggested that if the Westmall shopping centre were sold, each of the three centres (Westmall, Grandmall and Eastmall) would continue to have regular shoppers but would attract and lose shoppers on a weekly basis.
Let \(S_n\) be the state matrix that shows the expected number of shoppers at each of the three centres \(n\) weeks after Westmall is sold.
A matrix recurrence relation that generates values of \(S_n\) is

\(S_{n+1} = T \times S_n\)

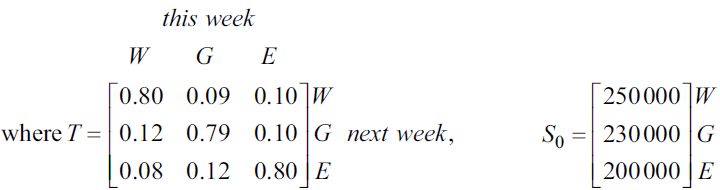
a. Calculate the state matrix, \(S_1\), to show the expected number of shoppers at each of the three centres one week after Westmall is sold. 1 mark

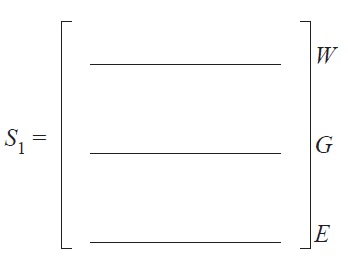
Using values from the recurrence relation on page 23, the graph below shows the expected number of shoppers at Westmall, Grandmall and Eastmall for each of the 10 weeks after Westmall is sold.

b. What is the difference in the expected weekly number of shoppers at Westmall from the time Westmall is sold to 10 weeks after Westmall is sold?
Give your answer correct to the nearest thousand. 1 mark

c. Grandmall is expected to achieve its maximum number of shoppers sometime between the fourth and the tenth week after Westmall is sold.
Write down the week number in which this is expected to occur. 1 mark

d. In the long term, what is the expected weekly number of shoppers at Westmall?
Round your answer to the nearest whole number. 1 mark

Question 4 (2 marks) [2020 Exam 2 M1 Q4]

A second market research project also suggested that if the Westmall shopping centre were sold, each of the three centres (Westmall, Grandmall and Eastmall) would continue to have regular shoppers but would attract and lose shoppers on a weekly basis.
Let \(R_n\) be the state matrix that shows the expected number of shoppers at each of the three centres \(n\) weeks after Westmall is sold.
A matrix recurrence relation that generates values of \(R_n\) is

\( R_{n+1} = TR_n + B \)

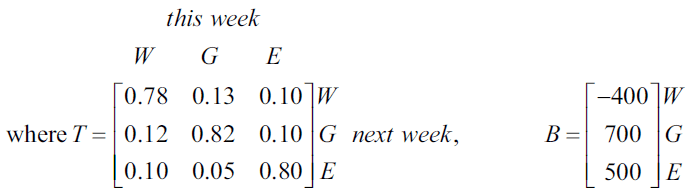
The matrix \(R_2\) is the state matrix that shows the expected number of shoppers at each of the three centres in the second week after Westmall is sold.

\[ R_2 = \begin{bmatrix} 239\,060 \\ 250\,840 \\ 192\,900 \end{bmatrix} \begin{matrix} W \\ G \\ E \end{matrix} \]

a. Determine the expected number of shoppers at Westmall in the third week after it is sold. 1 mark

b. Determine the expected number of shoppers at Westmall in the first week after it is sold. 1 mark