QCAA Maths Methods Paper 2 Integral Calculus Mini Test 3
External Assessment Paper 2 — Technology-active
Number of marks: 11
Perusal time: 1 minute
Writing time: 15 minutes
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A particle is moving in a straight line. The velocity (m s\(^{-1}\)) of the particle is given by \[v(t) = \frac{20\sin(2t)}{6-5\cos(2t)}, t \ge 0,\] where \(t\) is time (s) after moving from its initial position.
The initial position of the particle is +6.0 m from the origin.
a) Use calculus methods to determine an equation for the position of the particle from the origin at any time \(t\). [3 marks]
b) Determine the position of the particle relative to the origin when it first reaches maximum velocity. [3 marks]
A company makes windows using glass that has a mass of 5.6 kg per square metre. A customer orders an unusual window in a partial parabolic shape, as shown.
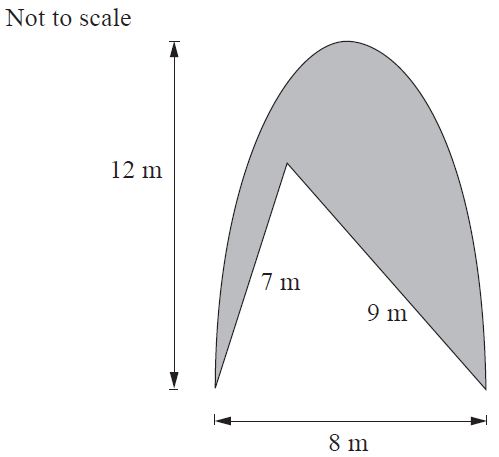
Determine the mass of the window.
END OF PAPER



