QCAA Maths Methods Paper 2 Integral Calculus Mini Test 2
External Assessment Paper 2 — Technology-active
Number of marks: 10
Perusal time: 1 minute
Writing time: 15 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
Using the trapezoidal rule with an interval size of 1, the approximate value of the integral \(\int_0^3 0.5^x dx\) is
- (A) 1.25
- (B) 1.26
- (C) 1.31
- (D) 1.88
Oil is leaking from a tanker at the rate of \(r(t) = 9000e^{-0.2t}\) litres per hour, where \(t\) is in hours.
Determine how much oil leaks from the tanker (to the nearest litre) from time \(t = 0\) to time \(t = 10\).
- (A) 38 910 litres
- (B) 8756 litres
- (C) 7782 litres
- (D) 1556 litres
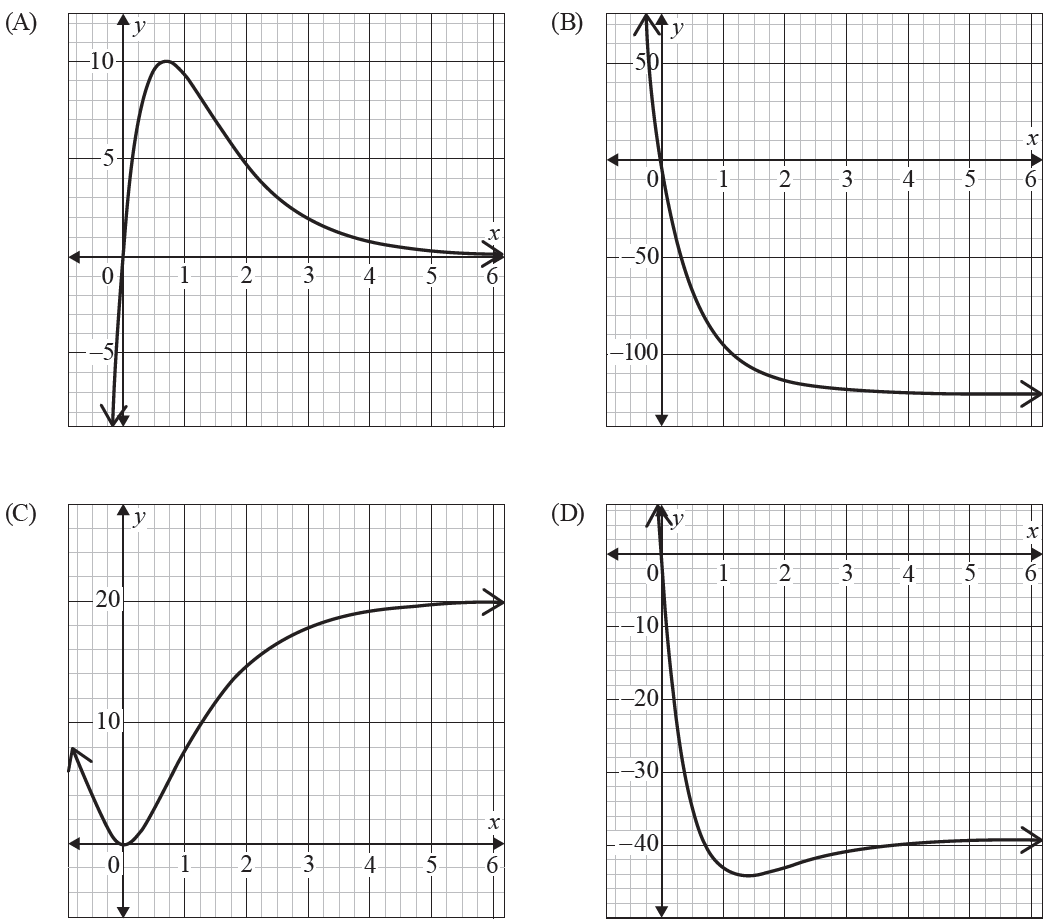
An object moves in a straight line with a velocity \(v\) given by
\[ v(t) = 40(e^{-t} - e^{-2t}) \text{ m s}^{-1} \text{ where } t \ge 0 \]The object is at the origin initially. The displacement-time graph in the first 6 seconds is
Let \(R\) be the region enclosed by the graph of \(y = xe^x\), the x-axis, and the lines \(x = -1\) and \(x = 1\).
The area of \(R\) is closest to
- (A) 0.74
- (B) 1.26
- (C) 2.35
- (D) 3.09
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
Over a suitable domain, a hill has a cross-sectional area given by \(\int h(x)dx = \frac{a}{b}e^{bx} + c\), where:
- • \(a\), \(b\) and \(c\) are constants, \(b \ne 0\)
- • \(h(x)\) represents vertical distance (m), \(x\) represents horizontal distance (m).
It is known that \(h(0) = 1.22\) and \(h(40) = 25\).
Where the gradient of the hill is 0.86 there is a tree stump. A second tree stump is located further up the hill. The difference in hill gradient between the two tree stumps is 0.44.
A surveyor predicts that the vertical distance separating the two tree stumps is between 7.5 m and 8.5 m. Evaluate the reasonableness of this prediction.
END OF PAPER


