2023 QCAA Maths Methods External Exam Paper 2
Paper 2 — Technology-active
This is the full QCE Maths Methods External Exam with worked solutions. You can also try Mini-Tests, which are official QCAA exams split into short tests you can do anytime.
Number of marks: 55
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
If \(f(x) = \sin(3x)\), determine the value of \(f'(\frac{\pi}{8})\).
- (A) 2.772
- (B) 1.148
- (C) 0.929
- (D) 0.383
The probability of hitting a bullseye on a standard dartboard is 1 in 1250. What is the probability of hitting a bullseye exactly once in 10 attempts?
- (A) \(\binom{9}{1} \times (\frac{1}{1250})^1 \times (\frac{1249}{1250})^9\)
- (B) \(\binom{9}{1} \times (\frac{1}{1250})^0 \times (\frac{1249}{1250})^1\)
- (C) \(\binom{10}{1} \times (\frac{1}{1250})^1 \times (\frac{1249}{1250})^9\)
- (D) \(\binom{10}{1} \times (\frac{1}{1250})^9 \times (\frac{1249}{1250})^1\)
In a certain normal distribution curve, 95% of the area lies between the values 50.32 and 113.68. The mean of this distribution is 82.
Determine the standard deviation.
- (A) 16.16
- (B) 21.12
- (C) 31.68
- (D) 63.36
The displacement (m) of a moving particle is given by \(d = e^{0.5t} - 1\), where \(t\) is time (s). The acceleration (m s\(^{-2}\)) of the particle when \(t = 4\) is
- (A) 7.3891
- (B) 6.3891
- (C) 3.6945
- (D) 1.8473
Solve \(\ln(x) + \ln(3.70) = \ln(9.25)\) for \(x\).
- (A) 0.92
- (B) 1.71
- (C) 2.50
- (D) 5.55
\(\int_{a}^{5a} \frac{1}{x+a} dx\), \(a \neq 0\) is
- (A) 1.7918
- (B) 1.6094
- (C) 1.3863
- (D) 1.0986
The distribution of a certain sample proportion has a mean of 0.70 and a standard deviation of 0.02.
Determine the sample size.
- (A) 525
- (B) 750
- (C) 1750
- (D) 2500
The number of koalas in a conservation park is modelled by \(N = 15 \ln(7t + 1)\), \(t \ge 1\), where \(t\) represents the time (years) since the park opened. There were 20 koalas in the park when it opened.
Determine the approximate rate of change in the number of koalas when \(t = 3\).
- (A) 46
- (B) 26
- (C) 25
- (D) 5
If \(f(x) = e^{3x}(x+1)^2\) and \(f'(x) = ae^{3x}(x+1)\), determine the expression for \(a\).
- (A) 3x + 5
- (B) 3x + 3
- (C) 5x + 5
- (D) 5x + 3
A student is trying to determine which subject they performed best in compared to other students. Results from recent tests in four subjects (A to D) are shown. Assume student results in each subject are normally distributed.
In which subject did the student perform best compared to other students?
| Class mean | Class standard deviation |
Student's result |
|
|---|---|---|---|
| (A) | 62 | 22 | 77 |
| (B) | 55 | 25 | 74 |
| (C) | 61 | 15 | 70 |
| (D) | 73 | 20 | 82 |
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A researcher found that 17 out of 50 randomly selected people had used public transport in the past week.
a) Determine the sample proportion of people who had used public transport in the past week. [1 mark]
b) Determine an approximate 95% confidence interval for the proportion of people who had used public transport in the past week. [2 marks]
c) Someone claims that: 50% of people use public transport each week.
Use your answer from Question 11b) to explain whether the data can or cannot support this claim. [1 mark]
The graph shows the water level under a bridge over a 12-hour period.
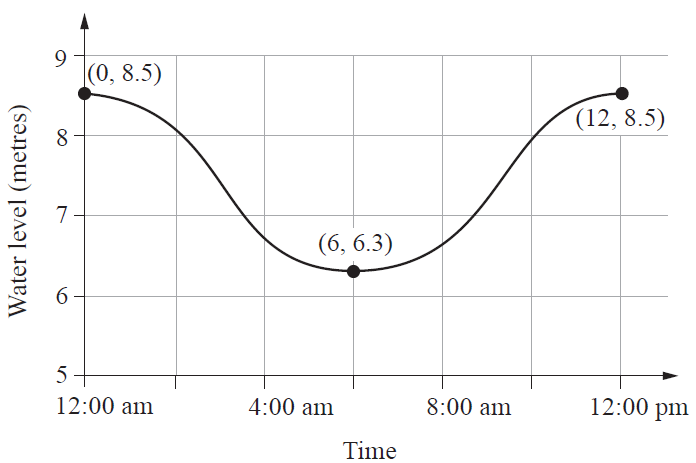
a) Determine the equation of the cosine function that models the water level as a function of time after 12:00 am. [1 mark]
b) How long in the 12-hour period shown is the rate of change of water level more than 0.55 metres per hour? [3 marks]
The curved lines represent graphs of the equations \(y = x^2 - 4x + 8\) and \(y = 10\cos(x+10)\).
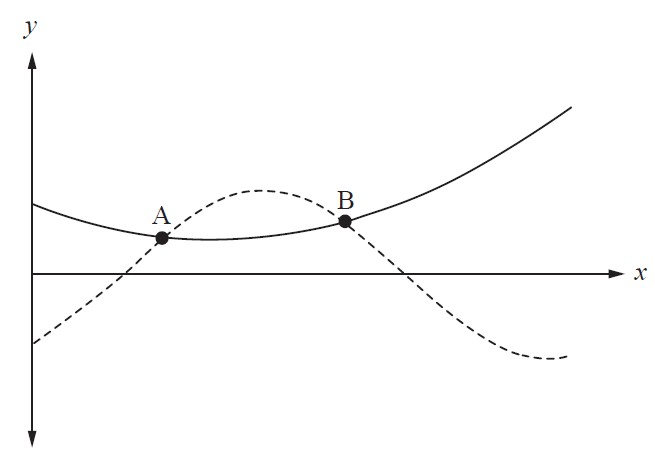
a) Determine the coordinates of the points of intersection A and B. [1 mark]
b) State an integral expression representing the area enclosed by the two graphs. [2 marks]
c) Determine the area enclosed by the two graphs. [1 mark]
A fence divides a paddock into two triangular sections as shown.
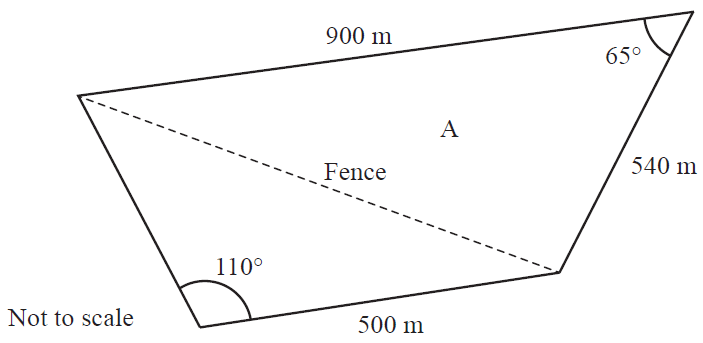
a) Determine the length of the fence. [1 mark]
b) Calculate the area of triangular section A. [1 mark]
c) Determine the total area of the paddock. [5 marks]
Determine the derivative of \(f(x) = \ln x^2 + \ln(x-5)^3\). Express the derivative as a single fraction in its simplest and factorised form.
A particle is moving in a straight line. The velocity (m s\(^{-1}\)) of the particle is given by \[v(t) = \frac{20\sin(2t)}{6-5\cos(2t)}, t \ge 0,\] where \(t\) is time (s) after moving from its initial position.
The initial position of the particle is +6.0 m from the origin.
a) Use calculus methods to determine an equation for the position of the particle from the origin at any time \(t\). [3 marks]
b) Determine the position of the particle relative to the origin when it first reaches maximum velocity. [3 marks]
Model bridges were constructed for a competition. The models that could support the heaviest loads before collapsing were given awards.
The load results of the competition were normally distributed, with a mean of 1.36 kg and a standard deviation of 0.12 kg.
Three award categories were used: honours for the top 15% of load results; distinction for the next 15%; and commendation for the next 15%.
The model bridge constructed by Finley only just missed out on a commendation. Kirby's model bridge only just qualified for honours. Determine the difference, to the nearest gram, between the loads supported by Finley and Kirby's models.
A company makes windows using glass that has a mass of 5.6 kg per square metre. A customer orders an unusual window in a partial parabolic shape, as shown.
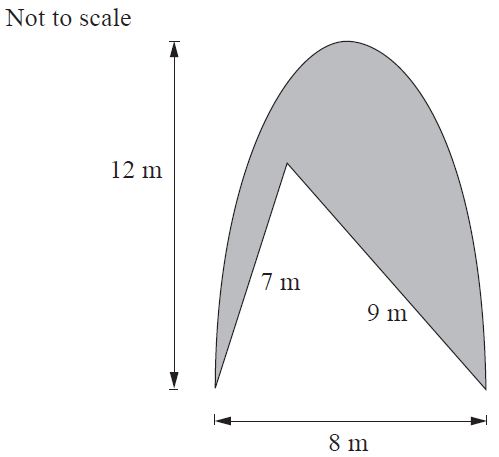
Determine the mass of the window.
Over a suitable domain, a hill has a cross-sectional area given by \(\int h(x)dx = \frac{a}{b}e^{bx} + c\), where:
- • \(a\), \(b\) and \(c\) are constants, \(b \ne 0\)
- • \(h(x)\) represents vertical distance (m), \(x\) represents horizontal distance (m).
It is known that \(h(0) = 1.22\) and \(h(40) = 25\).
Where the gradient of the hill is 0.86 there is a tree stump. A second tree stump is located further up the hill. The difference in hill gradient between the two tree stumps is 0.44.
A surveyor predicts that the vertical distance separating the two tree stumps is between 7.5 m and 8.5 m. Evaluate the reasonableness of this prediction.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/


