WACE Maths Methods ATAR Section 2 Topic Tests
Continuous Random Variables Topic Test 1
Section Two: Technology-active
Number of marks: 13
Reading time: 1 minute
Writing time: 13 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Mrs Euler is having her car serviced at BIMDAS Mechanics. She drops her vehicle off at 8 am and is told that her car will be ready for collection at some time between 1 pm and 5 pm that day.
Let the random variable \(B\) denote the time after noon (12 pm) at which a vehicle is ready for collection at BIMDAS Mechanics. The probability density function for \(B\) is shown in the graph below.
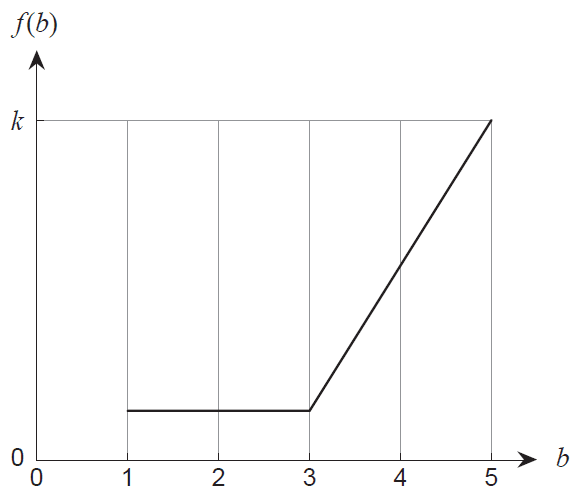
The probability of a vehicle being ready for collection between 2 pm and 3 pm is 0.1.
(a) Determine the value of \(k\). (2 marks)
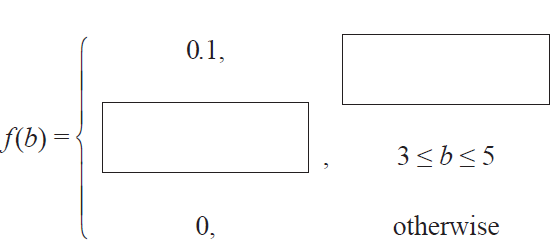
(b) An incomplete expression for the probability density function of \(B\) is given below. Fill in the boxes to complete the missing parts of the expression. (2 marks)
(c) Determine the expected time that Mrs Euler's vehicle will be ready for collection at BIMDAS Mechanics. (3 marks)
Mr Euler is also having his car serviced, but by Addition Autos. He drops his vehicle off at 8 am and is told that his car will be ready for collection at some time between 1 pm and 5 pm that day.
Let the random variable \(A\) denote the time after noon (12 pm) that a vehicle is ready for collection at Addition Autos. The cumulative distribution function for \(A\) is given by \[ P(A \le a) = \begin{cases} 0, & a < 1 \\ \frac{10a - a^2 - 9}{16}, & 1 \le a \le 5 \\ 1, & a > 5 \end{cases} \]
(d) Determine the probability that Mr Euler's vehicle will be ready to collect
(i) by 3 pm. (1 mark)
(ii) between 3 pm and 4 pm. (2 marks)
(e) Determine the expected time at which Mr Euler's vehicle will be ready for collection at Addition Autos. (3 marks)
End of questions
Continuous Random Variables Topic Test 2
Section Two: Technology-active
Number of marks: 9
Reading time: 1 minute
Writing time: 9 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A pizza shop estimates that the time \(X\) hours to deliver a pizza from when it is ordered is a continuous random variable with probability density function given by
\[ f(x) = \begin{cases} \frac{4}{3} - \frac{2}{3}x, & 0 < x < 1 \\ 0, & \text{otherwise.} \end{cases} \]
(a) What is the probability of a pizza being delivered within half an hour of being ordered? (2 marks)
(b) Calculate the mean delivery time to the nearest minute. (3 marks)
(c) Calculate the standard deviation of the delivery time to the nearest minute. (4 marks)
End of questions
Continuous Random Variables Topic Test 3
Section Two: Technology-active
Number of marks: 10
Reading time: 1 minute
Writing time: 10 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
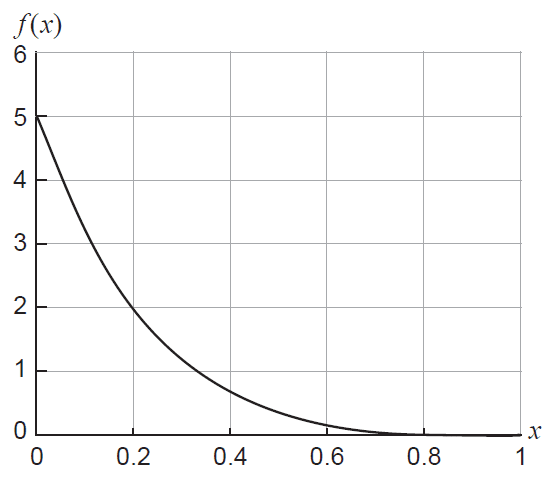
A small outback petrol station receives a weekly delivery of petrol. The volume of petrol sold in a week, \(X\), (in units of 10 000 litres) is a random variable with probability density function
\[ f(x) = 5(1-x)^4, \quad 0 \le x \le 1 \]
as shown in the graph below.
(a) Determine, using appropriate units, the expected value and variance of the amount of fuel sold in a week. (4 marks)
(b) What storage tank capacity will ensure that there is only a 1% chance of running out of petrol in a given week? State your answer to the nearest litre. (3 marks)
(c) When the petrol is delivered, it is pumped into the storage tank. The rate of change of the petrol level in the tank, \(h(t)\), (measured in metres) at time \(t\) (measured in minutes) is given by
\[ h'(t) = \frac{5}{2t+3} \]
Determine the height of the storage tank if it takes 20 minutes to fill. (3 marks)
End of questions
Continuous Random Variables Topic Test 4
Section Two: Technology-active
Number of marks: 10
Reading time: 1 minute
Writing time: 10 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The following function is a probability density function on the given interval:
\[ f(x) = \begin{cases} ax^2(x-2) & \text{for } 0 \le x \le 2 \\ 0 & \text{otherwise} \end{cases} \]
(a) Find the value of \(a\). (3 marks)
(b) Find the probability that \(x \ge 1.2\). (2 marks)
(c) Find the median of the distribution. (2 marks)
End of questions


