WACE Maths Methods ATAR Section 2 Topic Tests

Question 1 (14 marks) [2022 Section 2 Q9]

Andrew plans to run a game called Lucky Cup for a school fundraising event. All profits go toward the school's fundraising efforts. The game consists of three standard dice, each placed into a red cup. The red cup is shaken, the dice rolled, and the number of sixes recorded.

Let \(X\) be a random variable denoting the number of sixes rolled in a game of Lucky Cup.

(a) State the distribution of \(X\). (2 marks)

An incomplete probability distribution for \(X\) is shown in the table below.

\(x\)	0	1	2	3
\(P(X=x)\)	\(\frac{125}{216} \approx 0.5787\)

(b) Complete the table above, providing the missing probabilities. (2 marks)

Lucky Cup costs $1 to play. If a player rolls one 6 they win $1, if they roll two 6s they win $2, and if they roll three 6s they win $3.

(c) Determine the school's expected profit/loss for each game of Lucky Cup. (3 marks)

(d) Determine the probability that a player will make a profit in a game of Lucky Cup. (2 marks)

Andrew wants to increase the attraction of the game by providing the opportunity for larger winnings. He modifies the rules of the game so that players only win money when two or more 6s are rolled, and the winnings for rolling three 6s is three times as much as the winnings for rolling two 6s. Each game still costs $1 to play. He estimates that he should be able to run 500 games and wants to make a profit of $200 for the school.

Andrew calls this game Lucky Cup II.

(e) Determine the winnings Andrew should set for rolling three 6s in Lucky Cup II. (3 marks)

Andrew decides to make the game even more dynamic and exciting. He adds a green cup with a die that he rolls at the beginning of each game. The value that Andrew rolls becomes the target value, and players must roll this target value to win. For example, if Andrew rolls a 2 from the green cup and a player rolls three 2s, the player wins the top prize.

Andrew calls this game Lucky Cup III.

(f) Explain how this change affects a player's chance of winning compared with Lucky Cup II. (2 marks)

Question 1 (8 marks) [2020 Section 2 Q9]

A cake shop makes birthday cakes. The probability distribution of the number of birthday cakes sold in a day, \(X\), is given below.

\(x\)	0	1	2	3	4
\(P(X=x)\)	0.1	0.2	0.25	0.35	0.1

(a) Calculate the mean number or birthday cakes sold in a day. (1 mark)

(b) On Monday, the cake shop makes four birthday cakes. If each birthday cake costs $20 to make and sells for $50, what is the expected profit or loss on that day? (3 marks)

On Tuesday, the shop makes three birthday cakes. Let the random variable \(Y\) denote the number of birthday cakes not sold on that day.

(c) Explain why \(P(Y=0) = 0.45\). (2 marks)

(d) Obtain the probability distribution of \(Y\). (2 marks)

Question 1 (9 marks) [2017 Section 2 Q13]

Ravi runs a dice game in which a player throws two standard six-sided dice and the sum of the uppermost faces is calculated. If the sum is less than five, the player wins $20. If the sum is greater than eight, the player wins $10. Otherwise the player receives no money.

(a) Complete the table below. (2 marks)

Amount won
Probability

(b) What is the expected amount of money won by a player each time they play? (2 marks)

(c) Liu Yang decides to play the game. If Ravi charges her $5 to roll two dice, who is likely to be better off in the long-term? Explain. (3 marks)

(d) If Ravi wants to make a long-term profit per game of 20% of what he charges, what should he charge a player to roll the two dice? (2 marks)

Question 1 (14 marks) [2024 Section 2 Q14]

A mathematics teacher, Mr Ulam, devises a new game that uses four standard dice. A player rolls all the dice. Any dice with a 1 facing up are winning dice and are removed. The remaining dice are rolled again. The game is finished when a player has two or more winning dice.

Mr Ulam plays the game 500 times and records how many rolls it takes to win. Let \(X\) be a random variable denoting the number of rolls needed to win a game. The frequency results, \(f\), are displayed in the graph below.

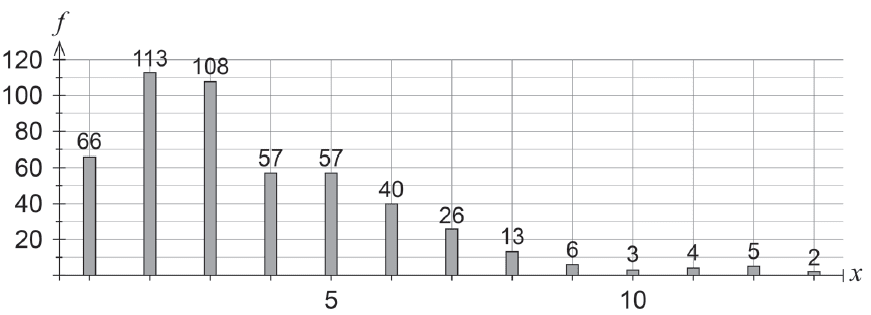
(a) Using the experimental data above, estimate the probability of

(i) winning in exactly two rolls. (1 mark)

(ii) not winning in two or less rolls. (2 marks)

(b) State two reasons why the game cannot be modelled using a binomial distribution. (2 marks)

Mr Ulam uses a computer to simulate 10 000 games to better estimate the probability of each outcome. The results of the simulations are summarised in the table below.

\(x\)	1	2	3	4	5	6	7	8
\(P(X=x)\)	0.134	0.215	0.208	0.153	0.106	0.067	0.047	0.030
\(x\)	9	10	11	12	13	14	15	16
\(P(X=x)\)	0.016	0.012	0.005	0.003	0.002	0.001	0.001	0.000

To fundraise for a local charity, Mr Ulam charges $1 for each game, and pays out winnings as follows:

• if the game is won in one or two rolls the player wins $2
• if the game is won in three rolls the player wins $1 (i.e. their money back)
• if the game is won in four or more rolls the player wins nothing.

Let \(Y\) be a random variable denoting the profit for a player who plays a $1 game.

(c) Using the data above, complete the probability distribution table for \(Y\). (3 marks)

\(y\)
\(P(Y=y)\)

(d) Calculate the

(i) expected value of \(Y\). (2 marks)

(ii) variance of \(Y\). (2 marks)

(e) In the long run, do you expect that the game will be profitable for the charity? Justify your answer. (2 marks)