WACE Maths Methods ATAR Section 2 Topic Tests
Integral Calculus Topic Test 1
Section Two: Technology-active
Number of marks: 12
Reading time: 1 minute
Writing time: 12 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
An oscillating mass has a velocity, \(v\), given by \[ v(t) = 2t \cos\left(t + \frac{\pi}{2}\right) \quad \text{for } t \ge 0. \] The velocity is given in metres per second, and the time, \(t\), is given in seconds. A graph of the velocity of the mass' motion is shown below.
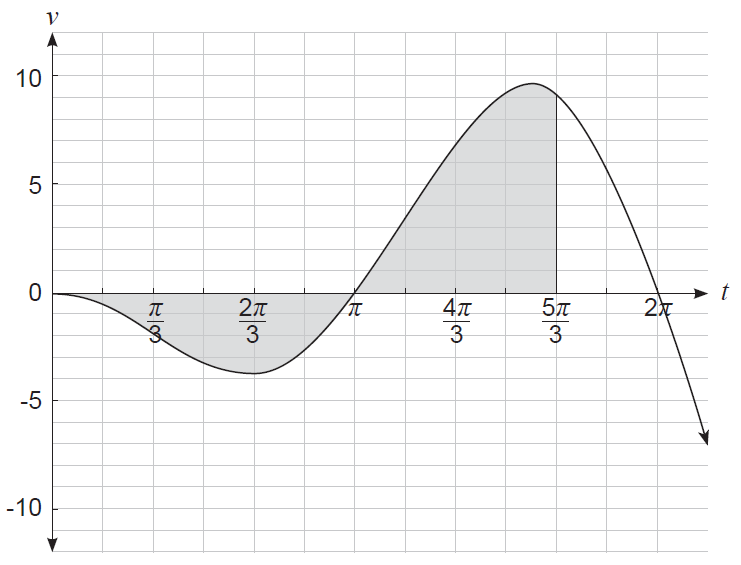
(a) Determine the first two times, \(t > 0\), at which the mass changes direction. State your answers exactly. (2 marks)
(b) What does the signed area of the shaded region in the figure represent? (2 marks)
(c) Write an integral expression for the distance travelled from \(t = \frac{\pi}{3}\) to \(t = \frac{4\pi}{3}\). (3 marks)
(d) Determine the first time after \(t = \pi\) that the acceleration of the object will be 0 m/s\(^2\). (2 marks)
(e) The displacement of the mass is given by \[ x(t) = A \sin\left(t + \frac{\pi}{2}\right) + B \cos\left(t + \frac{\pi}{2}\right) + 2t \sin\left(t + \frac{\pi}{2}\right) \] where \(A\) and \(B\) are constants. Determine the value of \(A\) and \(B\). (3 marks)
End of questions
Integral Calculus Topic Test 2
Section Two: Technology-active
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The 100 m sprint is a race run on a straight section of track. During a race the velocity, \(v\), measured in metres per second, of an athlete is given by
\[ v(t) = -10e^{-0.8t} - 0.05e^{0.2t} + 10.05 \]where \(t\) is the time, in seconds, measured from the moment the athlete starts to move from the start line.
(a) Determine the acceleration of the athlete three seconds after moving from the start line. (2 marks)
(b) Using calculus, determine the maximum velocity of the athlete during the race, and the time, \(t\), at which it is achieved. (4 marks)
(c) The displacement, \(x\), of the athlete is 0 m at the start of the race. Determine an expression for the displacement of the athlete during the race. (3 marks)
(d) Determine the time, \(t\), at which the athlete finishes the 100 m race. (2 marks)
End of questions
Integral Calculus Topic Test 3
Section Two: Technology-active
Number of marks: 16
Reading time: 1 minute
Writing time: 16 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The displacement, \(x\), of a mass on the end of a damped spring is given by
\[ x(t) = 3e^{-t} \sin(t), \quad t \ge 0 \]where \(x\) is in centimetres and \(t\) is in seconds.
(a) Determine when the mass first returns to its starting position at \(x = 0\). (2 marks)
(b) Determine an expression for the velocity of the mass. (2 marks)
(c) Determine the displacement of the mass when it first changes direction. (3 marks)
(d) The mass is considered to have stopped oscillating when the oscillation amplitude \(A(t) = 3e^{-t}\) drops to 0.01 cm. How long does it take for the spring to stop oscillating? (2 marks)
The graph of the cubic function \( f(x) = ax^3 + bx^2 + cx + d \) is shown below. A turning point is located at (1, 0) and the shaded region shown on the graph has an area of \( \frac{3}{2} \) units².
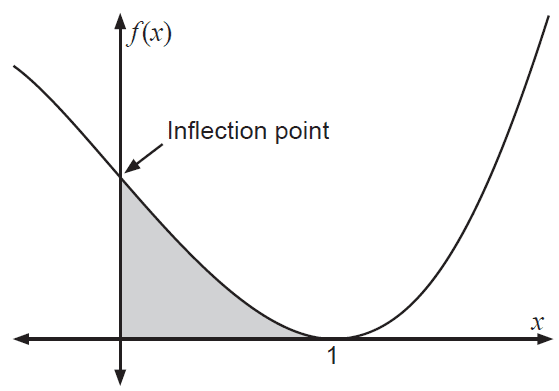
Use the above information to determine the values of \(a\), \(b\), \(c\) and \(d\).
End of questions
Integral Calculus Topic Test 4
Section Two: Technology-active
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The displacement in metres, \(x(t)\), of a power boat \(t\) seconds after it was launched is given by:
\[ x(t) = \frac{5t(t^2 - 15t + 48)}{6}, \quad t \ge 0 \]How far has the power boat travelled before its acceleration is zero?
A team of oceanographers surveyed the depth of the ocean in a region populated by a particular endangered fish species. They discovered a large trench extending below the otherwise flat seabed as shown in the figure below.
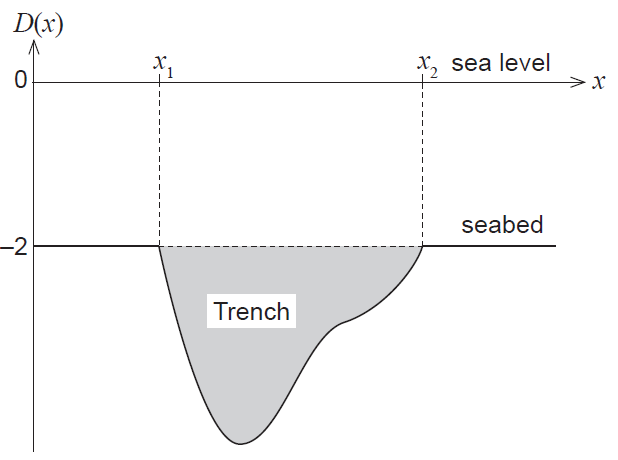
The displacement, in kilometres, from sea level to the ocean floor is given by
\[ D(x) = \begin{cases} (x - 4)^2 + \cos(2x - 3\pi) - 5, & x_1 \le x \le x_2 \\ -2, & \text{otherwise} \end{cases} \]where \(x\) (measured in kilometres) is the east-west horizontal displacement relative to a reference marker at sea level.
(a) With reference to the figure above:
(i) determine the values of \(x_1\) and \(x_2\). (2 marks)
(ii) use calculus to determine the cross-sectional area of the trench shaded in the figure above. (3 marks)
(b) Using calculus, determine the maximum distance of the trench below sea level. (5 marks)
End of questions
Integral Calculus Topic Test 5
Section Two: Technology-active
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
David and Katrina have a small farm and wish to fence off an area of their land so they can raise sheep. The area they have chosen has one border along a road as shown in the diagram below.
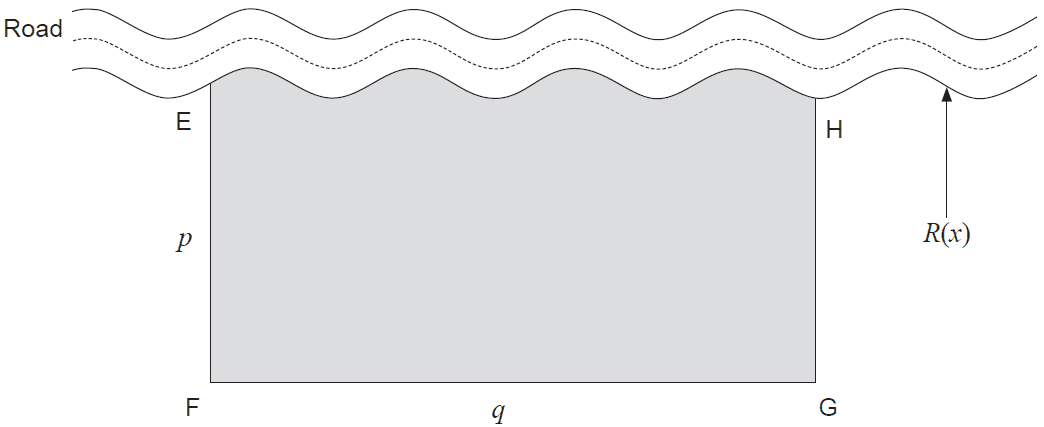
The enclosure is shown as the shaded area above and has right angles at points F and G. David and Katrina want the combined lengths of the fencing from E to F and F to G to equal 500 metres. Let the length of fence EF be equal to \(p\) metres and the length of fence FG be equal to \(q\) metres. If we locate the origin at point F and the x-axis along the line FG, the equation defining the fence along the road is given by:
\[ R(x) = 10 \sin\left(\frac{x}{15}\right) + p \](a) Show that the equation defining the area of the enclosure, \(A(q)\), can be given in terms of \(q\) as follows:
\[ A(q) = 500q - 150 \cos\left(\frac{q}{15}\right) - q^2 + 150 \] (4 marks)(b) Determine, to the nearest metre, the value of \(q\) that will allow the sheep to graze over the maximum area and state this maximum area. (4 marks)
The length of the fence from E to H is given by the equation:
\[ L_{EH} = \int_0^q \sqrt{1 + (R'(x))^2} \, dx \text{, where } R'(x) \text{ is the first derivative of } R(x). \](c)
(i) Determine \(R'(x)\). (1 mark)
(ii) Hence determine the total length of fencing required by David and Katrina to enclose their sheep with maximum area for grazing. (3 marks)
End of questions
Integral Calculus Topic Test 6
Section Two: Technology-active
Number of marks: 9
Reading time: 1 minute
Writing time: 9 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The line \(y=x+c\) is tangent to the graph of \(f(x)=e^x\).
(a) Obtain the coordinates of the point of intersection of the tangent with the graph of \(f(x)\). (2 marks)
(b) What is the value of \(c\)? (1 mark)
(c) Sketch the graph of \(f(x)\) and the tangent on the axes below. (1 mark)
(d) Evaluate the exact area between the graph of \(f(x)\), the tangent line, and the line \(x=\ln 2\). (3 marks)
(e) Given that \(g(x)\) is the inverse function of \(f(x)\), write a definite integral that could be used to determine the area between the graph of \(g(x)\), the x-axis, and the line \(x=\ln 2\). (2 marks)
End of questions
Integral Calculus Topic Test 7
Section Two: Technology-active
Number of marks: 17
Reading time: 1 minute
Writing time: 17 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A partially filled shampoo bottle has a uniform parabolic cross-section as shown in the diagram below.
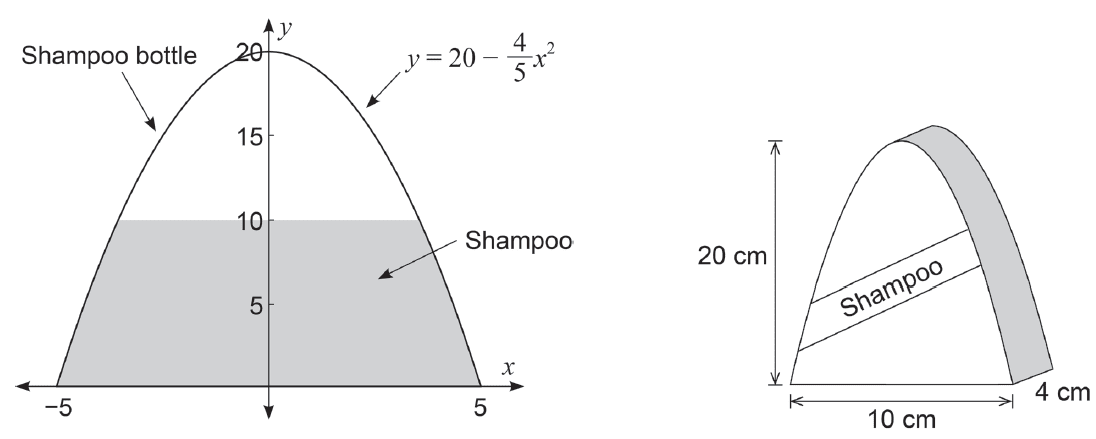
Both \(x\) and \(y\) are measured in centimetres. The width of the bottle perpendicular to the parabolic cross-section is 4 cm.
(a) Calculate the volume \(V\) of shampoo in the bottle, if it is partially filled to a height of 10 cm. (4 marks)
The bottle is turned upside down and the entire volume of the shampoo allowed to settle, as shown in the diagram below.
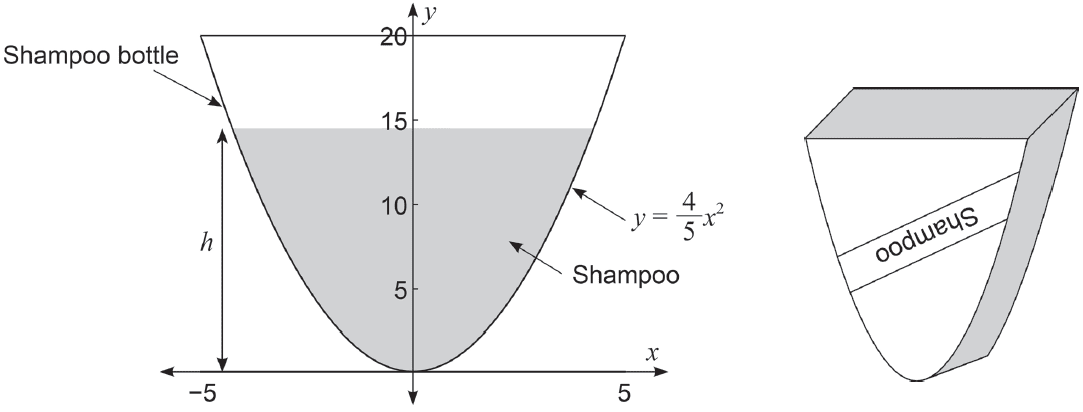
(b) Determine the shampoo level \(h\). (4 marks)
The line \(y=x+c\) is tangent to the graph of \(f(x)=e^x\).
(a) Obtain the coordinates of the point of intersection of the tangent with the graph of \(f(x)\). (2 marks)
(b) What is the value of \(c\)? (1 mark)
(c) Sketch the graph of \(f(x)\) and the tangent on the axes below. (1 mark)

(d) Evaluate the exact area between the graph of \(f(x)\), the tangent line, and the line \(x=\ln 2\). (3 marks)
(e) Given that \(g(x)\) is the inverse function of \(f(x)\), write a definite integral that could be used to determine the area between the graph of \(g(x)\), the x-axis, and the line \(x=\ln 2\). (2 marks)
End of questions
Integral Calculus Topic Test 8
Section Two: Technology-active
Number of marks: 14
Reading time: 1 minute
Writing time: 14 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A model train travels on a straight track such that its acceleration after \(t\) seconds is given by \(a(t) = pt - 13\) cm/s², \(0 \le t \le 10\), where \(p\) is a constant.
(a) Determine the initial acceleration of the model train. (1 mark)
The model train has an initial velocity of 5 cm/s. After 2 seconds it has a displacement of -50 cm. A further 4 seconds later its displacement is 178 cm.
(b) Determine the value of the constant \(p\). (4 marks)
(c) When is the model train at rest? (2 marks)
(d) How far has the model train travelled when its acceleration is 47 cm/s²? (2 marks)
(a) The table below examines the values of \( \frac{a^h-1}{h} \) for various values of \(a\) as \(h\) approaches zero. Complete the table, rounding your values to five decimal places. (2 marks)
| \(h\) | \(a=2.60\) | \(a=2.70\) | \(a=2.72\) | \(a=2.80\) |
|---|---|---|---|---|
| 0.1 | 1.00265 | 1.05241 | 1.08449 | |
| 0.001 | 0.95597 | 0.99375 | ||
| 0.00001 | 0.95552 | 1.02962 |
It can be shown that \(\frac{d}{dx}(a^x) = a^x \lim_{h \to 0}\left(\frac{a^h-1}{h}\right)\).
(b) What is the exact value of \(a\) for which \(\frac{d}{dx}(a^x) = a^x\)? Explain how the above definition and the table in part (a) support your answer. (3 marks)
End of questions
Integral Calculus Topic Test 9
Section Two: Technology-active
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A new entertainment venue is being proposed. The preliminary design has a constant cross-section, as shown in the figure below.
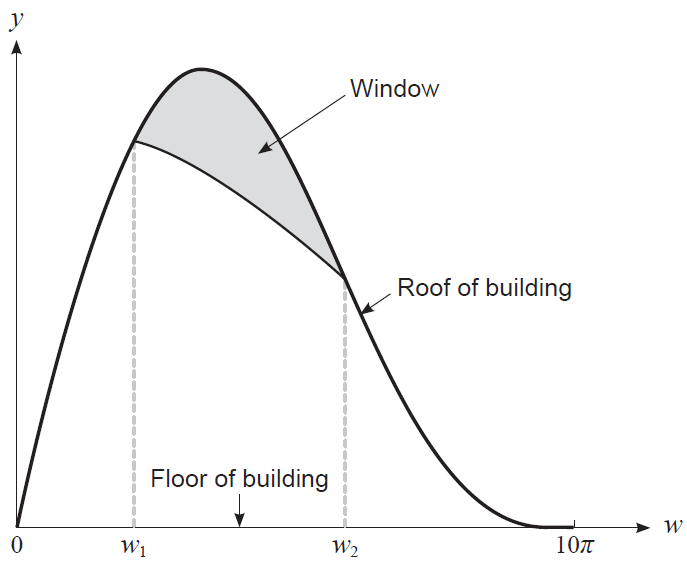
The roof height \(h(w)\) of the building at any point \(w\) along its width is given by \[ h(w) = 6 \sin\left(\frac{w}{10}\right) + 3 \sin\left(\frac{w}{5}\right) \] where \(h\) and \(0 \le w \le 10\pi\) are measured in metres.
(a) Determine the cross-sectional area of the building. (2 marks)
The designer would like to place a window, as shown in the figure above, that is bounded above by the roof of the building and below by the formula \[ g(w) = 7 \cos\left(\frac{w}{20}\right) \]
(b) With reference to the figure
(i) determine the values of \(w_1\) and \(w_2\). (2 marks)
(ii) determine the area of the window. (2 marks)
(c) Use calculus techniques to determine the maximum height of the building. (4 marks)
An object moves from the point (0, 0) along the curve \(y = \sqrt{3} \sin(x)\). The distance, \(D\), travelled along the curve is given by
\[ D(t) = \int_{0}^{\pi t} \sqrt{1 + 3\cos^2(x)} \, dx \]where \(D\) is measured in metres and \(t\) is measured in seconds.
(a) Determine the speed \( s = \frac{dD}{dt} \) of the object when \(t = 1\). (3 marks)
(b) Use the increments formula to estimate the distance travelled by the object between \(t = 1\) and \(t = 1.02\). (2 marks)
End of questions
Integral Calculus Topic Test 10
Section Two: Technology-active
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Let \(f(x)\) be a function such that \(f(-2)=4, f(-1)=0, f(0)=-1, f(1)=0\) and \(f(3)=2\). Further, \(f'(x)<0\) for \(-2 \le x < 0\), \(f'(0)=0\) and \(f'(x)>0\) for \(0 < x \le 3\).
(a) Evaluate the following definite integrals:
(i) \(\int_{-1}^3 f'(x) dx\). (2 marks)
(ii) \(\int_{-2}^3 f'(x) dx\). (2 marks)
(b) What is the area bounded by the graph of \(f'(x)\) and the \(x\) axis between \(x=-2\) and \(x=3\)? Justify your answer. (4 marks)
Consider the function \(f(x) = \ln(x)\). The function \(g(x) = f(x) + a\) is a vertical translation of \(f\) by \(a\) units.
(a) Express the function \(g(x) = \ln(4x)\) in terms of a vertical translation of \(f\) (i.e. in the form \(g(x) = f(x) + a\)), stating the number of units that \(f\) is translated. (2 marks)
The function \(h(x) = cf(x)\) is a vertical dilation of \(f\) by a scale factor of \(c\).
(b) Express the function \(h(x) = \ln(\sqrt{x})\) in terms of a vertical dilation of \(f\), stating the scale factor. (2 marks)
The function \(p(x) = f(bx)\) is a horizontal dilation of \(f\) by a scale factor of \( \frac{1}{b} \).
(c) Express the function \(p(x) = \ln(x) + 4\) in terms of a horizontal dilation of \(f\), stating the scale factor. (3 marks)
End of questions
Integral Calculus Topic Test 11
Section Two: Technology-active
Number of marks: 5
Reading time: 1 minute
Writing time: 5 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
An object moves from the point (0, 0) along the curve \(y = \sqrt{3} \sin(x)\). The distance, \(D\), travelled along the curve is given by
\[ D(t) = \int_{0}^{\pi t} \sqrt{1 + 3\cos^2(x)} \, dx \]
where \(D\) is measured in metres and \(t\) is measured in seconds.
(a) Determine the speed \( s = \frac{dD}{dt} \) of the object when \(t = 1\). (3 marks)
(b) Use the increments formula to estimate the distance travelled by the object between \(t = 1\) and \(t = 1.02\). (2 marks)
End of questions
Integral Calculus Topic Test 12
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Ava is flying a drone in a large open space at a constant height of 5 metres above the ground. She flies the drone due north so that it passes directly over her head and then, sometime later, reverses its direction and flies the drone due south so it passes directly over her again. With \(t=0\) defined as the moment when the drone first flies directly above Ava's head, the velocity of the drone, at time \(t\) seconds, is given by:
\[ v = 2 \sin\left(\frac{t}{3} + \frac{\pi}{6}\right) \text{ m/s } 0 \le t \le 16 \](a) Determine \(x(t)\), the displacement of the drone at \(t\) seconds, where \(x(0)=0\). (3 marks)
(b) Where is the drone in relation to the pilot after 16 seconds? (2 marks)
(c) At a particular time, the drone is heading due south and it is decelerating at 0.5 m/s². How far has the drone travelled from its initial position directly above Ava's head until this particular time? (3 marks)
End of questions


