Question 1 (9 marks) [2021 Section 1 Q1]

(a) Differentiate \( \frac{3x+1}{x^3} \) and simplify your answer. (3 marks)

(b) Let \( f'(x) = x\ln(2x) \). Determine a simplified expression for the rate of change of \( f'(x) \). (3 marks)

(c) Given that \( g'(x) = 4e^{2x} \) and \( g(1) = 0 \), determine \( g(5) \). (3 marks)

Question 2 (10 marks) [2021 Section 1 Q2]

It takes Nahyun between 15 and 40 minutes to get to school each day, depending on traffic conditions. Nahyun leaves home for school at 8:00 am each school day. Let the random variable \(X\) be the time, in minutes after 8:00 am, that Nahyun arrives at school. The probability density function of \(X\) is shown below.

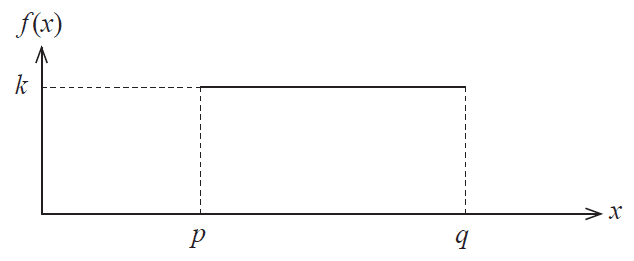
(a) What is the name of this type of distribution? (1 mark)

(b) Determine:

(i) the values of \(p\), \(q\) and \(k\) (2 marks)

(ii) the expected value of \(X\) (1 mark)

(iii) the probability that Nahyun arrives at school before 8:25 am. (2 marks)

Nahyun will be late for her first class if she arrives at school after 8:28 am. Otherwise, she will not be late.

(c) If Nahyun is not late for her first class, what is the probability that she arrives after 8:25 am? (2 marks)

(d) If Nahyun only wants to be late for her first class at most 4% of the time, what time should she leave home, assuming the 15 to 40 minute travel time remains the same? (2 marks)

Question 3 (3 marks) [2021 Section 1 Q3]

Given that \( \ln(2) \approx 0.693 \), use the increments formula to determine an approximation for \( \ln(2.02) \).

Question 4 (7 marks) [2021 Section 1 Q4]

Determine the following:

(a) \( \int (2x^2 - x^3) dx \) (2 marks)

(b) \( \int_{0}^{\frac{\pi}{3}} \frac{\sin(x)}{3 - \cos(x)} dx \) (3 marks)

(c) \( \frac{d}{dy} \int_{-1}^{y} 3x^2 \cos(2x) dx \) (2 marks)

Question 5 (6 marks) [2021 Section 1 Q5]

(a) Determine the area between the parabola \( y = x^2 - x + 3 \) and the straight line \( y = x + 3 \). (4 marks)

(b) The area between the parabola \( y = x^2 - x - 2 \) and the straight line \( y = x - 2 \) is the same as the area determined in part (a). Explain why this is the case. (2 marks)

Question 6 (7 marks) [2021 Section 1 Q6]

(a) The graphs of three normal distributions are displayed below. The distributions have been labelled A, B and C.

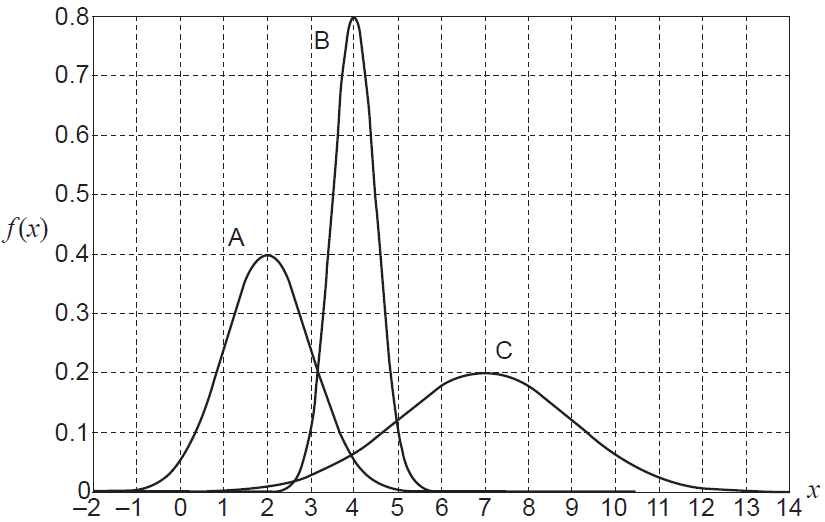
(i) What is the mean of distribution A? (1 mark)

(ii) Which of the distributions has the largest standard deviation? Justify your answer. (1 mark)

(b) A random variable \(X\) is normally distributed. The distribution of \(X\) is graphed below.

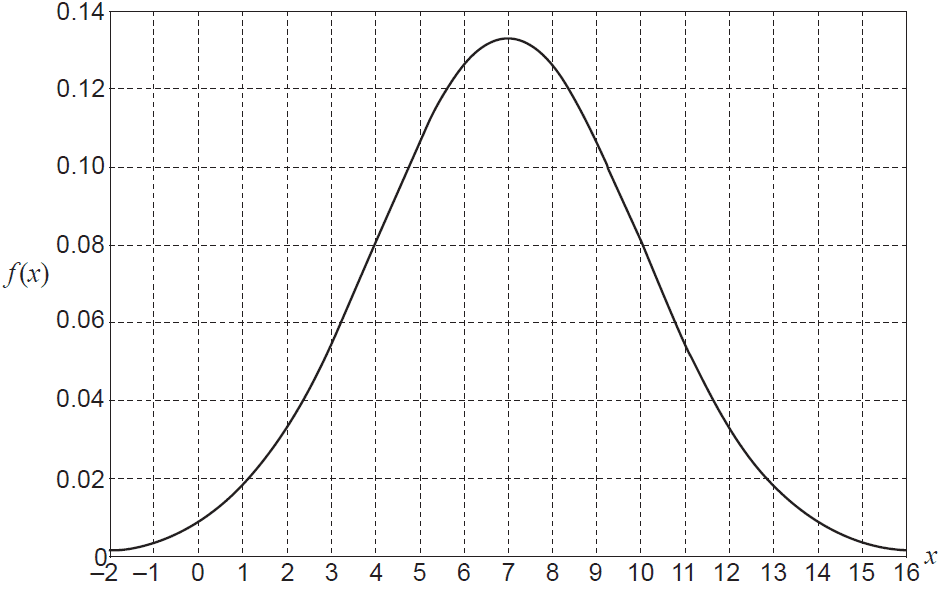
(i) Shade the region with area corresponding to \(P(6 \le X \le 9)\). (1 mark)

(ii) Is \(P(6 \le X \le 9) \ge 0.5\)? Justify your answer. (2 marks)

(c) A random variable \(Y\) has probability \(P(Y \ge 2) > P(Y > 2)\). Explain whether it is possible for the distribution of \(Y\) to be normal or binomial. (2 marks)

Question 7 (9 marks) [2021 Section 1 Q7]

(a) Consider the function \( f(x) = \frac{1}{x} \), graphed twice below.

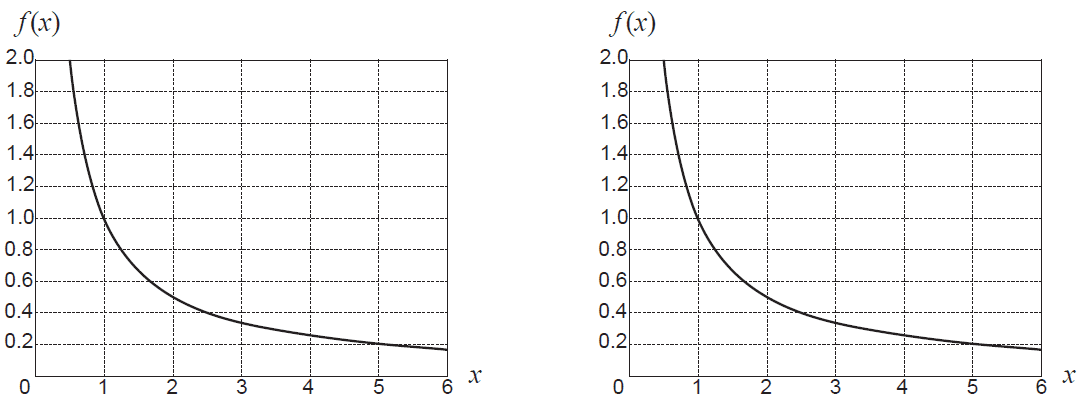
(i) Shade two different regions (one on each graph above) each with area exactly \( \ln(2) \). (2 marks)

(ii) Given that \( \int_{a}^{b} \frac{1}{x} dx = \ln(3) \), what is the relationship between \(a\) and \(b\)? (2 marks)

(b) Another graph of \( f(x) = \frac{1}{x} \) is shown below.

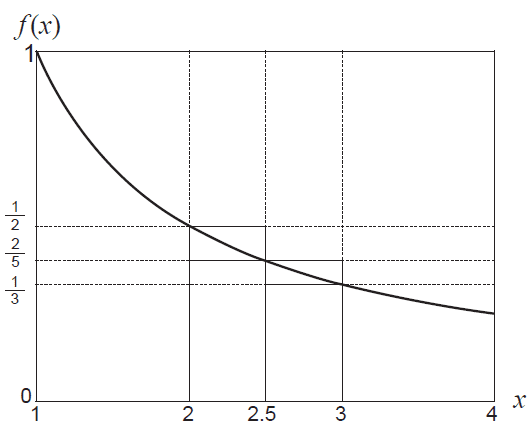
(i) By considering the areas of the rectangles shown, demonstrate and explain why

\[ \frac{11}{30} < \int_{2}^{3} \frac{1}{x} dx < \frac{9}{20} \] (3 marks)

(ii) Hence show that \( \frac{11}{30} < \ln(1.5) < \frac{9}{20} \). (2 marks)

Question 8 (9 marks) [2021 Section 2 Q8]

The weights \(W\) (in grams) of carrots sold at a supermarket have been found to be normally distributed with a mean of 142.8 g and a standard deviation of 30.6 g.

(a) Determine the percentage of carrots sold at the supermarket that weigh more than 155 g. (2 marks)

Carrots sold at the supermarket are classified by weight, as shown in the table below.

Classification	Small	Medium	Large	Extra large
Weight \(W\) (grams)	\(W \le 110\)	\(110 < W \le 155\)	\(155 < W \le 210\)	\(W > 210\)
\(P(W)\)		0.5131	0.3310

(b) Complete the table above, providing the missing probabilities. (2 marks)

(c) Of the carrots being sold at the supermarket that are not of medium weight, what proportion is small? (2 marks)

The supermarket sells bags of mixed-weight carrots, with 12 randomly-selected carrots placed in each bag.

(d) If a customer purchases a bag of mixed-weight carrots, determine the probability that there will be at most two small carrots in the bag. (3 marks)

Question 9 (8 marks) [2021 Section 2 Q9]

The Interesting Architecture company has designed a building with a constant cross-section shown in the figure below.

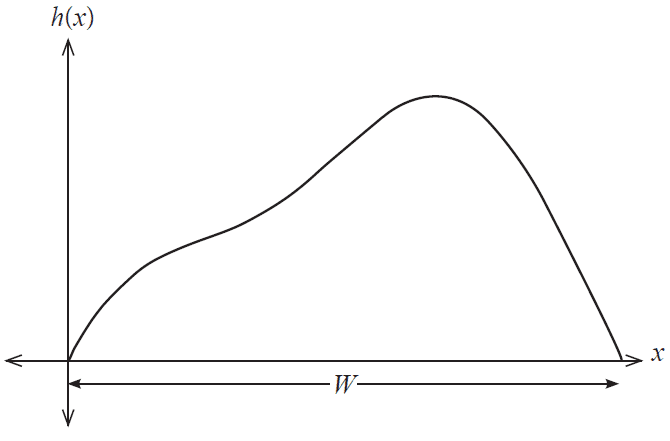
With reference to the figure, the height \(h(x)\) of the building at a point \(x\) along its width is given by

\[ h(x) = 4\sin\left(x - \frac{3\pi}{2}\right) - x^2 + 3\pi x - 4, \text{ where } h \text{ and } 0 \le x \le W \text{ are measured in metres.} \]

(a) Determine the width \(W\) of the building to the nearest centimetre. (2 marks)

(b) Determine \(h'(x)\). (1 mark)

(c) Determine, to the nearest centimetre, the value of \(x\) at which the height of the building is maximum and state this maximum height. (2 marks)

(d) An adventure company allows tourists to climb from the ground on the left of the building, then along the outside of the building to the top. The company installs a platform that allows climbers to rest on their way up to the top. The platform is located on the second half of the climb, at the point where it is the steepest. How high off the ground, to the nearest centimetre, is it positioned? (3 marks)

Question 10 (8 marks) [2021 Section 2 Q10]

A charity organisation has printed 'Lucky 7' scratchie tickets as a fundraiser for use at two special events. The tickets contain two panels. Each ticket has the same numbers as the sample ticket shown below, arranged randomly and hidden within each panel.

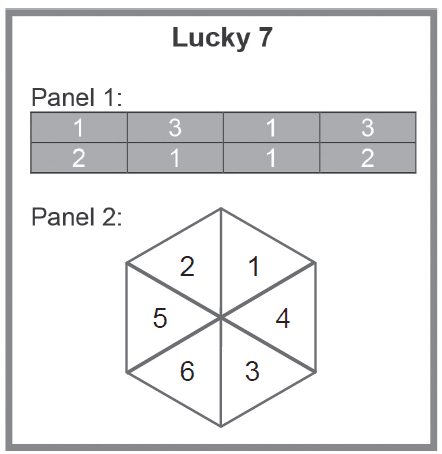
A player scratches one section of each panel to reveal a number. The two numbers revealed are then added together. If the total is seven or higher, the player wins a prize.

At the first event, 400 tickets are purchased, and a prize is won on 124 occasions. Let \(\hat{p}\) denote the probability that a prize is won.

(a) Determine the sample proportion of times that a prize is won at the first event. (1 mark)

(b) Show that the probability \(p\) of winning a prize is \( \frac{7}{24} \). (2 marks)

(c) Calculate the mean and standard deviation of the sample proportion of times a prize is won when 400 tickets are purchased. (2 marks)

(d) At a second event, 400 scratchie tickets are again purchased. If the sample proportion was 0.6 standard deviations from the population proportion, how many prizes were won at the second event? (3 marks)

Question 11 (17 marks) [2021 Section 2 Q11]

A new political party, the Sustainable Energy Party, is planning to have candidates run in the next election. Researchers have collected data that suggests the proportion of voters likely to vote for the party to be 23%.

One year before the next election, random samples of 400 voters were taken in a particular electorate. Let \(\hat{p}\) denote the sample proportion of voters who indicated they would vote for the Sustainable Energy Party at the next election.

(a) State the distribution of \(\hat{p}\). (3 marks)

(b) Calculate the probability that the proportion of voters likely to vote for the Sustainable Energy Party in a sample of 400 is less than 0.20. (3 marks)

One week before the election, researchers believed that the proportion of voters likely to vote for the party in that same electorate had increased. A random sample of 200 voters was taken at this time, and 55 of them indicated they would vote for the Sustainable Energy Party at the next election.

(c) Based on this sample, estimate the proportion of voters likely to vote for the Sustainable Energy Party in this electorate. (1 mark)

(d) For a 99% confidence interval, what is the margin of error of the sample proportion of voters likely to vote for the Sustainable Energy Party in this electorate, based on this sample? (2 marks)

(e) Based on this sample, calculate a 95% confidence interval for the population proportion of voters likely to vote for the Sustainable Energy Party in this electorate. (3 marks)

(f) Based on the research, did the proportion of voters likely to vote for the Sustainable Energy Party in this electorate increase in the year leading up to the election? Justify your answer. (2 marks)

(g) The analysis above models the number of voters likely to vote for the Sustainable Energy Party as binomially distributed. State and discuss the validity of any assumptions for the binomial distribution in this context. (3 marks)

Question 12 (15 marks) [2021 Section 2 Q12]

Let \(f(x) = x^2e^x\).

(a) Show that \( f'(x) = xe^x(x+2) \). (2 marks)

(b) Use calculus to determine all the stationary points of \(f(x)\) and determine their nature. (7 marks)

(c) Determine the coordinates of any points of inflection. (2 marks)

(d) Hence sketch the graph of \(f(x)\), clearly indicating the location of all stationary points and points of inflection. (4 marks)

Question 13 (14 marks) [2021 Section 2 Q13]

A carnival game involves five buckets, each containing 5 blue balls and 15 red balls. A player blindly selects a ball from each bucket and wins the game if they select at least 4 blue balls. Let \(X\) denote the number of blue balls selected.

(a) State the distribution of \(X\), including its parameters. (2 marks)

(b) What is the probability of a player winning the game on any given attempt? (2 marks)

(c) Players are charged $2 for each attempt at the game and offered a $150 prize if they win the game. By providing appropriate numerical justification, explain why this is not a good idea for the carnival organisers. (2 marks)

An observer records the outcome of 100 consecutive games and determines the 90% and 95% confidence intervals for the proportion of wins, \(p\). The confidence intervals are (0.04, 0.16) and (0.05, 0.15).

(d) Which of these intervals is the 95% confidence interval for \(p\)? Justify your answer. (2 marks)

(e) How many wins were observed out of the 100 games? (2 marks)

(f) Determine what you would expect to happen to the width of the confidence intervals if 400 games had been observed. (2 marks)

(g) The true proportion of wins does not lie within either of the above confidence intervals. Does this suggest that a sampling error was made? Justify your answer. (2 marks)

Question 14 (5 marks) [2021 Section 2 Q14]

The displacement in metres, \(x(t)\), of a power boat \(t\) seconds after it was launched is given by:

\[ x(t) = \frac{5t(t^2 - 15t + 48)}{6}, \quad t \ge 0 \]

How far has the power boat travelled before its acceleration is zero?

Question 15 (4 marks) [2021 Section 2 Q15]

The graph of \( y = m\log_3(x-p) + q \) has a vertical asymptote at \( x = 5 \).

(a) Explain why \(p = 5\). (2 marks)

(b) If this graph passes through the points (6, 2) and (14, -6), determine the values of \(m\) and \(q\). (2 marks)

Question 16 (12 marks) [2021 Section 2 Q16]

An analyst was hired by a large company at the beginning of 2021 to develop a model to predict profit. At that time, the company's profit was $4 million. The model developed by the analyst was:

\[ P(x) = \frac{20\ln(x+a)}{x+5}, \]

where \(P(x)\) is the profit in millions of dollars after \(x\) weeks and \(a\) is a constant.

(a) Show that \(a = e\). (2 marks)

(b) What does the model predict the profit will be after five weeks? (1 mark)

(c) Showing use of the quotient rule, determine an equation that, when solved, will give the time when the model predicts the profit will be maximised. (3 marks)

(d) What is this maximum profit and during which week will it occur? (2 marks)

(e) According to the model, during which week will the company's profit fall below its value at the beginning of 2021? (1 mark)

The model proved accurate and after 10 weeks the company implemented some changes. From this time the analyst used a new model to predict the profit:

\[ N(y) = 2e^{b(10+y)}, \]

where \(N(y)\) is the profit in millions of dollars \(y\) weeks from this point in time and \(b\) is a constant.

(f) The company is projecting its profit to exceed $5 million. During which week does the new model suggest this will happen? (3 marks)

Question 17 (8 marks) [2021 Section 2 Q17]

A resort in the Swiss Alps features a cable car that travels from the resort station to the mountain station. Engineers are fixing a cable car that unexpectedly stopped shortly before it reached the mountain station. The engineers are ready to test the cable car. For the purposes of the test, the cable car will initially be at rest in its current position, will head up the mountain, stop at the mountain station and immediately return to the resort station where it will stop, and the test will be complete.

The test begins and engineers believe that the acceleration, \(a(t)\), of the cable car during the test will be: \( a(t) = kt^2 - 23t + 20k \), measured in m/min². The variable \(t\) is the number of minutes from the moment the cable car leaves its position and \(k\) is a constant. After two minutes, the engineers expect that the cable car will be travelling with velocity 18 m/min and will not yet have reached the mountain station.

(a) Determine the value of the constant \(k\). (3 marks)

(b) Once the cable car leaves the mountain station, how long should it take to return to the resort station? (3 marks)

(c) Unfortunately, 10 minutes into the test, the cable car breaks down again. According to the engineers' model, how far is the cable car from the mountain station at this time? (2 marks)