2016 VCE Maths Methods Mini Test 8
Number of marks: 21
Reading time: 3 minutes
Writing time: 31 minutes
Section B – Calculator Allowed
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Express \(\frac{2x+1}{x+2}\) in the form \(a + \frac{b}{x+2}\), where \(a\) and \(b\) are non-zero integers. 2 marks
b. Let \(f: R \setminus \{-2\} \to R, f(x) = \frac{2x+1}{x+2}\).
i. Find the rule and domain of \(f^{-1}\), the inverse function of \(f\). 2 marks
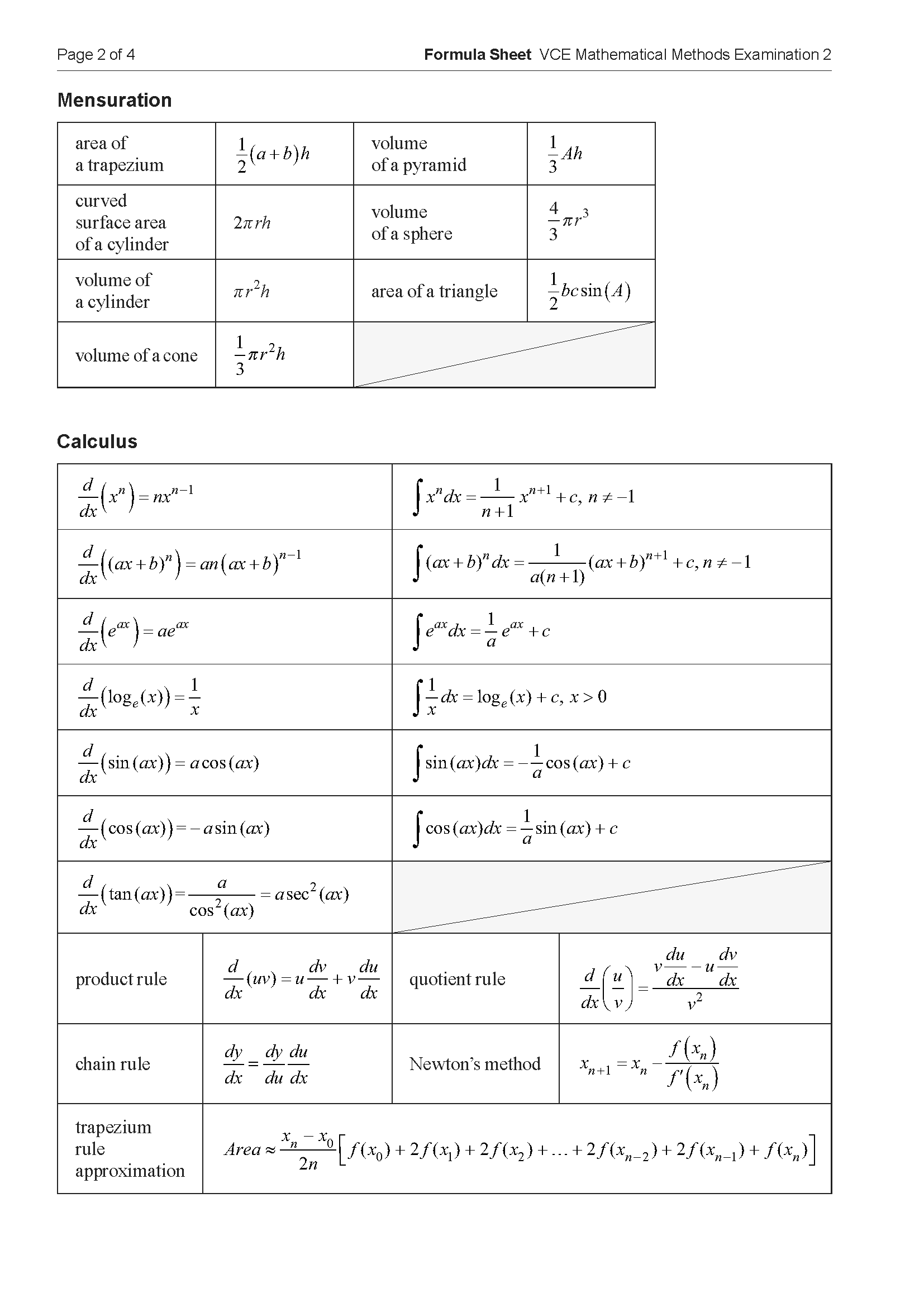
ii. Part of the graphs of \(f\) and \(y = x\) are shown in the diagram below.
Find the area of the shaded region. 1 mark
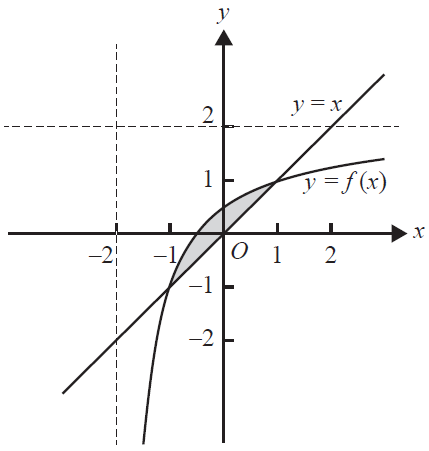
iii. Part of the graphs of \(f\) and \(f^{-1}\) are shown in the diagram below.
Find the area of the shaded region. 1 mark
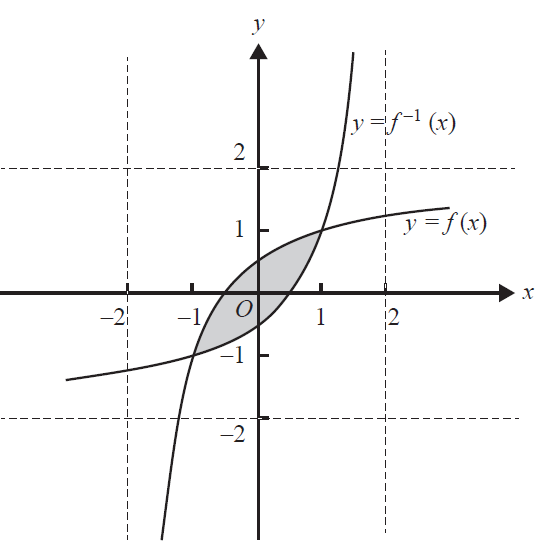
c. Part of the graph of \(f\) is shown in the diagram below.
The point \(P(c, d)\) is on the graph of \(f\).
Find the exact values of \(c\) and \(d\) such that the distance of this point to the origin is a minimum, and find this minimum distance. 3 marks
d. Let \(g: (-k, \infty) \to R, g(x) = \frac{kx+1}{x+k}\), where \(k > 1\).
Show that \(x_1 < x_2\) implies that \(g(x_1) < g(x_2)\), where \(x_1 \in (-k, \infty)\) and \(x_2 \in (-k, \infty)\). 2 marks
e.
i. Let \(X\) be the point of intersection of the graphs of \(y = g(x)\) and \(y = -x\).
Find the coordinates of \(X\) in terms of \(k\). 2 marks
ii. Find the value of \(k\) for which the coordinates of \(X\) are \((-\frac{1}{2}, \frac{1}{2})\). 2 marks
iii. Let \(Z(-1, -1)\), \(Y(1, 1)\) and \(X\) be the vertices of the triangle \(XYZ\). Let \(s(k)\) be the square of the area of triangle \(XYZ\).
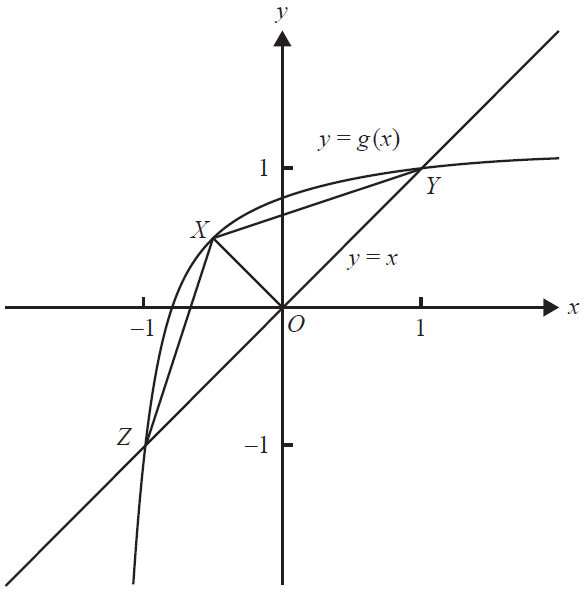
Find the values of \(k\) such that \(s(k) \ge 1\). 2 marks
f. The graph of \(g\) and the line \(y = x\) enclose a region of the plane. The region is shown shaded in the diagram below.
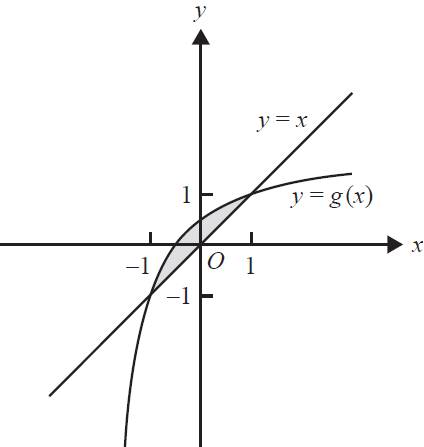
Let \(A(k)\) be the rule of the function \(A\) that gives the area of this enclosed region. The domain of \(A\) is \((1, \infty)\).
i. Give the rule for \(A(k)\). 2 marks
ii. Show that \(0 < A(k) < 2\) for all \(k > 1\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au