2017 VCE Maths Methods Mini Test 7
Number of marks: 10
Reading time: 2 minutes
Writing time: 15 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The function \(f: R \to R, f(x) = x^3 + ax^2 + bx\) has a local maximum at \(x = -1\) and a local minimum at \(x = 3\).
The values of \(a\) and \(b\) are respectively
- A. -2 and -3
- B. 2 and 1
- C. 3 and -9
- D. -3 and -9
- E. -6 and -15
The sum of the solutions of \(\sin(2x) = \frac{\sqrt{3}}{2}\) over the interval \([-\pi, d]\) is \(-\pi\).
The value of \(d\) could be
- A. 0
- B. \(\frac{\pi}{6}\)
- C. \(\frac{3\pi}{4}\)
- D. \(\frac{7\pi}{6}\)
- E. \(\frac{3\pi}{2}\)
Let \(h: (-1, 1) \to R, h(x) = \frac{1}{x-1}\).
Which one of the following statements about \(h\) is not true?
- A. \(h(x)h(-x) = -h(x^2)\)
- B. \(h(x) + h(-x) = 2h(x^2)\)
- C. \(h(x) - h(0) = xh(x)\)
- D. \(h(x) - h(-x) = 2xh(x^2)\)
- E. \((h(x))^2 = h(x^2)\)
The random variable \(X\) has the following probability distribution, where \(0 < p < \frac{1}{3}\).
| \(x\) | -1 | 0 | 1 |
| \(\Pr(X=x)\) | \(p\) | \(2p\) | \(1-3p\) |
The variance of \(X\) is
- A. \(2p(1-3p)\)
- B. \(1-4p\)
- C. \((1-3p)^2\)
- D. \(6p - 16p^2\)
- E. \(p(5-9p)\)
A rectangle \(ABCD\) has vertices \(A(0, 0)\), \(B(u, 0)\), \(C(u, v)\) and \(D(0, v)\), where \((u, v)\) lies on the graph of \(y = -x^3 + 8\), as shown below.
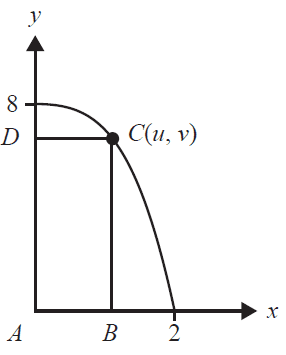
The maximum area of the rectangle is
- A. \(\sqrt[3]{2}\)
- B. \(6\sqrt[3]{2}\)
- C. 16
- D. 8
- E. \(3\sqrt[3]{2}\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Let \(f: [0, \infty) \to R, f(x) = \sqrt{x+1}\).
a. State the range of \(f\). 1 mark
b. Let \(g: (-\infty, c] \to R, g(x) = x^2+4x+3\), where \(c < 0\).
i. Find the largest possible value of \(c\) such that the range of \(g\) is a subset of the domain of \(f\). 2 marks
ii. For the value of \(c\) found in part b.i., state the range of \(f(g(x))\). 1 mark
c. Let \(h: R \to R, h(x) = x^2+3\).
State the range of \(f(h(x))\). 1 mark
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

