2019 VCE Maths Methods Mini Test 5
Number of marks: 9
Reading time: 2 minutes
Writing time: 13 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The discrete random variable \(X\) has the following probability distribution.
| \(x\) | 0 | 1 | 2 | 3 |
| \(\Pr(X=x)\) | \(a\) | \(3a\) | \(5a\) | \(7a\) |
The mean of \(X\) is
- A. \(\frac{1}{16}\)
- B. 1
- C. \(\frac{35}{16}\)
- D. \(\frac{17}{8}\)
- E. 2
An archer can successfully hit a target with a probability of 0.9. The archer attempts to hit the target 80 times. The outcome of each attempt is independent of any other attempt.
Given that the archer successfully hits the target at least 70 times, the probability that the archer successfully hits the target exactly 74 times, correct to four decimal places, is
- A. 0.3635
- B. 0.8266
- C. 0.1494
- D. 0.3005
- E. 0.1701
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
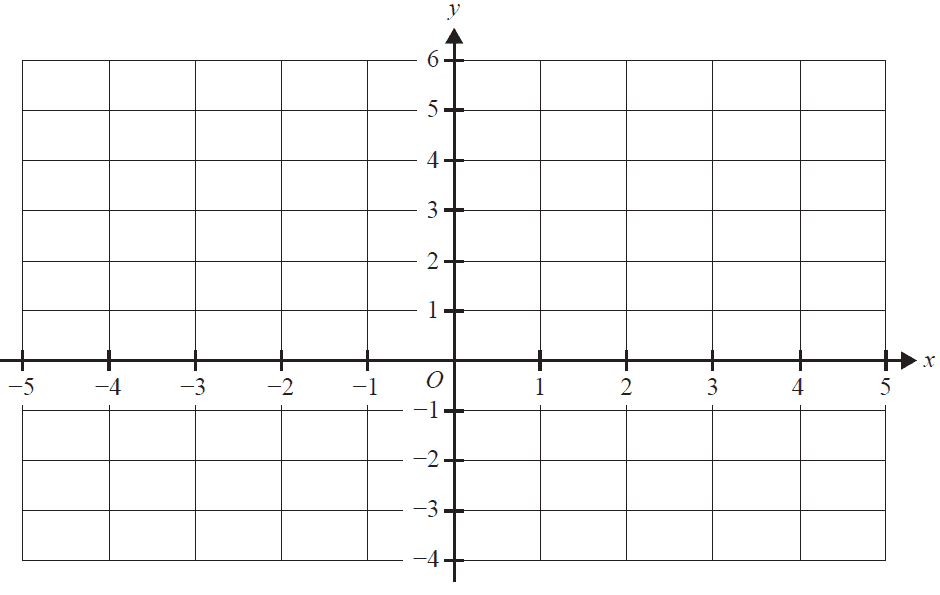
Let \(f: \mathbb{R}\setminus\{1\} \to \mathbb{R}\), \(f(x) = \frac{2}{(x-1)^2} + 1\).
a.
i. Evaluate \(f(-1)\). 1 mark
ii. Sketch the graph of \(f\) on the axes below, labelling all asymptotes with their equations. 2 marks
b. Find the area bounded by the graph of \(f\), the \(x\)-axis, the line \(x=-1\) and the line \(x=0\). 2 marks
Fred owns a company that produces thousands of pegs each day. He randomly selects 41 pegs that are produced on one day and finds eight faulty pegs.
a. What is the proportion of faulty pegs in this sample? 1 mark
b. Pegs are packed each day in boxes. Each box holds 12 pegs. Let \(\hat{P}\) be the random variable that represents the proportion of faulty pegs in a box.
The actual proportion of faulty pegs produced by the company each day is \(\frac{1}{6}\).
Find \(\Pr(\hat{P} < \frac{1}{6})\). Express your answer in the form \(a(b)^n\), where \(a\) and \(b\) are positive rational numbers and \(n\) is a positive integer. 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

