2022 VCAA Maths Methods Exam 1
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 40
Reading time: 15 minutes
Writing time: 1 hours
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Let \( y = 3x e^{2x} \).
Find \( \frac{dy}{dx} \). 1 mark
b. Find and simplify the rule of \( f'(x) \), where \( f : \mathbb{R} \rightarrow \mathbb{R},\ f(x) = \frac{\cos(x)}{e^x} \). 2 marks
a. Let \( g : \left( \frac{3}{2}, \infty \right) \rightarrow \mathbb{R},\ g(x) = \frac{3}{2x - 3} \).
Find the rule for an antiderivative of \( g(x) \). 1 mark
b. Evaluate \( \int_{0}^{1} f(x)\left(2f(x) - 3\right) dx \), where \( \int_{0}^{1} \left[f(x)\right]^2 dx = \frac{1}{5} \) and \( \int_{0}^{1} f(x)\, dx = \frac{1}{3} \). 3 marks
Consider the system of equations
\[ \begin{aligned} kx - 5y &= 4 + k \\ 3x + (k + 8)y &= -1 \end{aligned} \]
Determine the value of \( k \) for which the system of equations above has an infinite number of solutions. 3 marks
A card is drawn from a deck of red and blue cards. After verifying the colour, the card is replaced in the deck. This is performed four times.
Each card has a probability of \( \frac{1}{2} \) of being red and a probability of \( \frac{1}{2} \) of being blue.
The colour of any drawn card is independent of the colour of any other drawn card.
Let \( X \) be a random variable describing the number of blue cards drawn from the deck, in any order.
a. Complete the table below by giving the probability of each outcome. 2 marks
\[ \renewcommand{\arraystretch}{2} \begin{array}{|c|c|c|c|c|c|} \hline x & 0 & 1 & 2 & 3 & 4 \\ \hline \Pr(X = x) & \displaystyle\frac{1}{16} & \rule{0pt}{2.5ex} & \displaystyle\frac{6}{16} & \rule{0pt}{2.5ex} & \rule{0pt}{2.5ex} \\ \hline \end{array} \]
b. Given that the first card drawn is blue, find the probability that exactly two of the next three cards drawn will be red. 1 mark
c. The deck is changed so that the probability of a card being red is \( \frac{2}{3} \) and the probability of a card being blue is \( \frac{1}{3} \).
Given that the first card drawn is blue, find the probability that exactly two of the next three cards drawn will be red. 2 marks
a. Solve \( 10^{3x - 13} = 100 \) for \( x \). 2 marks
b. Find the maximal domain of \( f \), where \( f(x) = \log_e(x^2 - 2x - 3) \). 3 marks
The graph of \( y = f(x) \), where \( f : [0, 2\pi] \rightarrow \mathbb{R},\ f(x) = 2\sin(2x) - 1 \), is shown below.
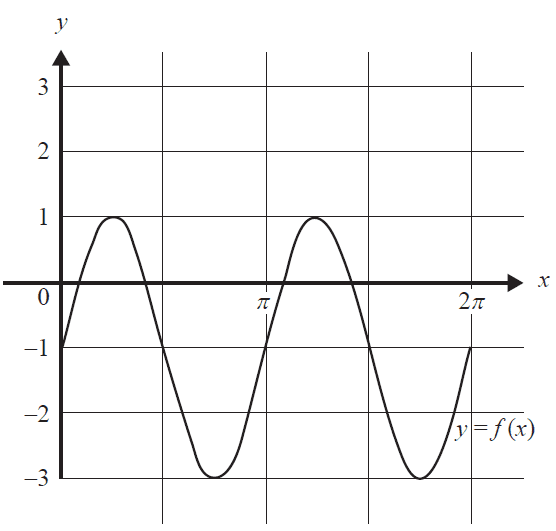
a. On the axes above, draw the graph of \( y = g(x) \), where \( g(x) \) is the reflection of \( f(x) \) in the horizontal axis. 2 marks
b. Find all values of \( k \) such that \( f(k) = 0 \) and \( k \in [0, 2\pi] \). 3 marks
c. Let \( h : D \rightarrow \mathbb{R},\ h(x) = 2\sin(2x) - 1 \), where \( h(x) \) has the same rule as \( f(x) \) with a different domain. The graph of \( y = h(x) \) is translated \( a \) units in the positive horizontal direction and \( b \) units in the positive vertical direction so that it is mapped onto the graph of \( y = g(x) \), where \( a, b \in (0, \infty) \).
i. Find the value for \( b \). 1 mark
ii. Find the smallest positive value for \( a \). 1 mark
iii. Hence, or otherwise, state the domain, \( D \), of \( h(x) \). 1 mark
A tilemaker wants to make square tiles of size 20 cm × 20 cm. The front surface of the tiles is to be painted with two different colours that meet the following conditions:
- • Condition 1 – Each colour covers half the front surface of a tile.
- • Condition 2 – The tiles can be lined up in a single horizontal row so that the colours form a continuous pattern.
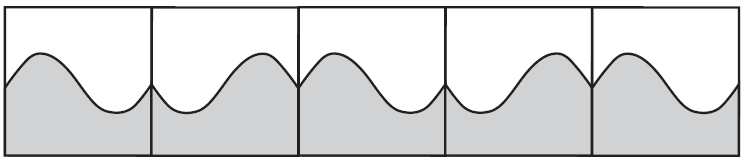
There are two types of tiles: Type A and Type B.
For Type A, the colours on the tiles are divided using the rule \( f(x) = 4 \sin\left(\frac{\pi x}{10}\right) + a \), where \( a \in \mathbb{R} \). The corners of each tile have the coordinates (0, 0), (20, 0), (20, 20) and (0, 20), as shown below.
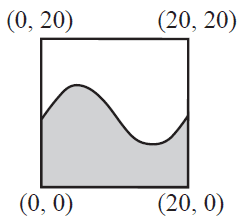
a.
i. Find the area of the front surface of each tile. 1 mark
ii. Find the value of \(a\) so that a Type A tile meets Condition 1. 1 mark
Type B tiles, an example of which is shown below, are divided using the rule \( g(x) = -\frac{1}{100}x^3 + \frac{3}{10}x^2 - 2x + 10 \).
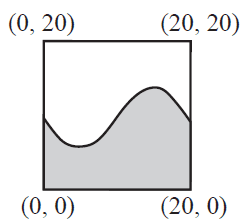
b. Show that a Type B tile meets Condition 1. 3 marks
c. Determine the endpoints of \(f(x)\) and \(g(x)\) on each tile. Hence, use these values to confirm that Type A and Type B tiles can be placed in any order to produce a continuous pattern in order to meet Condition 2. 2 marks
Part of the graph of \(y = f(x)\) is shown below. The rule \(A(k) = k \sin(k)\) gives the area bounded by the graph of \(f\), the horizontal axis and the line \(x = k\).
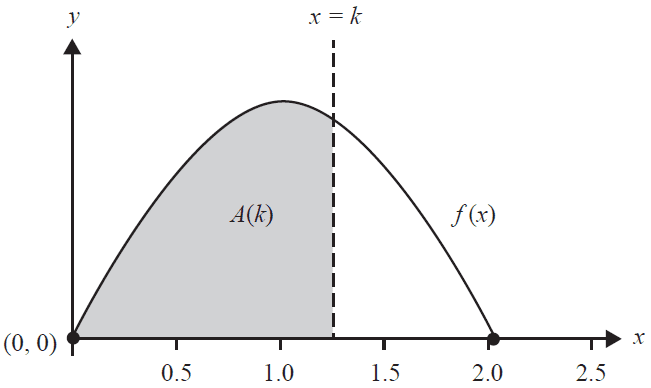
a. State the value of \( A\left(\frac{\pi}{3}\right) \). 1 mark
b. Evaluate \( f\left(\frac{\pi}{3}\right) \). 2 marks
c. Consider the average value of the function \(f\) over the interval \(x \in [0, k]\), where \(k \in [0, 2]\). Find the value of \(k\) that results in the maximum average value. 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

