Question 1 (8 marks) [2023 Section 1 Q1]

(a) Consider the function \(f(x) = x^3e^{2x}\).

(i) Differentiate \(f(x)\). (2 marks)

(ii) Determine the value of \(x\) for any stationary points of \(f(x)\). (3 marks)

(b) Evaluate \( \int_{0}^{\frac{\pi}{4}} \sin(2x + \pi) dx \). (3 marks)

Question 2 (14 marks) [2023 Section 1 Q2]

Let \( p = \ln(2) \), \( q = \ln(3) \) and \( r = \ln(5) \).

(a) Express each of the following in terms of \( p, q \) and/or \( r \).

(i) \( \ln(6) \) (2 marks)

(ii) \( \ln(6.25) \) (3 marks)

(iii) \( \int_{2}^{3} \frac{d}{dx} \ln(x) dx \) (2 marks)

(b) Evaluate \( e^{p+q} \). (2 marks)

(c)

(i) Determine \( \frac{d}{dx}(x \ln(x)) \). (1 mark)

(ii) Hence show that \( \int \ln(x) dx = x \ln(x) - x + c \) where \( c \) is a constant. (2 marks)

(iii) Evaluate \( \int_{1}^{3} \ln(x) dx \) in terms of \( p, q \) and/or \( r \). (2 marks)

Question 3 (10 marks) [2023 Section 1 Q3]

Solcolwa is a green energy company that owns 20 solar farms across Western Australia. The generation capacities, in megawatts (MW), of the solar farms are displayed in the histogram below.

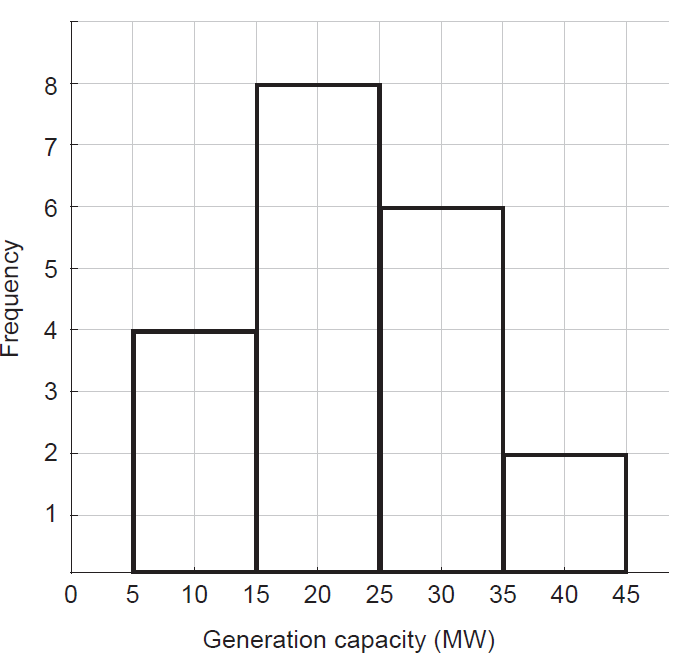
Suppose that one of the Solcolwa solar farms is selected at random. Let the random variable \(W\) denote the generation capacity of the randomly-selected solar farm.

(a) Complete the following table of cumulative probabilities for \(W\). (2 marks)

\(w\)	5	15	25	35	45
\(P(W \le w)\)	0	0.2	0.6	0.9	1

(b) Determine \(P(W \ge 35)\). (1 mark)

(c)

(i) estimate \(P(W \ge 20)\). (2 marks)

(ii) estimate the expected value \(E(W)\). (2 marks)

(d) Given that \(Y = aW\) and that \(W\) and \(Y\) have variances \(\text{Var}(W) = 81\) and \(\text{Var}(Y) = 324\), determine the expected value \(E(Y)\). (3 marks)

Question 4 (8 marks) [2023 Section 1 Q4]

An internet search engine uses a logarithmic scale to rank the importance of internet websites. If a website has \(S\) visits each week, the site rank, \(R\), is given by \[ R = 2\log_{10}\left(\frac{S}{S_0}\right) \] where \(S_0\) is the reference value (the same for all websites). The reference value is the minimum number of visits per week required for a website to register on the site rank scale.

(a) Determine the site rank for a website whose weekly visits are one hundred times the reference value. (2 marks)

(b) Given that a site rank of 12 is assigned to a website with 1.5 billion (\(1.5 \times 10^9\)) visits per week, determine the value of \(S_0\). (3 marks)

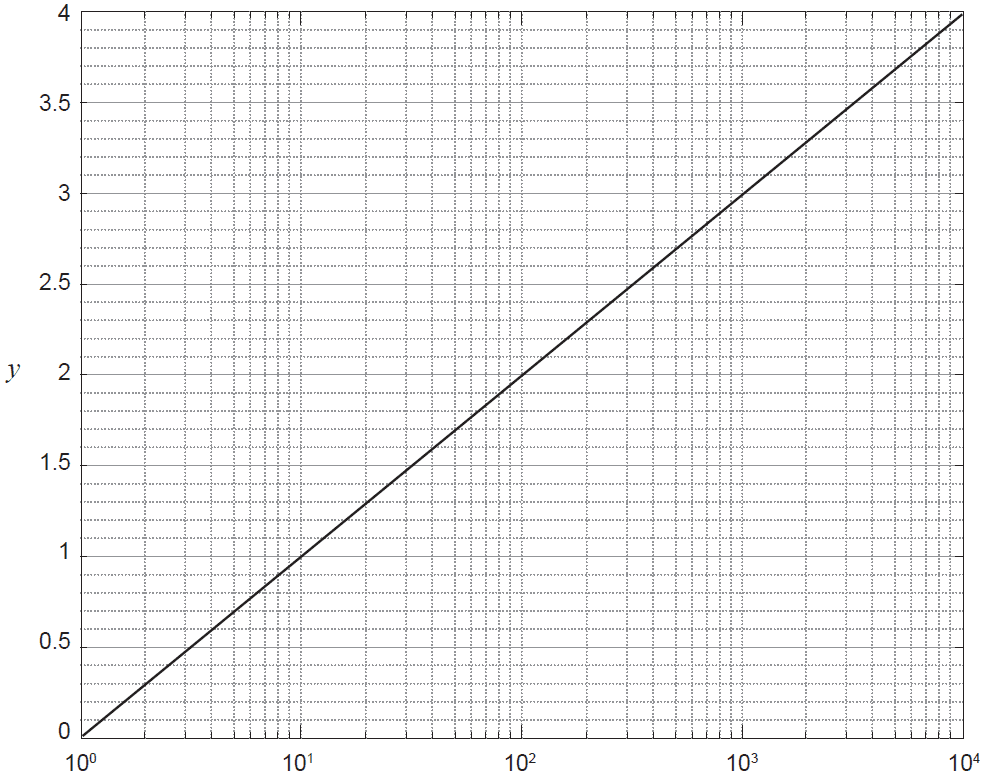
(c) The plot of \(y = \log_{10}(x)\) is shown below. If a website has a site rank of 3.2, use the plot and your answer from part (b) to approximate the website's number of weekly visits. (3 marks)

Question 5 (13 marks) [2023 Section 1 Q5]

The table below contains values of the polynomial function \(f(x)\), its first and second derivatives, and the function \(F(x) = \int_{0}^{x} f(t)dt\) for \(x = 0, 1, 2, 3, 4, 5, 6\).

\(f(x)\) has no stationary points at non-integer values of \(x\), and the letters \(a, b, c, d\) and \(e\) represent unspecified constants.

(a) Evaluate \( \frac{d}{dx}(f(x)^2) \) when \(x = 2\). (2 marks)

(b) Evaluate \( \int_{2}^{4} (f(x)+2) dx \). (3 marks)

(c) Evaluate \( \frac{d}{dx} \int_{2}^{x} f(t) dt \) when \(x=2\). (2 marks)

(d) Determine the x-coordinate of any stationary points and whether they are local maxima, local minima or inflection points. Justify your answer. (3 marks)

(e) Sketch a possible graph of \(f(x)\) for \(0 \le x \le 6\) on the axes below. (3 marks)

Question 6 (11 marks) [2023 Section 2 Q6]

A beekeeper is starting a new colony of bees. The population \(B\) of bees, in thousands, is given by \[ B(t) = 4e^{1.4t} \] where \(t\) is the number of years since the establishment of the colony.

(a) Determine the initial population of the bee colony. (1 mark)

(b) Determine the increase in the population of the bee colony in the first six months. (2 marks)

(c) Determine the rate of population growth two years after the establishment of the colony. (2 marks)

(d) After how many years will the rate of population growth be 65 000 bees/year? (2 marks)

After three years, the beekeeper notices that the number of bees begins to decline. The declining population, \(b\), in thousands, has the form \(b(t) = Ae^{rt}\) where \(t\) is the number of years since the start of the decline.

(e) Determine \(A\) and \(r\) if one year after the start of the decline the bee population is 100 000. (4 marks)

Question 7 (9 marks) [2023 Section 2 Q7]

The Carnaby’s Black Cockatoo is a bird native to southwest Australia. A birdwatcher is interested in estimating the proportion, \(p\), of birds living in a Western Australian national park that are Carnaby’s Black Cockatoos. The birdwatcher visited the national park one morning and, standing at their favourite bird-watching location, observed 200 birds flying past. Seventy-six of those birds were Carnaby’s Black Cockatoos.

(a) On the basis of the sample, determine a point estimate for \(p\). (1 mark)

(b) On the basis of the sample, determine a 95% confidence interval for \(p\). (2 marks)

(c) What is the minimum number of birds that would need to be sampled to ensure that the margin of error of the 95% confidence interval for \(p\) is at most 0.02? (2 marks)

(d) Identify and explain two sources of bias in the birdwatcher’s sampling method. (4 marks)

Question 8 (12 marks) [2023 Section 2 Q8]

An oscillating mass has a velocity, \(v\), given by \[ v(t) = 2t \cos\left(t + \frac{\pi}{2}\right) \quad \text{for } t \ge 0. \] The velocity is given in metres per second, and the time, \(t\), is given in seconds. A graph of the velocity of the mass' motion is shown below.

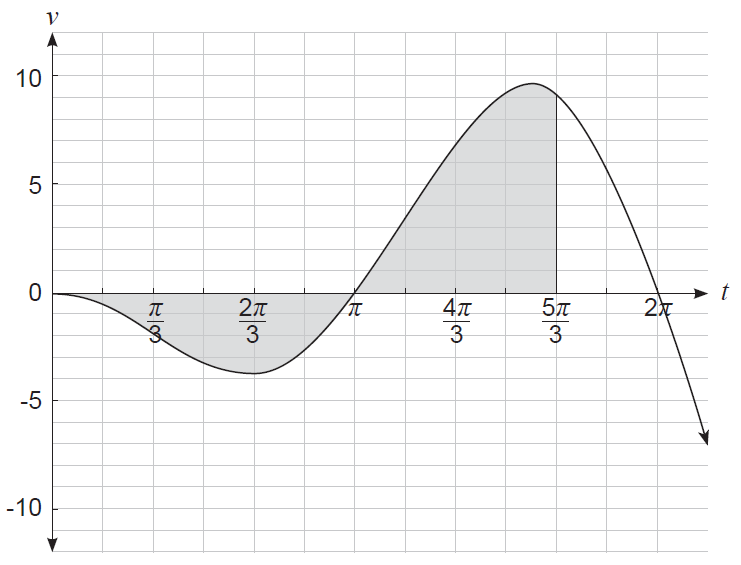
(a) Determine the first two times, \(t > 0\), at which the mass changes direction. State your answers exactly. (2 marks)

(b) What does the signed area of the shaded region in the figure represent? (2 marks)

(c) Write an integral expression for the distance travelled from \(t = \frac{\pi}{3}\) to \(t = \frac{4\pi}{3}\). (3 marks)

(d) Determine the first time after \(t = \pi\) that the acceleration of the object will be 0 m/s\(^2\). (2 marks)

(e) The displacement of the mass is given by \[ x(t) = A \sin\left(t + \frac{\pi}{2}\right) + B \cos\left(t + \frac{\pi}{2}\right) + 2t \sin\left(t + \frac{\pi}{2}\right) \] where \(A\) and \(B\) are constants. Determine the value of \(A\) and \(B\). (3 marks)

Question 9 (10 marks) [2023 Section 2 Q9]

A new entertainment venue is being proposed. The preliminary design has a constant cross-section, as shown in the figure below.

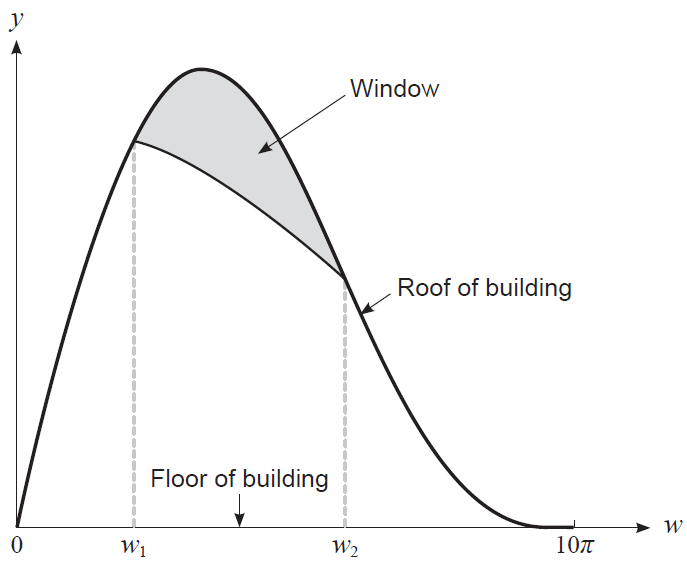
The roof height \(h(w)\) of the building at any point \(w\) along its width is given by \[ h(w) = 6 \sin\left(\frac{w}{10}\right) + 3 \sin\left(\frac{w}{5}\right) \] where \(h\) and \(0 \le w \le 10\pi\) are measured in metres.

(a) Determine the cross-sectional area of the building. (2 marks)

The designer would like to place a window, as shown in the figure above, that is bounded above by the roof of the building and below by the formula \[ g(w) = 7 \cos\left(\frac{w}{20}\right) \]

(b) With reference to the figure

(i) determine the values of \(w_1\) and \(w_2\). (2 marks)

(ii) determine the area of the window. (2 marks)

(c) Use calculus techniques to determine the maximum height of the building. (4 marks)

Question 10 (7 marks) [2023 Section 2 Q10]

Fingerprints can be classified broadly as loop-shaped, whirl-shaped or arch-shaped. Only 5% of the world's population have arch-shaped fingerprints. Consider a random sample of 36 people and let \(\hat{p}\) denote the sample proportion of people with arch-shaped fingerprints. The probability distribution for \(\hat{p}\) is shown below.

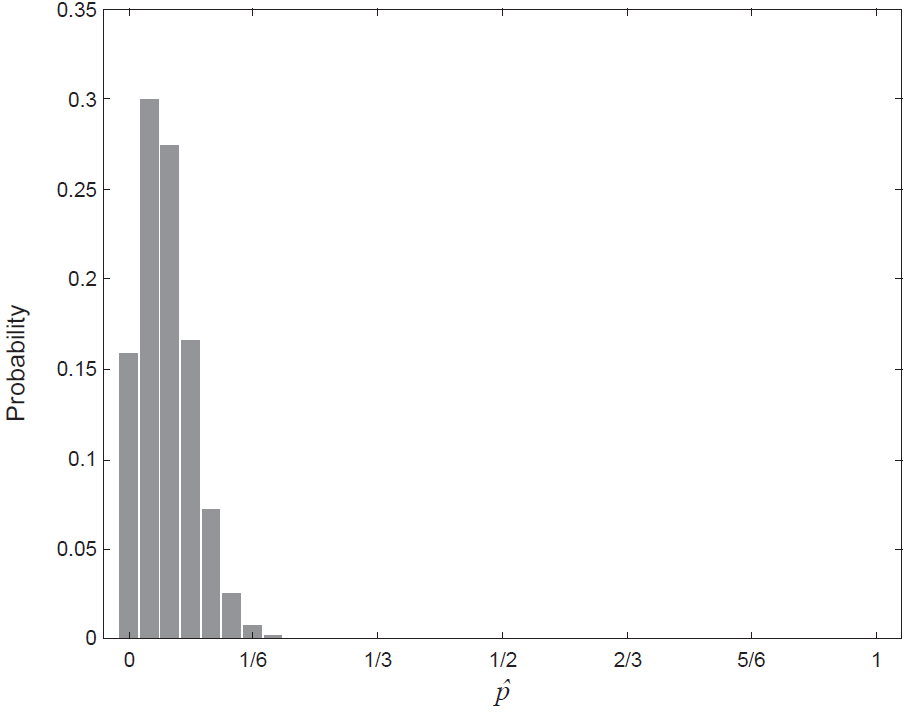
(a) On the basis of the diagram above, is it appropriate to use the normal distribution to approximate the distribution of \(\hat{p}\)? Justify your answer. (2 marks)

A larger sample of 500 people is selected at random.

(b) Determine the probability that more than 30 people in the sample have arch-shaped fingerprints. (3 marks)

(c) Use the approximate normality of the distribution to determine the probability that the sample proportion of people with arch-shaped fingerprints is greater than 0.06. (2 marks)

Question 11 (13 marks) [2023 Section 2 Q11]

Mrs Euler is having her car serviced at BIMDAS Mechanics. She drops her vehicle off at 8 am and is told that her car will be ready for collection at some time between 1 pm and 5 pm that day.

Let the random variable \(B\) denote the time after noon (12 pm) at which a vehicle is ready for collection at BIMDAS Mechanics. The probability density function for \(B\) is shown in the graph below.

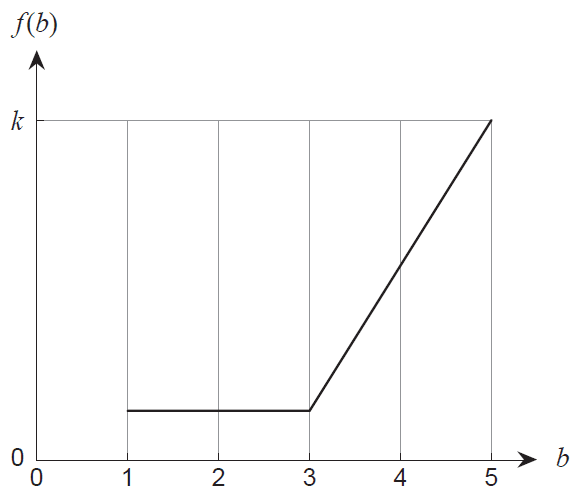
The probability of a vehicle being ready for collection between 2 pm and 3 pm is 0.1.

(a) Determine the value of \(k\). (2 marks)

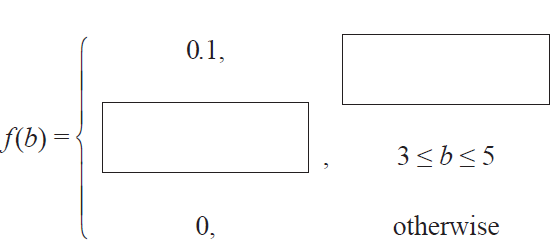
(b) An incomplete expression for the probability density function of \(B\) is given below. Fill in the boxes to complete the missing parts of the expression. (2 marks)

(c) Determine the expected time that Mrs Euler's vehicle will be ready for collection at BIMDAS Mechanics. (3 marks)

Mr Euler is also having his car serviced, but by Addition Autos. He drops his vehicle off at 8 am and is told that his car will be ready for collection at some time between 1 pm and 5 pm that day.

Let the random variable \(A\) denote the time after noon (12 pm) that a vehicle is ready for collection at Addition Autos. The cumulative distribution function for \(A\) is given by \[ P(A \le a) = \begin{cases} 0, & a < 1 \\ \frac{10a - a^2 - 9}{16}, & 1 \le a \le 5 \\ 1, & a > 5 \end{cases} \]

(d) Determine the probability that Mr Euler's vehicle will be ready to collect

(i) by 3 pm. (1 mark)

(ii) between 3 pm and 4 pm. (2 marks)

(e) Determine the expected time at which Mr Euler's vehicle will be ready for collection at Addition Autos. (3 marks)

Question 12 (14 marks) [2023 Section 2 Q12]

A factory produces pre-packed servings of udon noodles. The noodles are dispensed into packets of individual servings by a machine. However, there is variation in the serving sizes dispensed. The specifications attached to the side of the machine have been partially destroyed, so the only available information is that the mass in grams, \(X\), of noodles dispensed is normally distributed, \(P(X \le 150) = 0.0228\) and \(P(X \ge 165) = 0.1587\).

(a) Determine the mean and standard deviation of the mass of noodles dispensed by the machine. (3 marks)

The factory sells trays containing 20 packets of individual servings of udon noodles to restaurants. A standard individual serving should have a mass of at least 150 g.

(b) Determine the probability that a tray of noodles contains no underweight servings. (3 marks)

Following some customer complaints about their serving sizes, the manager of the factory decides to investigate. They select a random sample of 200 individual servings of udon noodles and determine a confidence interval for the proportion \(p\) of underweight servings to be (0.0651, 0.1349).

(c) Determine the margin of error of the confidence interval. (1 mark)

(d) Determine the level of confidence that was used to calculate the confidence interval. (3 marks)

(e) On the basis of the above confidence interval, is the proportion of underweight servings of udon noodles different from what was claimed in the machine specifications? (2 marks)

(f) All else remaining equal, state how the margin of error would change if

(i) the confidence level was decreased. (1 mark)

(ii) the sample size was increased from 200 to 500. (1 mark)

Question 13 (9 marks) [2023 Section 2 Q13]

While leaving a shopping centre a mathematician accidentally drops a bag of apples at the top of a ramp of length 10 m and width 2 m. The diagram below shows the top view of the ramp. Four of the apples roll safely to the end of the ramp, while six roll off an edge and splatter on the ground below.

The mathematician decides to create a simple model by assuming that the:

• apples roll independently of one another along straight lines from the apple drop point
• direction each apple rolls, \(\theta\), is an angle measured about the apple drop point and is uniformly distributed over \(0 \le \theta \le \pi\).

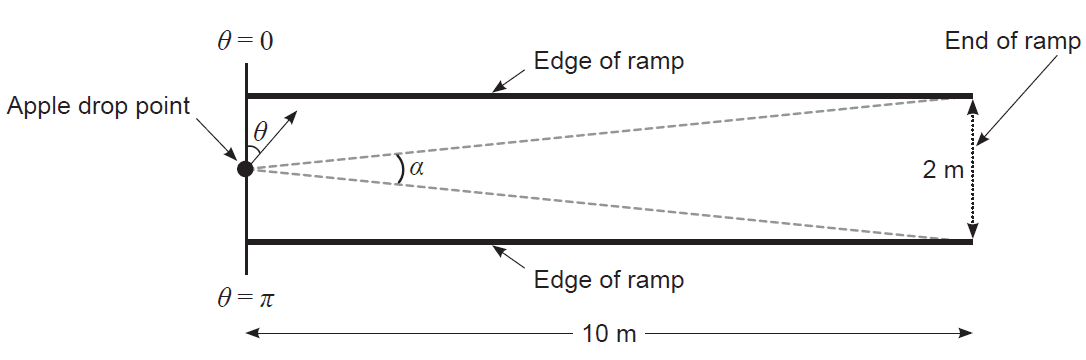
Apples that roll along a line within the sector marked by \(\alpha\) will arrive safely at the end of the ramp, while others will roll off the edge.

(a) (i) Determine the value of \(\alpha\). (2 marks)

(ii) Hence show that the probability, \(p\), of an apple rolling safely to the end of the ramp is \(p = 0.063\) (rounded to three decimal places). (1 mark)

(b) Determine the probability that, of the 10 apples, four or more make it safely to the end of the ramp. (2 marks)

The mathematician decides to purchase another 20 bags of apples, i.e. 200 apples, return to the top of the ramp, and break each bag open one at a time. After the experiment a total of 63 apples have rolled safely to the end of the ramp.

(c) Using the sample of 200 apples, calculate a 99% confidence interval for the population proportion of apples that will roll safely to the end of the ramp. (2 marks)

(d) What does the confidence interval from part (c) suggest about the validity of the model assumptions used to calculate the probability in part (a)(ii)? (2 marks)

Question 14 (11 marks) [2023 Section 2 Q14]

A small dam on an agricultural property has a length of 20 m, and a uniform cross-section shown below where \(x\) and \(y\) are in metres. The base of the dam is flat for \(0 \le x \le 5\), and the right side is given by \(y = \frac{(x-5)^2}{4}\) for \(5 < x \le 11.325\). The shaded region on the graph below represents the cross-section of a volume of water \(V\) (m\(^3\)) in the dam with water level \(h\) (m).

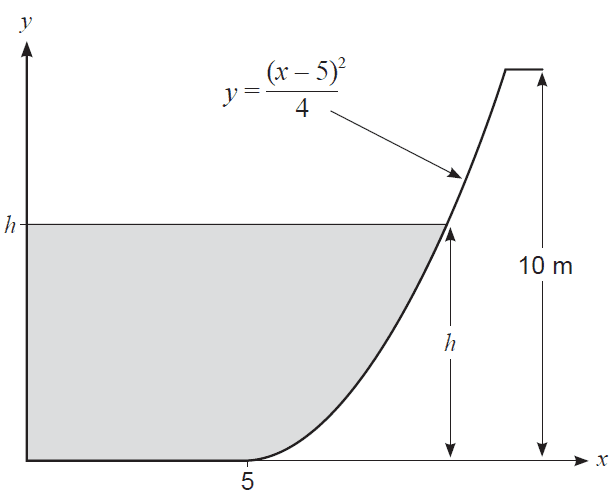
(a) Using calculus, show that the volume of water in the dam is given by \[ V(h) = 100h + \frac{80}{3}h^{\frac{3}{2}} \] (5 marks)

(b) Use the increments formula to estimate the change in water volume if the water level rises from 6 m to 6.1 m. (3 marks)

Suppose the water volume at the start of winter is 1000 m\(^3\). On the basis of rainfall data from previous years, the volume of water \(V_R\) (m\(^3\)) that will flow into the dam over winter is normally distributed with a mean of 600 m\(^3\) and a standard deviation of 200 m\(^3\).

(c) Assuming that there are no other sources of water and no losses, determine the probability that the dam will reach full capacity (i.e. depth of 10 m) during winter. (3 marks)