2022 WACE Maths Methods ATAR Exam Section 1
ATAR course examination. Section One: Calculator-free
This is a full SCSA WACE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official WACE exams split into short tests you can do anytime.
Number of marks: 54
Reading time: 5 minutes
Writing time: 50 minutes
Section One: Calculator-free (54 Marks)
This section has six questions. Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Working time: 50 minutes.
Consider the derivative function \( f'(x) = \frac{4x}{x^2 + 3} \).
(a) Determine the rate of change of \(f'(x)\) when \(x = 1\). (3 marks)
(b) Determine \(f(x)\) given that \(f(1) = \ln(32)\). (4 marks)
(c) Determine \( \frac{d}{dt} \int_{t}^{4} f(x) dx \). (2 marks)
Consider the function \(f(x)\) shown below.
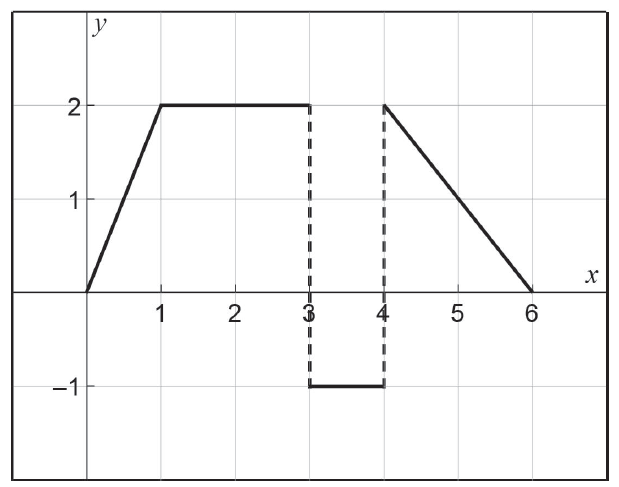
Evaluate the following integrals.
(a) \( \int_{0}^{6} f(x) dx \) (2 marks)
(b) \( \int_{0}^{4} (f(x) - 2) dx \) (2 marks)
(c) \( \int_{4}^{6} f'(x) dx \) (2 marks)
Arnold would like to purchase a toy for his child's birthday. The Isosceles Toy Company claims that the number of weeks until delivery, \(X\), is a random variable whose probability density function is displayed in the graph below.
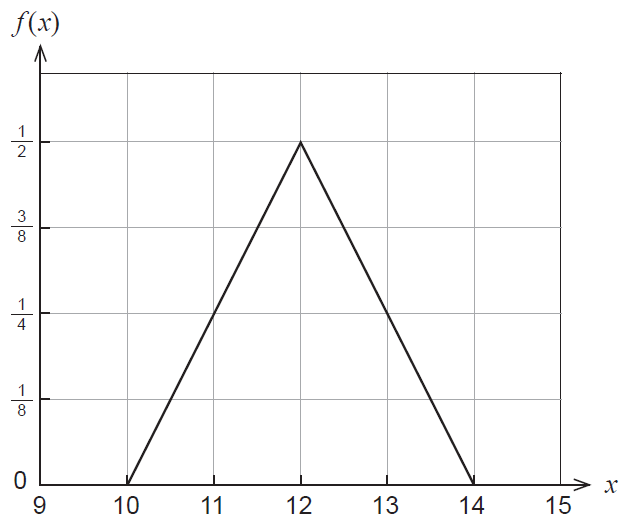
(a) What is the expected time for the toy to be delivered? (1 mark)
His child's birthday is 13 weeks away.
(b) What is the probability that the Isosceles Toy Company will deliver the toy in time for his child's birthday? (2 marks)
(c) Given that the toy arrives in time for his child's birthday, what is the probability that it arrives at least one week early? (2 marks)
Uniform Toys, a rival toy company, claims that the number of weeks until delivery of the same toy, \(Y\), is a random variable whose distribution is displayed in the graph below.
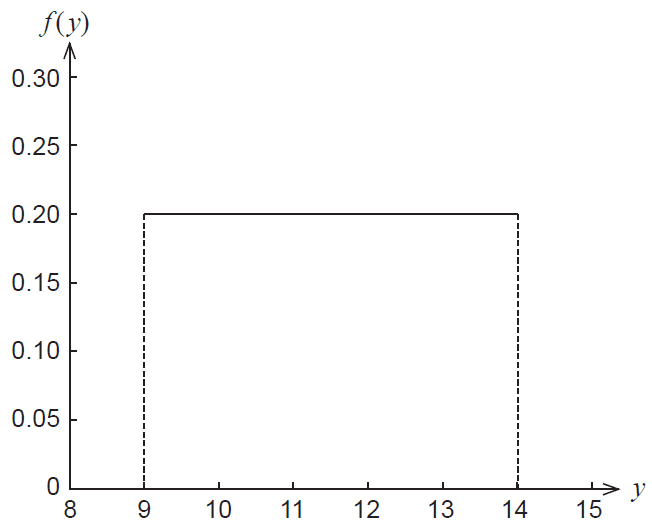
(d) Which toy company should Arnold choose if he would like to maximise the chance that the toy will be delivered in time for his child's birthday? Why? (2 marks)
Suppose that five people order the toy from Uniform Toys and let \(Z\) be a random variable that denotes the number of those people who receive the toy within 13 weeks.
(e) State the distribution for \(Z\). (2 marks)
(f) What is the probability that four out of the five people receive the toy within 13 weeks? (2 marks)
The graph of the function \(f(x) = \log_2(x)\) is shown below.
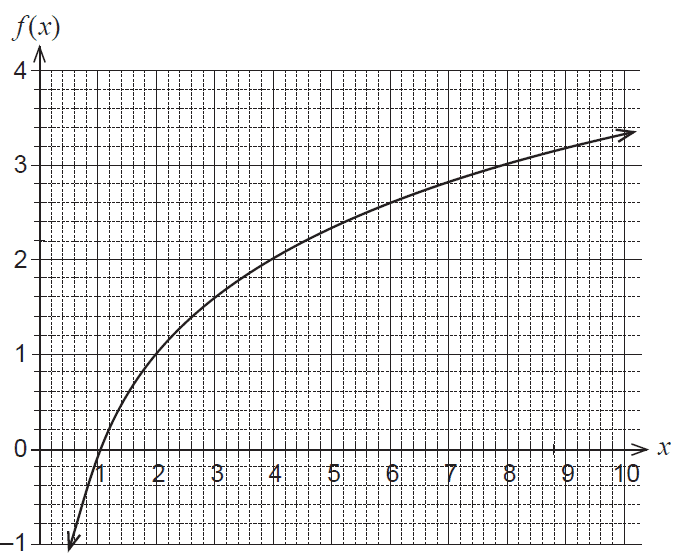
(a) Using the graph:
(i) solve \( \log_2(x-5) = 3 \). (2 marks)
(ii) determine \( \sqrt{7} \), correct to one decimal place. (Hint: let \(x = \sqrt{7}\).) (3 marks)
(b) The function \(f(x) = \log_2(x)\) is translated to give the new function \(g(x)\), which is shown in the graph below.
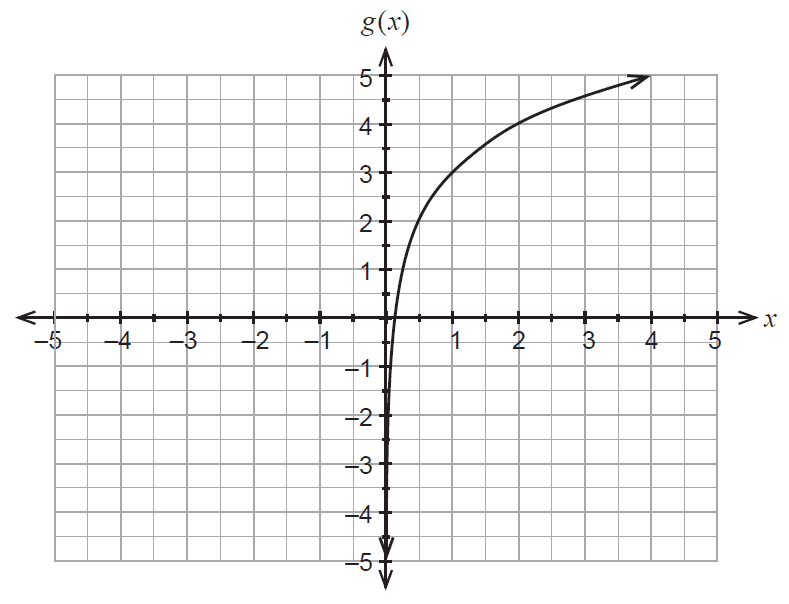
Determine the equation for \(g(x)\). (2 marks)
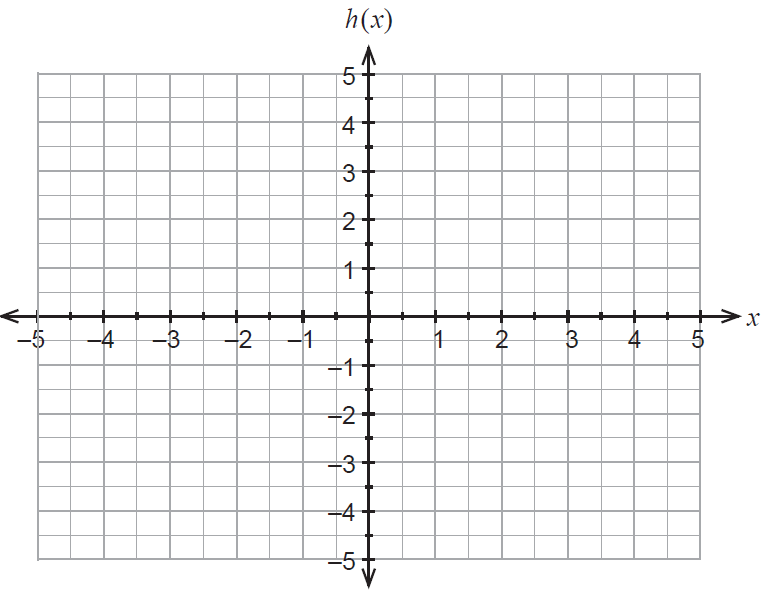
(c)
(i) Show that \( \log_2 \left(\frac{1}{x-1}\right) = -\log_2(x-1) \). (2 marks)
(ii) Hence sketch the graph of \( h(x) = \log_2 \left(\frac{1}{x-1}\right) \) on the axes below. (3 marks)
A continuous function, \(f\), satisfies the following conditions:
- \(f(2) = 0\)
- \(f\) has exactly 2 stationary points
- \(f'(-1) = 0\) and \(f'(1) = 0\)
- \(f''(-1) = 4\)
- \(f'(2) > 0\).
Sketch the function on the axes below.
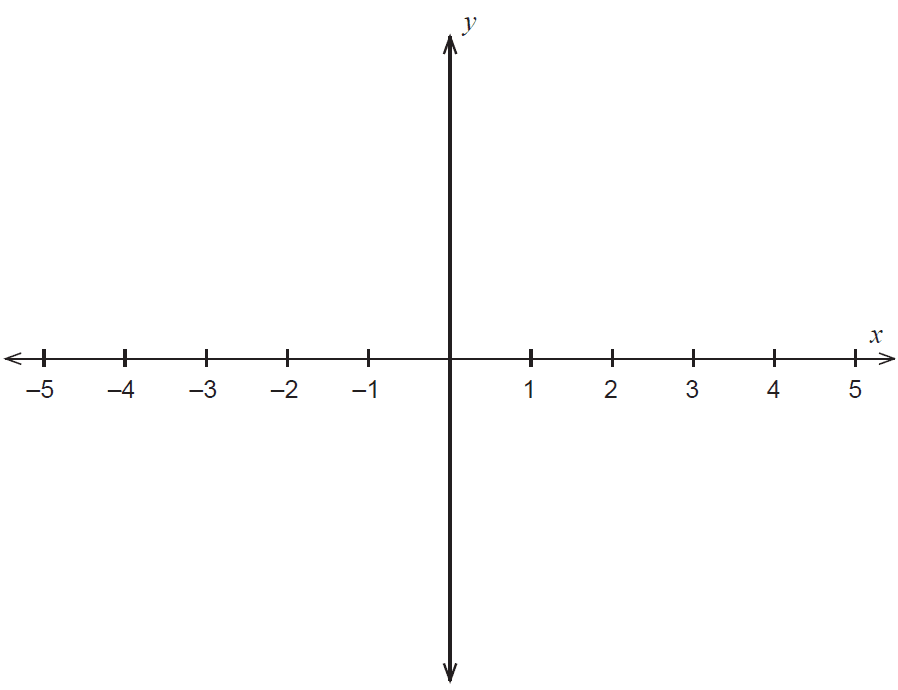
The table of values below may be used to assist you in answering part (b) of this question.
| \(\sin(0) = 0\) | \(\sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\) | \(\sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) | \(\sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\) | \(\sin\left(\frac{\pi}{2}\right) = 1\) |
| \(\cos(0) = 1\) | \(\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\) | \(\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) | \(\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}\) | \(\cos\left(\frac{\pi}{2}\right) = 0\) |
(a)
(i) Determine \( \frac{d}{dx} \left(x \sin\left(\frac{\pi x}{4}\right)\right) \). (2 marks)
(ii) Hence show that
\[ \int \frac{\pi x}{4} \cos\left(\frac{\pi x}{4}\right) dx = x \sin\left(\frac{\pi x}{4}\right) + \frac{4}{\pi} \cos\left(\frac{\pi x}{4}\right) + c \]where \(c\) is a constant. (3 marks)
(b) The time in minutes, \(T\), between incoming phone calls at a call centre is a random variable with probability density function
\[ p(t) = \begin{cases} \frac{\pi}{4} \cos\left(\frac{\pi t}{4}\right) & 0 \le t \le 2 \\ 0, & \text{otherwise} \end{cases} \](i) Determine the probability that the time between two consecutive phone calls is less than 40 seconds. State your answer exactly. (3 marks)
(ii) Use the result from part (a)(ii) to determine the expected time between consecutive phone calls. (3 marks)
END OF PAPER
2022 WACE Maths Methods ATAR Exam Section 2
ATAR course examination. Section Two: Calculator-assumed
This is a full SCSA WACE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official WACE exams split into short tests you can do anytime.
Number of marks: 100
Reading time: 5 minutes
Writing time: 50 minutes
Section Two: Calculator-assumed (100 Marks)
This section has nine questions. Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Working time: 100 minutes.
A team of oceanographers surveyed the depth of the ocean in a region populated by a particular endangered fish species. They discovered a large trench extending below the otherwise flat seabed as shown in the figure below.
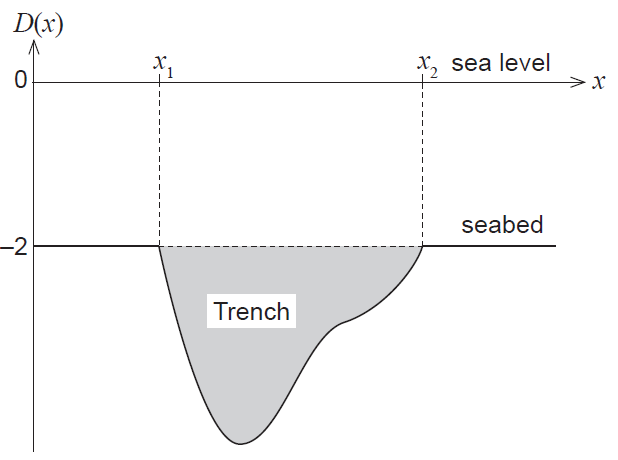
The displacement, in kilometres, from sea level to the ocean floor is given by
\[ D(x) = \begin{cases} (x - 4)^2 + \cos(2x - 3\pi) - 5, & x_1 \le x \le x_2 \\ -2, & \text{otherwise} \end{cases} \]where \(x\) (measured in kilometres) is the east-west horizontal displacement relative to a reference marker at sea level.
(a) With reference to the figure above:
(i) determine the values of \(x_1\) and \(x_2\). (2 marks)
(ii) use calculus to determine the cross-sectional area of the trench shaded in the figure above. (3 marks)
(b) Using calculus, determine the maximum distance of the trench below sea level. (5 marks)
A small outback petrol station receives a weekly delivery of petrol. The volume of petrol sold in a week, \(X\), (in units of 10 000 litres) is a random variable with probability density function
\[ f(x) = 5(1-x)^4, \quad 0 \le x \le 1 \]as shown in the graph below.
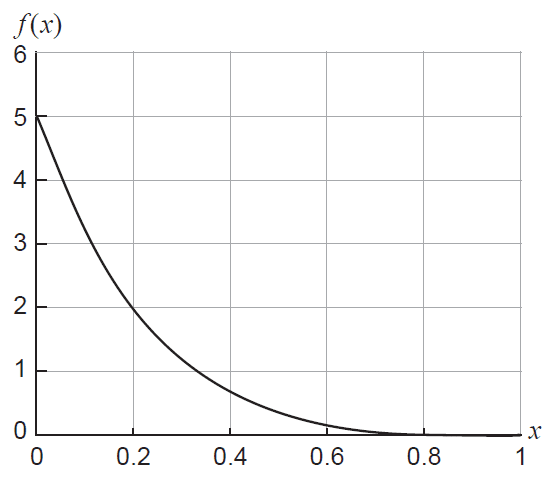
(a) Determine, using appropriate units, the expected value and variance of the amount of fuel sold in a week. (4 marks)
(b) What storage tank capacity will ensure that there is only a 1% chance of running out of petrol in a given week? State your answer to the nearest litre. (3 marks)
(c) When the petrol is delivered, it is pumped into the storage tank. The rate of change of the petrol level in the tank, \(h(t)\), (measured in metres) at time \(t\) (measured in minutes) is given by
\[ h'(t) = \frac{5}{2t+3} \]Determine the height of the storage tank if it takes 20 minutes to fill. (3 marks)
Andrew plans to run a game called Lucky Cup for a school fundraising event. All profits go toward the school's fundraising efforts. The game consists of three standard dice, each placed into a red cup. The red cup is shaken, the dice rolled, and the number of sixes recorded.
Let \(X\) be a random variable denoting the number of sixes rolled in a game of Lucky Cup.
(a) State the distribution of \(X\). (2 marks)
An incomplete probability distribution for \(X\) is shown in the table below.
| \(x\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(P(X=x)\) | \(\frac{125}{216} \approx 0.5787\) |
(b) Complete the table above, providing the missing probabilities. (2 marks)
Lucky Cup costs $1 to play. If a player rolls one 6 they win $1, if they roll two 6s they win $2, and if they roll three 6s they win $3.
(c) Determine the school's expected profit/loss for each game of Lucky Cup. (3 marks)
(d) Determine the probability that a player will make a profit in a game of Lucky Cup. (2 marks)
Andrew wants to increase the attraction of the game by providing the opportunity for larger winnings. He modifies the rules of the game so that players only win money when two or more 6s are rolled, and the winnings for rolling three 6s is three times as much as the winnings for rolling two 6s. Each game still costs $1 to play. He estimates that he should be able to run 500 games and wants to make a profit of $200 for the school.
Andrew calls this game Lucky Cup II.
(e) Determine the winnings Andrew should set for rolling three 6s in Lucky Cup II. (3 marks)
Andrew decides to make the game even more dynamic and exciting. He adds a green cup with a die that he rolls at the beginning of each game. The value that Andrew rolls becomes the target value, and players must roll this target value to win. For example, if Andrew rolls a 2 from the green cup and a player rolls three 2s, the player wins the top prize.
Andrew calls this game Lucky Cup III.
(f) Explain how this change affects a player's chance of winning compared with Lucky Cup II. (2 marks)
The displacement, \(x\), of a mass on the end of a damped spring is given by
\[ x(t) = 3e^{-t} \sin(t), \quad t \ge 0 \]where \(x\) is in centimetres and \(t\) is in seconds.
(a) Determine when the mass first returns to its starting position at \(x = 0\). (2 marks)
(b) Determine an expression for the velocity of the mass. (2 marks)
(c) Determine the displacement of the mass when it first changes direction. (3 marks)
(d) The mass is considered to have stopped oscillating when the oscillation amplitude \(A(t) = 3e^{-t}\) drops to 0.01 cm. How long does it take for the spring to stop oscillating? (2 marks)
The 100 m sprint is a race run on a straight section of track. During a race the velocity, \(v\), measured in metres per second, of an athlete is given by
\[ v(t) = -10e^{-0.8t} - 0.05e^{0.2t} + 10.05 \]where \(t\) is the time, in seconds, measured from the moment the athlete starts to move from the start line.
(a) Determine the acceleration of the athlete three seconds after moving from the start line. (2 marks)
(b) Using calculus, determine the maximum velocity of the athlete during the race, and the time, \(t\), at which it is achieved. (4 marks)
(c) The displacement, \(x\), of the athlete is 0 m at the start of the race. Determine an expression for the displacement of the athlete during the race. (3 marks)
(d) Determine the time, \(t\), at which the athlete finishes the 100 m race. (2 marks)
The Larje Machine Co manufactures metal rods for large industrial equipment. Their standard manufacturing process produces rods whose lengths are normally distributed with a mean of 400 cm, and a standard deviation of 5 cm. A rod is considered 'useable' if its length is between 395 cm and 405 cm.
Let \(X\) be a random variable denoting the length of a rod manufactured by the Larje Machine Co.
(a) Determine the probability that a rod manufactured by the Larje Machine Co is useable. Round your answer to three decimal places. (3 marks)
Recently the Larje Machine Co introduced a new manufacturing process that industry experts claim will improve the percentage of useable rods produced to 80%. The quality control department decides to investigate whether this standard is being achieved and plan to collect a random sample of rods manufactured using the new process.
(b) What condition must the sample satisfy in order to use a normal distribution to model the sample proportion of useable rods? (1 mark)
The quality control department collects a sample of 100 rods.
(c) What is the approximate distribution of the sample proportion of useable rods? (2 marks)
Upon measuring the sample of 100 rods, it is found that 75 are useable.
(d) Calculate a 95% confidence interval for the population proportion of useable rods. (3 marks)
(e) The quality control department would like to obtain a confidence interval with a smaller margin of error. State two methods that it could use to achieve this. (2 marks)
(f) The quality control department decides to select a new sample for which the maximum possible margin of error for a 95% confidence interval is 0.05. What sample size will achieve this requirement? (3 marks)
(g) The new sample yields the 95% confidence interval (0.717, 0.803). On the basis of this sample, is the proportion of useable rods different from what was claimed by the industry experts? Justify your answer. (2 marks)
According to the Association of Poultry Farmers, 35% of people living in Melbourne purchase free-range eggs.
(a) If a random sample of 100 people living in Melbourne is surveyed, what is the probability that the sample proportion of people who purchase free-range eggs will be less than 0.28? (3 marks)
A market research company wants to know whether the proportion \(p\) of people living in Perth who purchase free-range eggs is similar to that of Melbourne. A junior employee proposes that it gather a sample of shoppers by standing outside a particular shop between 9 am and 10 am on a Tuesday morning and asking all shoppers entering the shop if they purchase free-range eggs.
(b) Identify and explain two sources of bias in the proposed sampling method. (4 marks)
The company does not follow the suggestion of the junior employee and instead randomly samples 243 people living in Perth and asks them whether they purchase free-range eggs. On the basis of the results of their survey, a confidence interval for \(p\) is calculated to be (0.2520, 0.3488).
(c) Determine the number of people in the sample who purchase free-range eggs. (2 marks)
(d) Determine the level of confidence that was used to calculate the confidence interval. (3 marks)
The intensity of light travelling through a medium decreases due to scattering and absorption. The intensity of light, \(I\), after travelling a distance of \(x\) centimetres through a soft tissue sample is given by
\[ I = I_0 e^{-0.75x} \]where \(I_0\) is the initial light intensity.
(a) What percentage of the initial light intensity remains after the light has travelled 1 cm through the soft tissue? (2 marks)
(b) After how many centimetres will the light intensity have reached one quarter of its initial value? (2 marks)
(c) Determine an expression for \(\ln\left(\frac{I}{I_0}\right)\) and hence plot \(\ln\left(\frac{I}{I_0}\right)\) versus \(x\) on the axes below. (3 marks)
The intensity of light passing through a different type of soft tissue satisfies the equation
\[ I = I_0 e^{-\mu x} \]where \(\mu\) is the attenuation constant. Light intensity measurements were made on a sample of soft tissue, and the results plotted in the graph below.
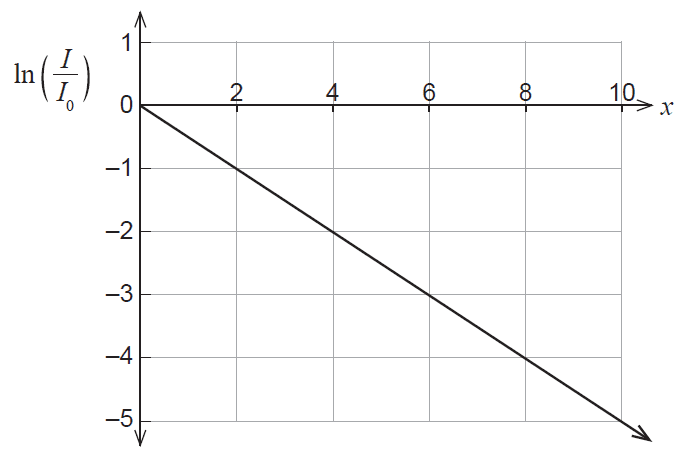
(d) Use the graph to determine the value of the attenuation constant, \(\mu\). (1 mark)
(e)
(i) Express the equation \(I = I_0 e^{-0.75x}\) using base 10 (in the form \(I = I_0 10^{-bx}\)). State the value of \(b\) to three decimal places. (3 marks)
(ii) Describe the change in intensity over a distance of \(\frac{1}{b}\) cm. (2 marks)
An object moves from the point (0, 0) along the curve \(y = \sqrt{3} \sin(x)\). The distance, \(D\), travelled along the curve is given by
\[ D(t) = \int_{0}^{\pi t} \sqrt{1 + 3\cos^2(x)} \, dx \]where \(D\) is measured in metres and \(t\) is measured in seconds.
(a) Determine the speed \( s = \frac{dD}{dt} \) of the object when \(t = 1\). (3 marks)
(b) Use the increments formula to estimate the distance travelled by the object between \(t = 1\) and \(t = 1.02\). (2 marks)
END OF PAPER
WACE is a registered trademark of the School Curriculums and Standards Authority. The SCSA does not endorse or make any warranties regarding this study resource. Past WACE exams and related content can be accessed directly at www.senior-secondary.scsa.wa.edu.au


