Question 1 (6 marks) [2020 Section 1 Q1]

Ashley and Xavier are playing a board game that requires them to use the spinner shown below.

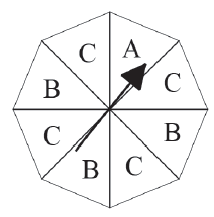
The player spins the arrowhead and the result is where the arrowhead is pointing when it stops moving. The above diagram is showing a result of A.

(a) If the spinner is spun three times, what is the probability that B is never a result? (1 mark)

Let the random variable \(X\) be defined as the number of times B is the result when the spinner is spun three times.

(b) Complete the table below showing the probability distribution of \(X\). (3 marks)

\(x\)	0	1	2	3
\(P(X=x)\)

(c) Determine the mean and variance of the above distribution. (2 marks)

Question 2 (4 marks) [2020 Section 1 Q2]

If \( h(x) = \frac{e^{-x}}{\cos x} \), then evaluate \( h'(\pi) \).

Question 3 (7 marks) [2020 Section 1 Q3]

The graph of the cubic function \( f(x) = ax^3 + bx^2 + cx + d \) is shown below. A turning point is located at (1, 0) and the shaded region shown on the graph has an area of \( \frac{3}{2} \) units².

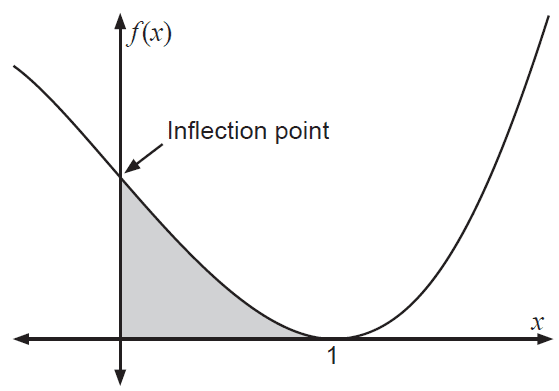
Use the above information to determine the values of \(a\), \(b\), \(c\) and \(d\).

Question 4 (9 marks) [2020 Section 1 Q4]

The heights reached by a species of small plant at maturity are measured by a team of biologists. The results are shown in the histogram of relative frequencies below.

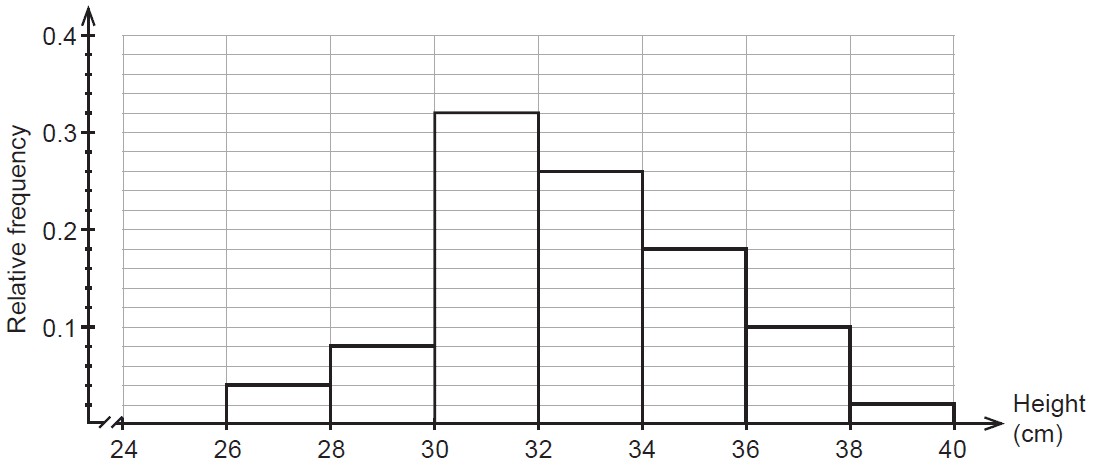
(a) Determine the probability that a mature plant of this species reaches no higher than 30 cm. (1 mark)

(b) If a mature plant reaches a height of at least 32 cm, what is the probability that its height reaches above 38 cm? (2 marks)

Another team of biologists is studying the mature heights of a species of hedge. The height, \(h\) metres, has a probability density function, \(d(h)\), as given below.

\[ d(h) = \begin{cases} \frac{h-1}{5} & \text{for } 1 \le h \le 2 \\ kh^2 & \text{for } 2 < h \le 4 \\ 0 & \text{otherwise} \end{cases} \]

(c) What percentage of hedges from this study reaches a mature height less than 2 m? (3 marks)

(d) Determine the value of \(k\). (3 marks)

Question 5 (5 marks) [2020 Section 1 Q5]

The graphs of the functions \(f\) and \(g\) are displayed below.

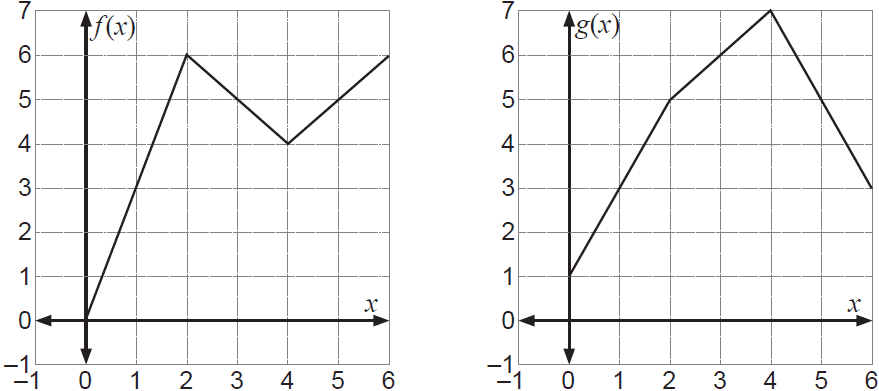
(a) Evaluate the derivative of \(f(x)\) at \(x = 3\). (1 mark)

(b) Evaluate the derivative of \(f(x)g(x)\) at \(x = 5\). (2 marks)

(c) Evaluate the derivative of \(f(g(x))\) at \(x = 1\). (2 marks)

Question 6 (7 marks) [2020 Section 1 Q6]

Consider the function \(f(x) = \ln(x)\). The function \(g(x) = f(x) + a\) is a vertical translation of \(f\) by \(a\) units.

(a) Express the function \(g(x) = \ln(4x)\) in terms of a vertical translation of \(f\) (i.e. in the form \(g(x) = f(x) + a\)), stating the number of units that \(f\) is translated. (2 marks)

The function \(h(x) = cf(x)\) is a vertical dilation of \(f\) by a scale factor of \(c\).

(b) Express the function \(h(x) = \ln(\sqrt{x})\) in terms of a vertical dilation of \(f\), stating the scale factor. (2 marks)

The function \(p(x) = f(bx)\) is a horizontal dilation of \(f\) by a scale factor of \( \frac{1}{b} \).

(c) Express the function \(p(x) = \ln(x) + 4\) in terms of a horizontal dilation of \(f\), stating the scale factor. (3 marks)

Question 7 (13 marks) [2020 Section 1 Q7]

Consider the function \(f(x) = e^{2x} - 4e^x\).

(a) Determine the coordinates of the x-intercept(s) of \(f\). You may wish to consider the factorised version of \(f: f(x) = e^x(e^x - 4)\). (3 marks)

(b) Show that there is only one turning point on the graph of \(f\), which is located at \((\ln(2), -4)\). (3 marks)

(c) Determine the coordinates of the point(s) of inflection of \(f\). (3 marks)

(d) Sketch the function \(f\) on the axes below, labelling clearly all intercepts, the turning point and point(s) of inflection. Some approximate values of the natural logarithmic function provided in the table below may be helpful. (4 marks)

\(x\)	1	2	3	4
\(\ln(x)\)	0	0.7	1.1	1.4

Question 8 (7 marks) [2020 Section 2 Q8]

The weight, \(X\), of chicken eggs from a farm is normally distributed with mean 60 g and standard deviation 5 g. Eggs with a weight of more than 67 g are classed as 'jumbo'.

(a) What proportion of eggs from the farm are 'jumbo'? (2 marks)

(b) What proportion of 'jumbo' eggs are less than 75 g in weight? (3 marks)

(c) The heaviest 0.05% of eggs fetch a higher price. What is the minimum weight of these eggs? (2 marks)

Question 9 (8 marks) [2020 Section 2 Q9]

A cake shop makes birthday cakes. The probability distribution of the number of birthday cakes sold in a day, \(X\), is given below.

\(x\)	0	1	2	3	4
\(P(X=x)\)	0.1	0.2	0.25	0.35	0.1

(a) Calculate the mean number or birthday cakes sold in a day. (1 mark)

(b) On Monday, the cake shop makes four birthday cakes. If each birthday cake costs $20 to make and sells for $50, what is the expected profit or loss on that day? (3 marks)

On Tuesday, the shop makes three birthday cakes. Let the random variable \(\hat{Y}\) denote the number of birthday cakes not sold on that day.

(c) Explain why \(P(\hat{Y}=0) = 0.45\). (2 marks)

(d) Obtain the probability distribution of \(\hat{Y}\). (2 marks)

Question 10 (7 marks) [2020 Section 2 Q10]

Water flows into a bowl at a constant rate. The water level, \(h\), measured in centimetres, increases at a rate given by

\[ h'(t) = \frac{4t+1}{2t^2+t+1} \]

where the time \(t\) is measured in seconds.

(a) Determine the rate that the water level is rising when \(t=2\) seconds. (1 mark)

(b) Explain why \(h(t) = \ln(2t^2+t+1) + c\). (2 marks)

(c) Determine the total change in the water level over the first 2 seconds. (1 mark)

The bowl is filled when the water level reaches \(\ln(56)\) cm.

(d) If the bowl is initially empty, determine how long it takes for the bowl to be filled. (3 marks)

Question 11 (9 marks) [2020 Section 2 Q11]

The line \(y=x+c\) is tangent to the graph of \(f(x)=e^x\).

(a) Obtain the coordinates of the point of intersection of the tangent with the graph of \(f(x)\). (2 marks)

(b) What is the value of \(c\)? (1 mark)

(c) Sketch the graph of \(f(x)\) and the tangent on the axes below. (1 mark)

(d) Evaluate the exact area between the graph of \(f(x)\), the tangent line, and the line \(x=\ln 2\). (3 marks)

(e) Given that \(g(x)\) is the inverse function of \(f(x)\), write a definite integral that could be used to determine the area between the graph of \(g(x)\), the x-axis, and the line \(x=\ln 2\). (2 marks)

Question 12 (21 marks) [2020 Section 2 Q12]

It is estimated that 20% of small businesses fail in the first year. A business advisory group takes a random sample of 500 new businesses that started in January 2018. An analyst employed by the group suggests the use of the binomial distribution is appropriate in this case.

(a) What is the probability that at most 120 of the businesses fail in the first year? (2 marks)

(b) What is the approximate distribution of the sample proportion of small businesses that fail by the end of the year in this sample? Justify your answer. (3 marks)

(c) What is the probability that the sample proportion of businesses that fail by the end of the year is less than 0.18? (2 marks)

(d) By January 2019, 90 of the 500 new businesses had failed. Calculate a 95% confidence interval for the proportion of new businesses that fail in the first year. (2 marks)

The business advisory group believes that the proportion of new businesses that fail within a year can be reduced by providing financial advice. They took another random sample of 500 businesses that started in January 2019 and provided them with regular financial advice. In this random sample, at the end of the year 80 businesses had failed.

(e) Calculate the sample proportion and its margin of error at the 95% confidence level. (2 marks)

(f) Calculate a 95% confidence interval for the proportion of businesses that failed. What do you conclude regarding the value of the financial advice provided to the new businesses? (4 marks)

(g) If the sample size was reduced, what would be the effect on the confidence interval? Justify your answer. (2 marks)

(h) State two assumptions that the analyst made in recommending the use of the binomial model in this case and discuss whether they are valid. (4 marks)

Question 13 (7 marks) [2020 Section 2 Q13]

A company manufactures small machine components. They can manufacture up to 200 of a particular component in one day. The total cost, in hundreds of dollars, incurred in manufacturing the components is given by: \( C(x) = \frac{x \ln(2x+1)}{3} - 2x + 120 \), where \(x\) is the number of components that will be produced on that day.

(a) Determine the total cost of manufacturing 20 components in one day. (1 mark)

(b) On the axes below, sketch the graph of \(C(x)\). (3 marks)

(c) With reference to your graph in part (b), explain how many components the company should manufacture per day if the total cost is to be as low as possible. (3 marks)

Question 14 (10 marks) [2020 Section 2 Q14]

A suburban council hires a consultant to estimate the proportion of residents of the suburb who use its library.

(a) The consultant decides to estimate a 95% confidence interval for the proportion to within an error of 0.01. What minimum sample size should be selected? (3 marks)

(b) If resource limitations dictate that the maximum sample size that can be managed is 500, what is the maximum margin of error in estimating a 99% confidence interval? (3 marks)

The consultant decides to select the sample by standing on the roadside outside the library at lunchtime and asking a random sample of the passers-by whether they use the library.

(c) Identify and explain two possible sources of bias with this sampling scheme. (4 marks)

Question 15 (9 marks) [2020 Section 2 Q15]

A chef needs to use an oven to boil 100 mL of water in five minutes for a new experimental recipe. The temperature of the water must reach 100 °C in order to boil. The temperature, \(T\), of 100 mL of water \(t\) minutes after being placed in an oven set to \(T_0\) °C can be modelled by the equation below.

\[ T(t) = T_0 - 175e^{-0.07t} \]

In a preliminary experiment, the chef placed a 100 mL bowl of water into an oven that had been heated to \(T_0 = 200\) °C.

(a) What is the temperature of the water at the moment it is placed into the oven? (1 mark)

(b) What is the temperature of the water five minutes after being placed in the oven? (1 mark)

(c) What change could be made to the temperature at which the oven is set in order to achieve the five-minute boiling requirement? (2 marks)

Assume that \(T_0\) is still 200 °C.

(d) Determine the rate of increase in temperature of the water five minutes after being placed in the oven. Give your answer rounded to two decimal places. (2 marks)

(e) Explain what happens to the rate of change in the temperature of the water as time increases and how this relates to the temperature of the water. (3 marks)

Question 16 (7 marks) [2020 Section 2 Q16]

A large refrigerator in a scientific laboratory is always required to maintain a temperature between 0 °C and 1 °C to preserve the integrity of biological samples stored inside. A scientist working in the laboratory suspects that the refrigerator is not maintaining the required temperature and decides to record the temperature every hour for seven days. Based on these measurements, the scientist concludes that the temperature, \(T\), in the refrigerator is normally distributed with a mean of 0.8 °C and a standard deviation of 0.4 °C.

(a) Temperature in degrees Fahrenheit, \(T_F\), is given by \(T_F = \frac{9}{5}T + 32\). Determine the mean and standard deviation of the refrigerator temperature in degrees Fahrenheit. (2 marks)

(b) Determine the probability that the refrigerator temperature is above 1 °C. Give your answer rounded to four decimal places. (1 mark)

The histogram of data gathered by the scientist is shown below. \(N\) denotes the number of observations in each temperature interval.

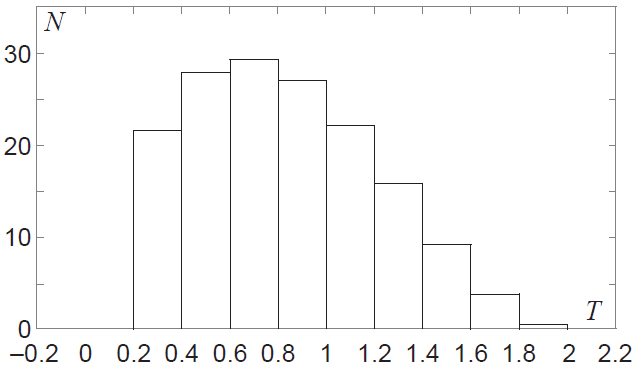
(c) Do you agree that the normal distribution was an appropriate model to use? Provide a reason to justify your response. (2 marks)

An alternative probability density function proposed to model the refrigerator temperature, in degrees Celcius, is given by:

\[ p(t) = \frac{3}{4}t^3 - 3t^2 + 3t, \quad 0 \le t \le 2 \]

(d) Determine the probability that the refrigerator temperature is above 1 °C using the new model. (2 marks)

Question 17 (12 marks) [2020 Section 2 Q17]

David and Katrina have a small farm and wish to fence off an area of their land so they can raise sheep. The area they have chosen has one border along a road as shown in the diagram below.

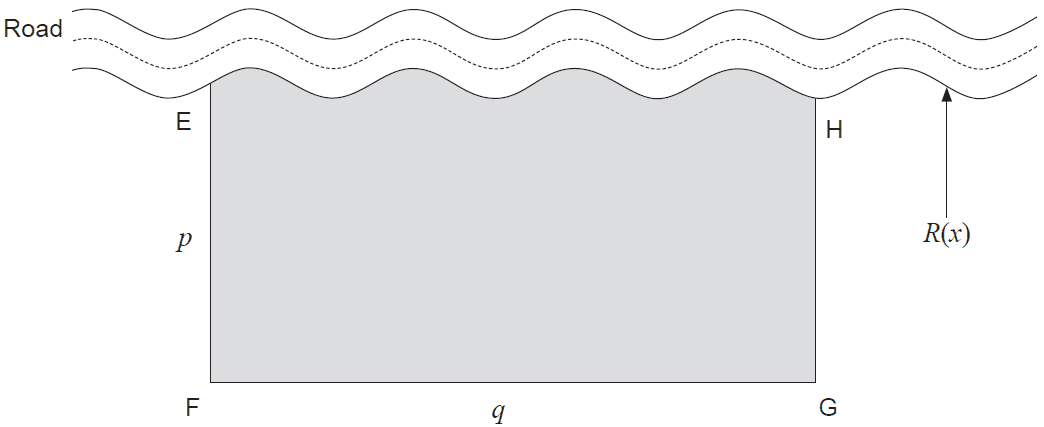
The enclosure is shown as the shaded area above and has right angles at points F and G. David and Katrina want the combined lengths of the fencing from E to F and F to G to equal 500 metres. Let the length of fence EF be equal to \(p\) metres and the length of fence FG be equal to \(q\) metres. If we locate the origin at point F and the x-axis along the line FG, the equation defining the fence along the road is given by:

\[ R(x) = 10 \sin\left(\frac{x}{15}\right) + p \]

(a) Show that the equation defining the area of the enclosure, \(A(q)\), can be given in terms of \(q\) as follows:

\[ A(q) = 500q - 150 \cos\left(\frac{q}{15}\right) - q^2 + 150 \] (4 marks)

(b) Determine, to the nearest metre, the value of \(q\) that will allow the sheep to graze over the maximum area and state this maximum area. (4 marks)

The length of the fence from E to H is given by the equation:

\[ L_{EH} = \int_0^q \sqrt{1 + (R'(x))^2} \, dx \text{, where } R'(x) \text{ is the first derivative of } R(x). \]

(c)

(i) Determine \(R'(x)\). (1 mark)

(ii) Hence determine the total length of fencing required by David and Katrina to enclose their sheep with maximum area for grazing. (3 marks)