WACE Maths Methods ATAR Section 2 Topic Tests
Differential Calculus Topic Test 1
Section Two: Technology-active
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
John is given a prescription for blood pressure tablets by his doctor. Each tablet contains five milligrams of the active medication. The mass of active medication, \(A\), remaining in John's body \(t\) hours after taking a single tablet is given by \[ A(t) = 5e^{-0.0173t} \] where \(A\) is in milligrams.
(a) Calculate the mass of medication remaining in John's body 10 hours after taking a single tablet. (1 mark)
(b) After how many hours will the mass of medication remaining in John's body have halved? (2 marks)
(c) Determine at what rate the mass of medication remaining in John's body is decreasing 24 hours after taking a single tablet. (3 marks)
If a tablet is taken every \(T\) hours, the mass of medication, \(B\), remaining in John's body immediately after taking a tablet will be given by \[ B(T) = \frac{5}{1 - e^{-0.0173T}} \] where \(B\) is in milligrams.
(d) How frequently should John take a tablet so that the mass of medication remaining in his body immediately after taking each tablet is 8.85 mg? (2 marks)
(e) Use the increments formula to approximate the change in \(B\) if the time between taking tablets increased by 30 minutes from the time determined in part (d). (3 marks)
End of questions
Differential Calculus Topic Test 2
Section Two: Technology-active
Number of marks: 12
Reading time: 1 minute
Writing time: 12 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
An analyst was hired by a large company at the beginning of 2021 to develop a model to predict profit. At that time, the company's profit was $4 million. The model developed by the analyst was:
\[ P(x) = \frac{20\ln(x+a)}{x+5}, \]
where \(P(x)\) is the profit in millions of dollars after \(x\) weeks and \(a\) is a constant.
(a) Show that \(a = e\). (2 marks)
(b) What does the model predict the profit will be after five weeks? (1 mark)
(c) Showing use of the quotient rule, determine an equation that, when solved, will give the time when the model predicts the profit will be maximised. (3 marks)
(d) What is this maximum profit and during which week will it occur? (2 marks)
(e) According to the model, during which week will the company's profit fall below its value at the beginning of 2021? (1 mark)
The model proved accurate and after 10 weeks the company implemented some changes. From this time the analyst used a new model to predict the profit:
\[ N(y) = 2e^{b(10+y)}, \]where \(N(y)\) is the profit in millions of dollars \(y\) weeks from this point in time and \(b\) is a constant.
(f) The company is projecting its profit to exceed $5 million. During which week does the new model suggest this will happen? (3 marks)
End of questions
Differential Calculus Topic Test 3
Section Two: Technology-active
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Let \(f(x) = x^2e^x\).
(a) Show that \( f'(x) = xe^x(x+2) \). (2 marks)
(b) Use calculus to determine all the stationary points of \(f(x)\) and determine their nature. (7 marks)
(c) Determine the coordinates of any points of inflection. (2 marks)
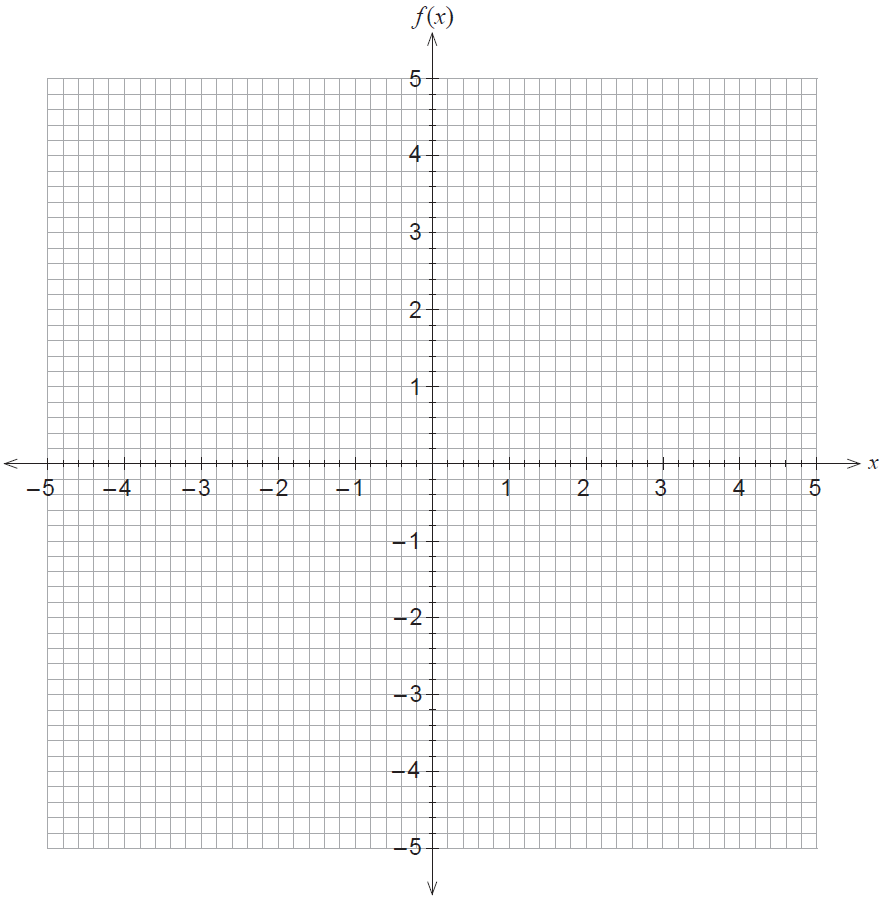
(d) Hence sketch the graph of \(f(x)\), clearly indicating the location of all stationary points and points of inflection. (4 marks)
End of questions
Differential Calculus Topic Test 4
Section Two: Technology-active
Number of marks: 14
Reading time: 1 minute
Writing time: 14 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A beverage company has decided to release a new product. 'Joosilicious' is to be sold in 375 mL cans that are perfectly cylindrical. {Hint: 1 mL = 1 cm³}
(a) If the cans have a base radius of \(x\) cm show that the surface area of the can, \(S\), is given by: \( S = 2\pi x^2 + \frac{750}{x} \). (2 marks)
(b) Using calculus methods, and showing full reasoning and justification, find the dimensions of the can that will minimise its surface area. (4 marks)
Use the quotient rule to show that \( \frac{d}{dx} \tan(x) = \frac{1}{\cos^2(x)} \).
The population of mosquitos, \(P\) (in thousands), in an artificial lake in a housing estate is measured at the beginning of the year. The population after \(t\) months is given by the function, \(P(t) = t^3 + at^2 + bt + 2, 0 \le t \le 12\).
The rate of growth of the population is initially increasing. It then slows to be momentarily stationary in mid-winter (at \(t=6\)), then continues to increase again in the last half of the year.
Determine the values of \(a\) and \(b\).
End of questions
Differential Calculus Topic Test 5
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A group of biologists has decided that colonies of a native Australian animal are in danger if their populations are less than 1000. One such colony had a population of 2300 at the start of 2011. The population was growing continuously such that \(P = P_0 e^{0.065t}\) where \(P\) is the number of animals in the colony \(t\) years after the start of 2011.
(a) Determine, to the nearest 10 animals, the population of the colony at the start of 2014. (2 marks)
(b) Determine the rate of change of the colony's population when \(t = 2.5\) years. (2 marks)
(c) At the beginning of 2017, a disease caused the colony's population to decrease continuously at the rate of 8.25% of the population per year. If this rate continues, when will the colony become 'in danger'? Give your answer to the nearest month. (4 marks)
End of questions
Differential Calculus Topic Test 6
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The concentration, \(C\), of a drug in the blood of a patient \(t\) hours after the initial dose can be modelled by the equation below.
\[ C = 4e^{-0.05t} \text{ mg/L} \]
Patients requiring this drug are said to be in crisis if the concentration of the drug in their blood falls below 2.5 mg/L.
A patient is given a dose of the drug at 9 am.
(a) What was the concentration in the patient's blood immediately following the initial dose? (1 mark)
(b) What is the concentration of the drug in the patient's blood at 11.30 am? (2 marks)
(c) Find the rate of change of \(C\) at 1 pm. (2 marks)
(d) What is the latest time the patient can receive another dose of the drug if they are to avoid being in crisis? (3 marks)
End of questions
Differential Calculus Topic Test 7
Section Two: Technology-active
Number of marks: 12
Reading time: 1 minute
Writing time: 12 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A global financial institution transfers a large aggregate data file every evening from offices around the world to its Hong Kong head office. Once the file is received it must be processed in the company's data warehouse. The time \(T\) required to process a file is normally distributed with a mean of 90 minutes and a standard deviation of 15 minutes.
(a) An evening is selected at random. What is the probability that it takes more than two hours to process the file? (2 marks)
(b) What is the probability that the process takes more than two hours on two out of five days in a week? (3 marks)
The company is considering outsourcing the processing of the files.
(c)
(i) A quotation for this job from an IT company is given in the table below. Complete the table. (1 mark)
| Job duration (minutes) | \(T \le 60\) | \(60 < T < 120\) | \(T \ge 120\) |
|---|---|---|---|
| Probability | |||
| Cost \(Y\) ($) | 200 | 600 | 1200 |
(ii) What is the mean cost? (2 marks)
(iii) Calculate the standard deviation of the cost. (2 marks)
(iv) In the following year, the cost (currently \(\$Y\)) will increase due to inflation and also the introduction of an additional fixed cost, so the new cost \(\$N\) is given by: \(N=aY+b\). In terms of \(a\) and/or \(b\), state the mean cost in the following year and the standard deviation of the cost in the following year. (2 marks)
End of questions
Differential Calculus Topic Test 8
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A group of biologists has decided that colonies of a native Australian animal are in danger if their populations are less than 1000. One such colony had a population of 2300 at the start of 2011. The population was growing continuously such that \(P = P_0 e^{0.065t}\) where \(P\) is the number of animals in the colony \(t\) years after the start of 2011.
(a) Determine, to the nearest 10 animals, the population of the colony at the start of 2014. (2 marks)
(b) Determine the rate of change of the colony's population when \(t = 2.5\) years. (2 marks)
(c) At the beginning of 2017, a disease caused the colony's population to decrease continuously at the rate of 8.25% of the population per year. If this rate continues, when will the colony become 'in danger'? Give your answer to the nearest month. (4 marks)
End of questions
Differential Calculus Topic Test 9
Section Two: Technology-active
Number of marks: 9
Reading time: 1 minute
Writing time: 9 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Let \(f(x) = x \ln(x+3)\).
(a) Use calculus to locate and classify all the stationary points of \(f(x)\) and find any points of inflection. (5 marks)
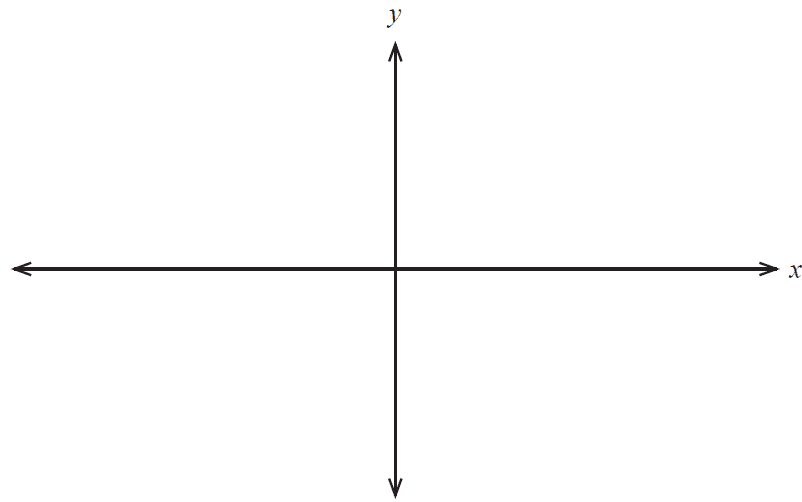
(b) On the axes provided sketch the graph of \(f(x)\), labelling all key features. (4 marks)
End of questions
Differential Calculus Topic Test 10
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A resort in the Swiss Alps features a cable car that travels from the resort station to the mountain station. Engineers are fixing a cable car that unexpectedly stopped shortly before it reached the mountain station. The engineers are ready to test the cable car. For the purposes of the test, the cable car will initially be at rest in its current position, will head up the mountain, stop at the mountain station and immediately return to the resort station where it will stop, and the test will be complete.
The test begins and engineers believe that the acceleration, \(a(t)\), of the cable car during the test will be: \( a(t) = kt^2 - 23t + 20k \), measured in m/min². The variable \(t\) is the number of minutes from the moment the cable car leaves its position and \(k\) is a constant. After two minutes, the engineers expect that the cable car will be travelling with velocity 18 m/min and will not yet have reached the mountain station.
(a) Determine the value of the constant \(k\). (3 marks)
(b) Once the cable car leaves the mountain station, how long should it take to return to the resort station? (3 marks)
(c) Unfortunately, 10 minutes into the test, the cable car breaks down again. According to the engineers' model, how far is the cable car from the mountain station at this time? (2 marks)
End of questions
Differential Calculus Topic Test 11
Section Two: Technology-active
Number of marks: 9
Reading time: 1 minute
Writing time: 9 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A log with a circular cross-section is being prepared for milling. The log is to be cut into five usable pieces, one large beam with a square cross-section and four sideboards, as shown in the diagram below.
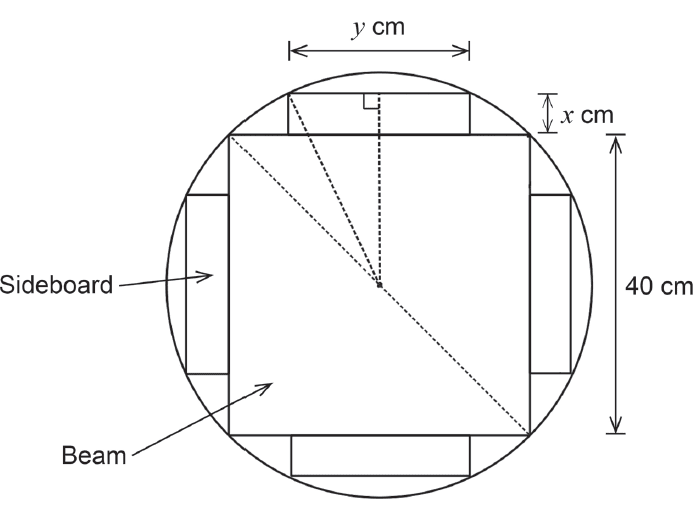
(a) Determine the exact radius of the log. (2 marks)
(b) Using the variables defined in the diagram, show that the cross-sectional area, in cm², of a single sideboard is \(A(x) = 2x \sqrt{400 - 40x - x^2}\). (3 marks)
(c) Use calculus techniques to determine the dimensions \(x\) and \(y\) that maximise the cross-sectional area of one sideboard. (4 marks)
End of questions
Differential Calculus Topic Test 12
Section Two: Technology-active
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A beekeeper is starting a new colony of bees. The population \(B\) of bees, in thousands, is given by \[ B(t) = 4e^{1.4t} \] where \(t\) is the number of years since the establishment of the colony.
(a) Determine the initial population of the bee colony. (1 mark)
(b) Determine the increase in the population of the bee colony in the first six months. (2 marks)
(c) Determine the rate of population growth two years after the establishment of the colony. (2 marks)
(d) After how many years will the rate of population growth be 65 000 bees/year? (2 marks)
After three years, the beekeeper notices that the number of bees begins to decline. The declining population, \(b\), in thousands, has the form \(b(t) = Ae^{rt}\) where \(t\) is the number of years since the start of the decline.
(e) Determine \(A\) and \(r\) if one year after the start of the decline the bee population is 100 000. (4 marks)
End of questions
Differential Calculus Topic Test 13
Section Two: Technology-active
Number of marks: 8
Reading time: 1 minute
Writing time: 8 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The Interesting Architecture company has designed a building with a constant cross-section shown in the figure below.
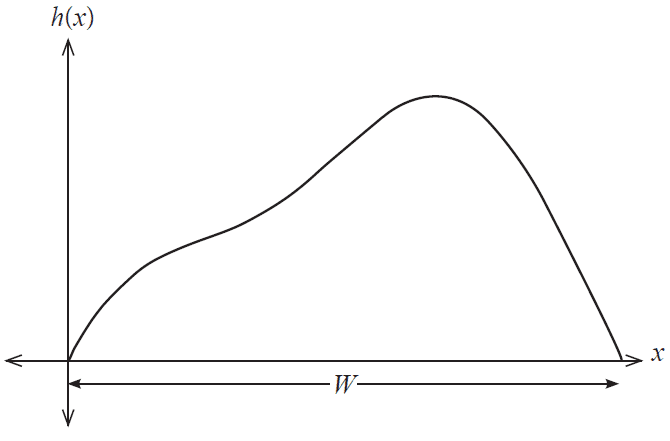
With reference to the figure, the height \(h(x)\) of the building at a point \(x\) along its width is given by
\[ h(x) = 4\sin\left(x - \frac{3\pi}{2}\right) - x^2 + 3\pi x - 4, \text{ where } h \text{ and } 0 \le x \le W \text{ are measured in metres.} \]
(a) Determine the width \(W\) of the building to the nearest centimetre. (2 marks)
(b) Determine \(h'(x)\). (1 mark)
(c) Determine, to the nearest centimetre, the value of \(x\) at which the height of the building is maximum and state this maximum height. (2 marks)
(d) An adventure company allows tourists to climb from the ground on the left of the building, then along the outside of the building to the top. The company installs a platform that allows climbers to rest on their way up to the top. The platform is located on the second half of the climb, at the point where it is the steepest. How high off the ground, to the nearest centimetre, is it positioned? (3 marks)
End of questions
Differential Calculus Topic Test 14
Section Two: Technology-active
Number of marks: 7
Reading time: 1 minute
Writing time: 7 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Water flows into a bowl at a constant rate. The water level, \(h\), measured in centimetres, increases at a rate given by
\[ h'(t) = \frac{4t+1}{2t^2+t+1} \]
where the time \(t\) is measured in seconds.
(a) Determine the rate that the water level is rising when \(t=2\) seconds. (1 mark)
(b) Explain why \(h(t) = \ln(2t^2+t+1) + c\). (2 marks)
(c) Determine the total change in the water level over the first 2 seconds. (1 mark)
The bowl is filled when the water level reaches \(\ln(56)\) cm.
(d) If the bowl is initially empty, determine how long it takes for the bowl to be filled. (3 marks)
End of questions
Differential Calculus Topic Test 15
Section Two: Technology-active
Number of marks: 9
Reading time: 1 minute
Writing time: 9 minutes
Section Two:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
A chef needs to use an oven to boil 100 mL of water in five minutes for a new experimental recipe. The temperature of the water must reach 100 °C in order to boil. The temperature, \(T\), of 100 mL of water \(t\) minutes after being placed in an oven set to \(T_0\) °C can be modelled by the equation below.
\[ T(t) = T_0 - 175e^{-0.07t} \]
In a preliminary experiment, the chef placed a 100 mL bowl of water into an oven that had been heated to \(T_0 = 200\) °C.
(a) What is the temperature of the water at the moment it is placed into the oven? (1 mark)
(b) What is the temperature of the water five minutes after being placed in the oven? (1 mark)
(c) What change could be made to the temperature at which the oven is set in order to achieve the five-minute boiling requirement? (2 marks)
Assume that \(T_0\) is still 200 °C.
(d) Determine the rate of increase in temperature of the water five minutes after being placed in the oven. Give your answer rounded to two decimal places. (2 marks)
(e) Explain what happens to the rate of change in the temperature of the water as time increases and how this relates to the temperature of the water. (3 marks)
End of questions



