VCE Methods Probability Application Task 2

Question 1 [2020 Exam 2 Section B Q3]

A transport company has detailed records of all its deliveries. The number of minutes a delivery is made before or after its scheduled delivery time can be modelled as a normally distributed random variable, \(T\), with a mean of zero and a standard deviation of four minutes. A graph of the probability distribution of \(T\) is shown below.

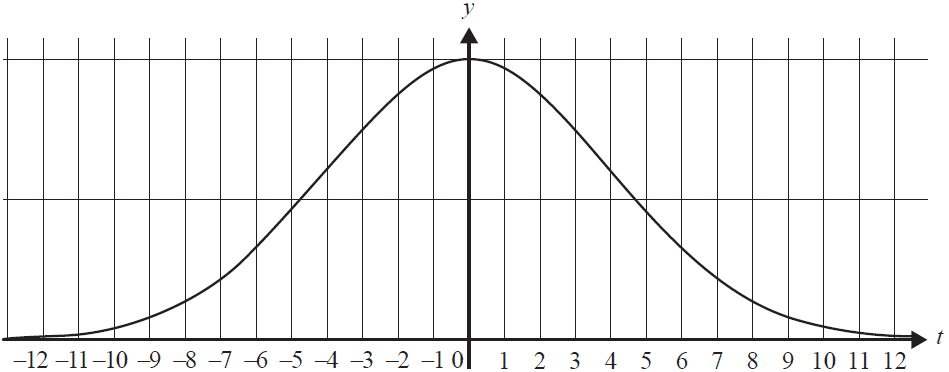
a. If \(\Pr(T \le a) = 0.6\), find \(a\) to the nearest minute. 1 mark

b. Find the probability, correct to three decimal places, of a delivery being no later than three minutes after its scheduled delivery time, given that it arrives after its scheduled delivery time. 2 marks

c. Using the model described on page 19, the transport company can make 46.48% of its deliveries over the interval \(-3 \le t \le 2\).
It has an improved delivery model with a mean of \(k\) and a standard deviation of four minutes.
Find the values of \(k\), correct to one decimal place, so that 46.48% of the transport company’s deliveries can be made over the interval \(-4.5 \le t \le 0.5\). 3 marks

A rival transport company claims that there is a 0.85 probability that each delivery it makes will arrive on time or earlier.
Assume that whether each delivery is on time or earlier is independent of other deliveries.

d. Assuming that the rival company’s claim is true, find the probability that on a day in which the rival company makes eight deliveries, fewer than half of them arrive on time or earlier. Give your answer correct to three decimal places. 2 marks

e. Assuming that the rival company’s claim is true, consider a day in which it makes \(n\) deliveries.

i. Express, in terms of \(n\), the probability that one or more deliveries will not arrive on time or earlier. 1 mark

ii. Hence, or otherwise, find the minimum value of \(n\) such that there is at least a 0.95 probability that one or more deliveries will not arrive on time or earlier. 1 mark

f. An analyst from a government department believes the rival transport company’s claim is only true for deliveries made before 4 pm. For deliveries made after 4 pm, the analyst believes the probability of a delivery arriving on time or earlier is \(x\), where \(0.3 \le x \le 0.7\).
After observing a large number of the rival transport company’s deliveries, the analyst believes that the overall probability that a delivery arrives on time or earlier is actually 0.75.
Let the probability that a delivery is made after 4 pm be \(y\).
Assuming that the analyst’s beliefs are true, find the minimum and maximum values of \(y\). 2 marks