VCE Methods Probability Application Task 1
Number of marks: 19
Reading time: 3 minutes
Writing time: 28 minutes
Section B – Calculator Allowed
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The time Jennifer spends on her homework each day varies, but she does some homework every day.
The continuous random variable \(T\), which models the time, \(t\), in minutes, that Jennifer spends each day on her homework, has a probability density function \(f\), where
\( f(t) = \begin{cases} \frac{1}{625}(t-20) & 20 \le t < 45 \\ \frac{1}{625}(70-t) & 45 \le t \le 70 \\ 0 & \text{elsewhere} \end{cases} \)
a. Sketch the graph of \(f\) on the axes provided below. 3 marks
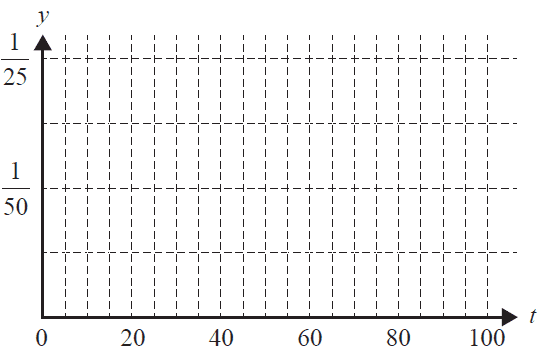
b. Find \(\Pr(25 \le T \le 55)\). 2 marks
c. Find \(\Pr(T \le 25 | T \le 55)\). 2 marks
d. Find \(a\) such that \(\Pr(T > a) = 0.7\), correct to four decimal places. 2 marks
e. The probability that Jennifer spends more than 50 minutes on her homework on any given day is \(\frac{8}{25}\). Assume that the amount of time spent on her homework on any day is independent of the time spent on her homework on any other day.
i. Find the probability that Jennifer spends more than 50 minutes on her homework on more than three of seven randomly chosen days, correct to four decimal places. 2 marks
ii. Find the probability that Jennifer spends more than 50 minutes on her homework on at least two of seven randomly chosen days, given that she spends more than 50 minutes on her homework on at least one of those days, correct to four decimal places. 2 marks
f. Let \(p\) be the probability that on any given day Jennifer spends more than \(d\) minutes on her homework.
Let \(q\) be the probability that on two or three days out of seven randomly chosen days she spends more than \(d\) minutes on her homework.
Express \(q\) as a polynomial in terms of \(p\). 2 marks
g.
i. Find the maximum value of \(q\), correct to four decimal places, and the value of \(p\) for which this maximum occurs, correct to four decimal places. 2 marks
ii. Find the value of \(d\) for which the maximum found in part g.i. occurs, correct to the nearest minute. 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

