VCE Methods Integral Calculus Application Task 3

Question 1 [2023 Exam 2 Section B Q2]

The following diagram represents an observation wheel, with its centre at point P. Passengers are seated in pods, which are carried around as the wheel turns. The wheel moves anticlockwise with constant speed and completes one full rotation every 30 minutes. When a pod is at the lowest point of the wheel (point A), it is 15 metres above the ground. The wheel has a radius of 60 metres.

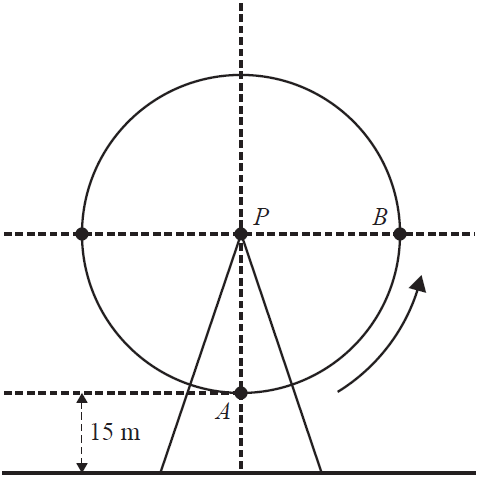
Consider the function \( h(t) = -60 \cos(bt) + c \) for some \( b, c \in \mathbb{R} \), which models the height above the ground of a pod originally situated at point A, after time \( t \) minutes.

a. Show that \( b = \frac{\pi}{15} \) and \( c = 75 \). 2 marks

b. Find the average height of a pod on the wheel as it travels from point A to point B. Give your answer in metres, correct to two decimal places. 2 marks

c. Find the average rate of change, in metres per minute, of the height of a pod on the wheel as it travels from point A to point B. 1 mark

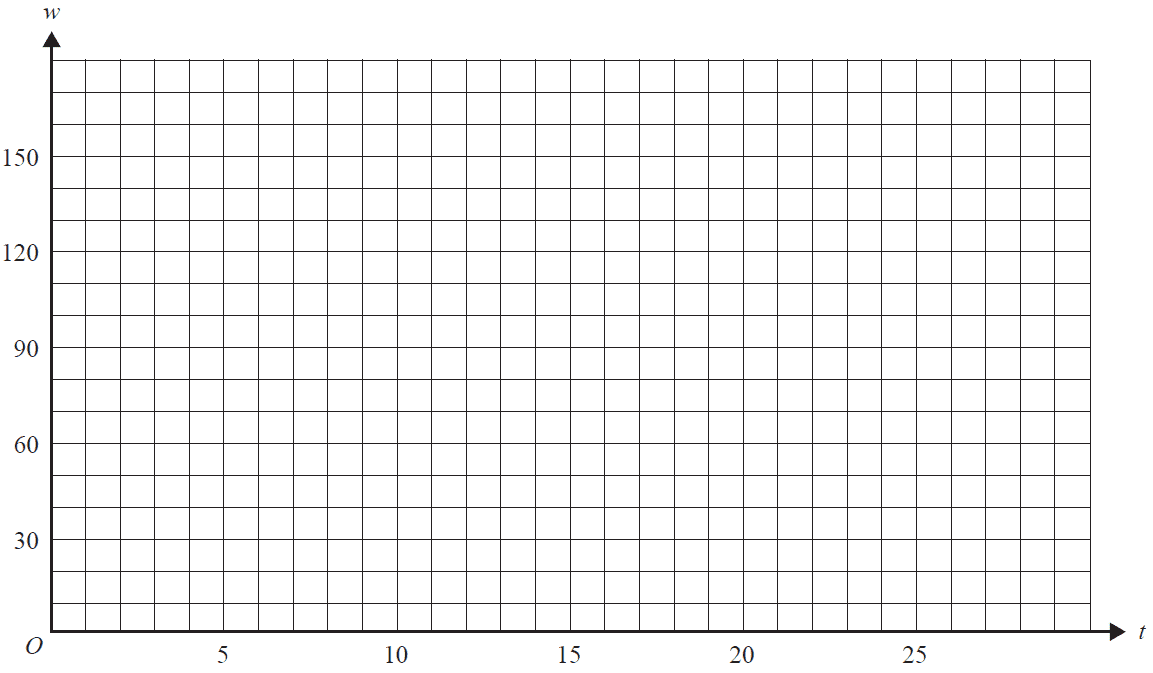
After 15 minutes, the wheel stops moving and remains stationary for 5 minutes. After this, it continues moving at double its previous speed for another 7.5 minutes. The height above the ground of a pod that was initially at point A, after \( t \) minutes, can be modelled by the piecewise function \( w \):

\[ w(t) = \begin{cases} h(t) & 0 \leq t < 15 \\ k & 15 \leq t < 20 \\ h(mt + n) & 20 \leq t \leq 27.5 \end{cases} \] where \( k \geq 0 \), \( m \geq 0 \) and \( n \in \mathbb{R} \).

d. i. State the values of \( k \) and \( m \). 1 mark

ii. Find all possible values of \( n \). 2 marks

iii. Sketch the graph of the piecewise function \( w \) on the axes below, showing the coordinates of the endpoints. 3 marks