2024 VCE Maths Methods Mini Test 5
Number of marks: 14
Reading time: 2 minutes
Writing time: 20 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
At a Year 12 formal, 45% of the students travelled to the event in a hired limousine, while the remaining 55% were driven by a parent.
Of the students who travelled in a hired limousine, 30% had a professional photo taken.
Of the students who were driven by a parent, 60% had a professional photo taken.
Given that a student had a professional photo taken, what is the probability that the student travelled in a hired limousine?
- A. \(\frac{1}{8}\)
- B. \(\frac{27}{200}\)
- C. \(\frac{9}{31}\)
- D. \(\frac{22}{31}\)
Suppose a function \( f: [0, 5] \to \mathbb{R} \) and its derivative \( f': [0, 5] \to \mathbb{R} \) are defined and continuous on their domains.
If \( f'(2) < 0 \) and \( f'(4) > 0 \), which one of these statements must be true?
- A. f is strictly decreasing on [0, 2]
- B. f does not have an inverse function
- C. f is positive on [4, 5]
- D. f has a local minimum at x = 3
Twelve students sit in a classroom, with seven students in the first row and five in the second row. Three students are chosen randomly from the class.
The probability that exactly two of the three students chosen are in the first row is
- A. \(\frac{7}{44}\)
- B. \(\frac{21}{44}\)
- C. \(\frac{5}{22}\)
- D. \(\frac{245}{576}\)
The graph of \( y = f(x) \) is shown below
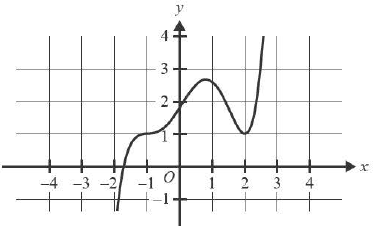
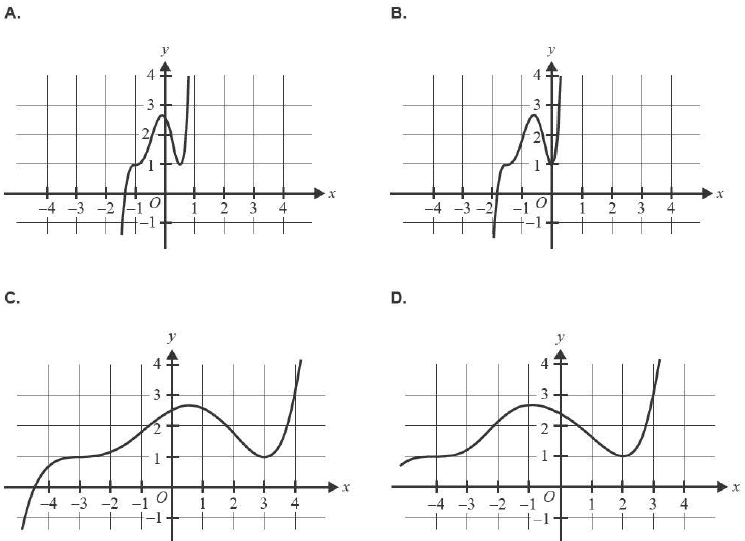
Which of the following options best represents the graph of \( y = f(2x + 1) \)?
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The function \( h : [0, \infty) \rightarrow \mathbb{R},\ h(t) = \frac{3000}{t + 1} \) models the population of a town after \( t \) years.
a. Use the model \( h(t) \) to predict the population of the town after four years. 1 mark
b. A new function, \( h_1 \), models a population where \( h_1(0) = h(0) \) but \( h_1 \) decreases at half the rate of \( h \) at any point in time.
State a sequence of two transformations that maps \( h \) to this new model \( h_1 \). 2 marks
c. In the town, 100 people were randomly selected and surveyed, with 60 people indicating that they were unhappy with the roads.
i. Determine an approximate 95% confidence interval for the proportion of people in the town who are unhappy with the roads. Use \( z = 2 \) for this confidence interval. 2 marks
ii. A new sample of \( n \) people results in the same sample proportion.
Find the smallest value of \( n \) to achieve a standard deviation of \( \frac{\sqrt{2}}{50} \) for the sample proportion. 1 mark
Solve \( 2\log_3(x - 4) + \log_3(x) = 2 \) for \( x \). 4 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

