2024 VCE Maths Methods Mini Test 7
Number of marks: 13
Reading time: 2 minutes
Writing time: 18 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The function \( f: (0, \infty) \to \mathbb{R}, f(x) = \frac{x}{2}+\frac{2}{x} \) is mapped to a function \( g \) by:
1. dilation by a factor of 3 from the y-axis
2. translation by 1 unit in the negative y-direction
The function \( g \) has a local minimum at
- A. (6, 1)
- B. \((\frac{2}{3}, 1)\)
- C. (2, 5)
- D. \((2, -\frac{1}{3})\)
Let \( h \) be the probability density function for a continuous random variable \( X \), where
\[ h(x) = \begin{cases} \dfrac{x}{6} + k, & \text{for } -3 \leq x < 0 \\ -\dfrac{x}{2} + k, & \text{for } 0 \leq x \leq 1 \\ 0, & \text{elsewhere} \end{cases} \]
and \( k \) is a positive real number.
The value of \( \Pr(X < 0.5) \) is
- A. \(\frac{1}{2}\)
- B. \(\frac{15}{16}\)
- C. \(\frac{3}{16}\)
- D. \(\frac{49}{48}\)
The points of inflection of the graph of \( y = 2 - \tan(\pi(x - \tfrac{1}{4})) \) are
- A. \((k + \tfrac{1}{4}, 2), k \in \mathbb{Z}\)
- B. \((k - \tfrac{1}{4}, 2), k \in \mathbb{Z}\)
- C. \((k + \tfrac{1}{4}, -2), k \in \mathbb{Z}\)
- D. \((k - \tfrac{3}{4}, -2), k \in \mathbb{Z}\)
Suppose that a differentiable function \( f: \mathbb{R} \to \mathbb{R} \) and its derivative \( f' : \mathbb{R} \to \mathbb{R} \) satisfy \( f(4) = 25 \) and \( f'(4) = 15 \).
Determine the gradient of the tangent line to the graph of \( y = \sqrt{f(x)} \) at \( x = 4 \).
- A. \(\sqrt{15}\)
- B. \(\frac{1}{10}\)
- C. \(\frac{15}{2}\)
- D. \(\frac{3}{2}\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Part of the graph of \( f : [-\pi, \pi] \rightarrow \mathbb{R},\ f(x) = x\sin(x) \) is shown below.
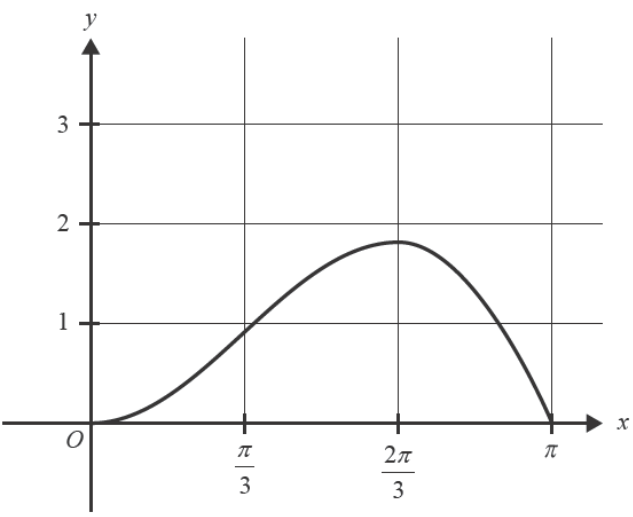
a. Use the trapezium rule with a step size of \( \frac{\pi}{3} \) to determine an approximation of the total area between the graph of \( y = f(x) \) and the x-axis over the interval \( x \in [0, \pi] \). 3 marks
b.
i. Find \( f'(x) \). 1 mark
ii. Determine the range of \( f'(x) \) over the interval \( \left[\frac{\pi}{3}, \frac{2\pi}{3} \right] \). 1 mark
iii. Hence, verify that \( f(x) \) has a stationary point for \( x \in \left[\frac{\pi}{3}, \frac{2\pi}{3} \right] \). 1 mark
c. On the set of axes below, sketch the graph of \( y = f'(x) \) on the domain \( [-\pi, \pi] \), labelling the endpoints with their coordinates.
You may use the fact that the graph of \( y = f'(x) \) has a local minimum at approximately \( (-1.1, -1.4) \) and a local maximum at approximately \( (1.1, 1.4) \). 3 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

