2022 VCE Maths Methods Mini Test 4
Number of marks: 12
Reading time: 2 minutes
Writing time: 18 minutes
Section B – Calculator Allowed
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
On a remote island, there are only two species of animals: foxes and rabbits. The foxes are the predators and the rabbits are their prey.
The populations of foxes and rabbits increase and decrease in a periodic pattern, with the period of both populations being the same, as shown in the graph below, for all \( t \geq 0 \), where time \( t \) is measured in weeks.
One point of minimum fox population, \( (20, 700) \), and one point of maximum fox population, \( (100, 2500) \), are also shown on the graph.
The graph has been drawn to scale.
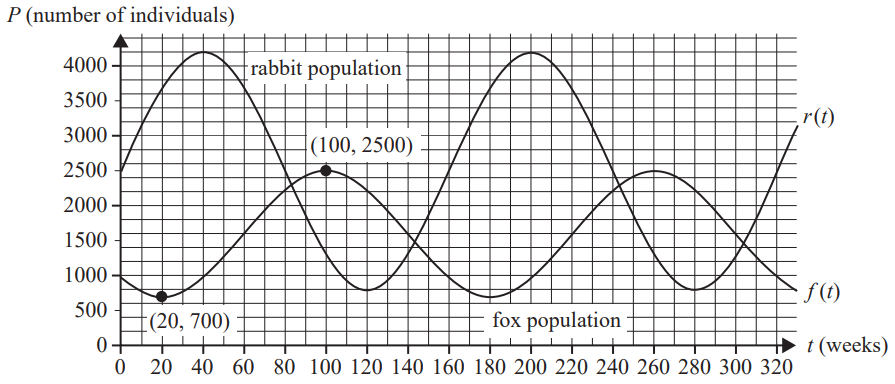
a. i. State the initial population of rabbits. 1 mark
ii. State the minimum and maximum population of rabbits. 1 mark
iii. State the number of weeks between maximum populations of rabbits. 1 mark
The population of foxes can be modelled by the rule \( f(t) = a \sin\big(b(t - 60)\big) + 1600 \).
b. Show that \( a = 900 \) and \( b = \frac{\pi}{80} \). 2 marks
c. Find the maximum combined population of foxes and rabbits. Give your answer correct to the nearest whole number. 1 mark
d. What is the number of weeks between the periods when the combined population of foxes and rabbits is a maximum? 1 mark
e. This question is no longer in the curriculum
Over a longer period of time, it is found that the increase and decrease in the population of rabbits gets smaller and smaller.
The population of rabbits over a longer period of time can be modelled by the rule
\( s(t) = 1700 \cdot e^{-0.003t} \cdot \sin\left( \frac{\pi t}{80} \right) + 2500, \quad \text{for all } t \geq 0 \)
f. Find the average rate of change between the first two times when the population of rabbits is at a maximum. Give your answer correct to one decimal place. 2 marks
g. Find the time, where \( t > 40 \), in weeks, when the rate of change of the rabbit population is at its greatest positive value. Give your answer correct to the nearest whole number. 2 marks
h. Over time, the rabbit population approaches a particular value.
State this value. 1 mark
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

