VCE General Maths Recursion and Financial Modelling 2020 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Recursion and financial modelling - 2020 (Part 1)
The following recurrence relation can generate a sequence of numbers.
\(T_0 = 10, \quad T_{n+1} = T_n + 3\)
The number 13 appears in this sequence as
- A. \(T_1\)
- B. \(T_2\)
- C. \(T_3\)
- D. \(T_{10}\)
- E. \(T_{13}\)
An asset is purchased for $2480.
The value of this asset after \(n\) time periods, \(V_n\), can be determined using the rule
\(V_n = 2480 + 45n\)
A recurrence relation that also models the value of this asset after \(n\) time periods is
- A. \(V_0 = 2480, \quad V_{n+1} = V_n + 45n\)
- B. \(V_1 = 2480, \quad V_{n+1} = V_n + 45n\)
- C. \(V_0 = 2480, \quad V_{n+1} = V_n + 45\)
- D. \(V_1 = 2480, \quad V_{n+1} = V_n + 45\)
- E. \(V_n = 2480, \quad V_{n+1} = V_n + 45\)
Consider the following four recurrence relations representing the value of an asset after \(n\) years, \(V_n\).
- \(V_0 = 20000, \quad V_{n+1} = V_n + 2500\)
- \(V_0 = 20000, \quad V_{n+1} = V_n - 2500\)
- \(V_0 = 20000, \quad V_{n+1} = 0.875V_n\)
- \(V_0 = 20000, \quad V_{n+1} = 1.125V_n - 2500\)
How many of these recurrence relations indicate that the value of an asset is depreciating?
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
Manu invests $3000 in an account that pays interest compounding monthly. The balance of his investment after \(n\) months, \(B_n\), can be determined using the recurrence relation
\(B_0 = 3000, \quad B_{n+1} = 1.0048 \times B_n\)
The total interest earned by Manu's investment after the first five months is closest to
- A. $57.60
- B. $58.02
- C. $72.00
- D. $72.69
- E. $87.44
The graph below represents the value of an annuity investment, \(A_n\), in dollars, after \(n\) time periods.
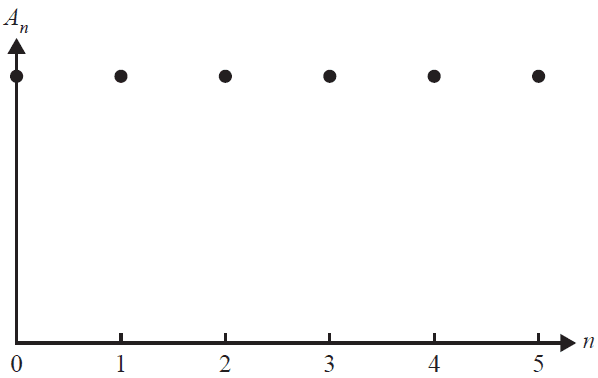
A recurrence relation that could match this graphical representation is
- A. \(A_0 = 200\,000, \quad A_{n+1} = 1.015A_n - 2500\)
- B. \(A_0 = 200\,000, \quad A_{n+1} = 1.025A_n - 5000\)
- C. \(A_0 = 200\,000, \quad A_{n+1} = 1.03A_n - 5500\)
- D. \(A_0 = 200\,000, \quad A_{n+1} = 1.04A_n - 6000\)
- E. \(A_0 = 200\,000, \quad A_{n+1} = 1.05A_n - 8000\)
Ray deposited $5000 in an investment account earning interest at the rate of 3% per annum, compounding quarterly.
A rule for the balance, \(R_n\), in dollars, after \(n\) years is given by
- A. \(R_n = 5000 \times 0.03^n\)
- B. \(R_n = 5000 \times 1.03^n\)
- C. \(R_n = 5000 \times 0.03^{4n}\)
- D. \(R_n = 5000 \times 1.0075^n\)
- E. \(R_n = 5000 \times 1.0075^{4n}\)
Gen invests $10 000 at an interest rate of 5.5% per annum, compounding annually.
After how many years will her investment first be more than double its original value?
- A. 12
- B. 13
- C. 14
- D. 15
- E. 16
The nominal interest rate for a loan is 8% per annum.
When rounded to two decimal places, the effective interest rate for this loan is not
- A. 8.33% per annum when interest is charged daily.
- B. 8.32% per annum when interest is charged weekly.
- C. 8.31% per annum when interest is charged fortnightly.
- D. 8.30% per annum when interest is charged monthly.
- E. 8.24% per annum when interest is charged quarterly.
The value of a van purchased for $45 000 is depreciated by \(k\)\% per annum using the reducing balance method.
After three years of this depreciation, it is then depreciated in the fourth year under the unit cost method at the rate of 15 cents per kilometre.
The value of the van after it travels 30 000 km in this fourth year is $26 166.24
The value of \(k\) is
- A. 9
- B. 12
- C. 14
- D. 16
- E. 18
Twenty years ago, Hector invested a sum of money in an account earning interest at the rate of 3.2% per annum, compounding monthly.
After 10 years, he made a one-off extra payment of $10 000 to the account.
For the next 10 years, the account earned interest at the rate of 2.8% per annum, compounding monthly.
The balance of his account today is $686 904.09
The sum of money Hector originally invested is closest to
- A. $355 000
- B. $370 000
- C. $377 000
- D. $384 000
- E. $385 000
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
