VCE General Maths Recursion and Financial Modelling 2018 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Recursion and financial modelling - 2018
Use the following information to answer Questions 17 and 18.
The value of an annuity investment, in dollars, after \(n\) years, \(V_n\), can be modelled by the recurrence relation shown below.
\(V_0 = 46\,000, \quad V_{n+1} = 1.0034 V_n + 500\)
Question 1What is the value of the regular payment added to the principal of this annuity investment?
- A. $34.00
- B. $156.40
- C. $466.00
- D. $500.00
- E. $656.40
Between the second and third years, the increase in the value of this investment is closest to
- A. $656
- B. $658
- C. $661
- D. $1315
- E. $1975
Daniel borrows $5000, which he intends to repay fully in a lump sum after one year.
The annual interest rate and compounding period for five different compound interest loans are given below:
- Loan I – 12.6% per annum, compounding weekly
- Loan II – 12.8% per annum, compounding weekly
- Loan III – 12.9% per annum, compounding weekly
- Loan IV – 12.7% per annum, compounding quarterly
- Loan V – 13.2% per annum, compounding quarterly
When fully repaid, the loan that will cost Daniel the least amount of money is
- A. Loan I.
- B. Loan II.
- C. Loan III.
- D. Loan IV.
- E. Loan V.
The graph below shows the value, \(V_n\), of an asset as it depreciates over a period of five months.
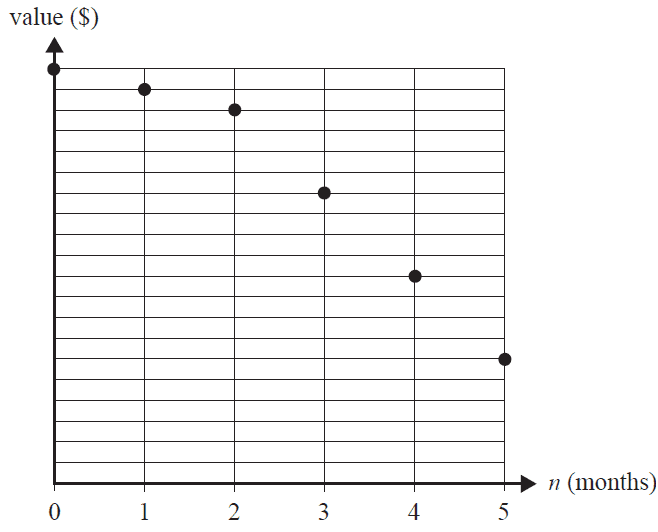
Which one of the following depreciation situations does this graph best represent?
- A. flat rate depreciation with a decrease in depreciation rate after two months
- B. flat rate depreciation with an increase in depreciation rate after two months
- C. unit cost depreciation with a decrease in units used per month after two months
- D. reducing balance depreciation with an increase in the rate of depreciation after two months
- E. reducing balance depreciation with a decrease in the rate of depreciation after two months
Which one of the following recurrence relations could be used to model the value of a perpetuity investment, \(P_n\), after \(n\) months?
- A. \(P_0 = 120\,000, \quad P_{n+1} = 1.0029 \times P_n - 356\)
- B. \(P_0 = 180\,000, \quad P_{n+1} = 1.0047 \times P_n - 846\)
- C. \(P_0 = 210\,000, \quad P_{n+1} = 1.0071 \times P_n - 1534\)
- D. \(P_0 = 240\,000, \quad P_{n+1} = 0.0047 \times P_n - 2232\)
- E. \(P_0 = 250\,000, \quad P_{n+1} = 0.0085 \times P_n - 2125\)
Adam has a home loan with a present value of $175 260.56
The interest rate for Adam’s loan is 3.72% per annum, compounding monthly.
His monthly repayment is $3200.
The loan is to be fully repaid after five years.
Adam knows that the loan cannot be exactly repaid with 60 repayments of $3200.
To solve this problem, Adam will make 59 repayments of $3200. He will then adjust the value of the final repayment so that the loan is fully repaid with the 60th repayment.
The value of the 60th repayment will be closest to
- A. $368.12
- B. $2831.88
- C. $3200.56
- D. $3557.09
- E. $3568.12
Five lines of an amortisation table for a reducing balance loan with monthly repayments are shown below.
| Repayment number | Repayment | Interest | Principal reduction | Balance of loan |
|---|---|---|---|---|
| 25 | $2200.00 | $972.24 | $1227.76 | $230 256.78 |
| 26 | $2200.00 | $967.08 | $1232.92 | $229 023.86 |
| 27 | $2200.00 | $961.90 | $1238.10 | $227 785.76 |
| 28 | $2200.00 | $1002.26 | $1197.74 | $226 588.02 |
| 29 | $2200.00 | $996.99 | $1203.01 | $225 385.01 |
The interest rate for this loan changed immediately before repayment number 28.
This change in interest rate is best described as
- A. an increase of 0.24% per annum.
- B. a decrease of 0.024% per annum.
- C. an increase of 0.024% per annum.
- D. a decrease of 0.0024% per annum.
- E. an increase of 0.00024% per annum.
Mariska plans to retire from work 10 years from now.
Her retirement goal is to have a balance of $600 000 in an annuity investment at that time.
The present value of this annuity investment is $265 298.48, on which she earns interest at the rate of 3.24% per annum, compounding monthly.
To make this investment grow faster, Mariska will add a $1000 payment at the end of every month.
Two years from now, she expects the interest rate of this investment to fall to 3.20% per annum, compounding monthly. It is expected to remain at this rate until Mariska retires.
When the interest rate drops, she must increase her monthly payment if she is to reach her retirement goal.
The value of this new monthly payment will be closest to
- A. $1234
- B. $1250
- C. $1649
- D. $1839
- E. $1854
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
