VCE General Maths Recursion and Financial Modelling 2016 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Recursion and financial modelling - 2016
The value of an annuity, \(V_n\), after \(n\) monthly payments of $555 have been made, can be determined using the recurrence relation
\(V_0 = 100\,000, \quad V_{n+1} = 1.0025 V_n - 555\)
The value of the annuity after five payments have been made is closest to
- A. $97 225
- B. $98 158
- C. $98 467
- D. $98 775
- E. $110 224
The purchase price of a car was $26 000.
Using the reducing balance method, the value of the car is depreciated by 8% each year.
A recurrence relation that can be used to determine the value of the car after \(n\) years, \(C_n\), is
- A. \(C_0 = 26\,000, \quad C_{n+1} = 0.92 C_n\)
- B. \(C_0 = 26\,000, \quad C_{n+1} = 1.08 C_n\)
- C. \(C_0 = 26\,000, \quad C_{n+1} = C_n + 8\)
- D. \(C_0 = 26\,000, \quad C_{n+1} = C_n - 8\)
- E. \(C_0 = 26\,000, \quad C_{n+1} = 0.92 C_n - 8\)
Consider the recurrence relation below.
\(V_0 = 10\,000, \quad V_{n+1} = 1.04 V_n + 500\)
This recurrence relation could be used to model
- A. a reducing balance depreciation of an asset initially valued at $10 000.
- B. a reducing balance loan with periodic repayments of $500.
- C. a perpetuity with periodic payments of $500 from the annuity.
- D. an annuity investment with periodic additions of $500 made to the investment.
- E. an interest-only loan of $10 000.
Juanita invests $80 000 in a perpetuity that will provide $4000 per year to fund a scholarship at a university.
The graph that shows the value of this perpetuity over a period of five years is
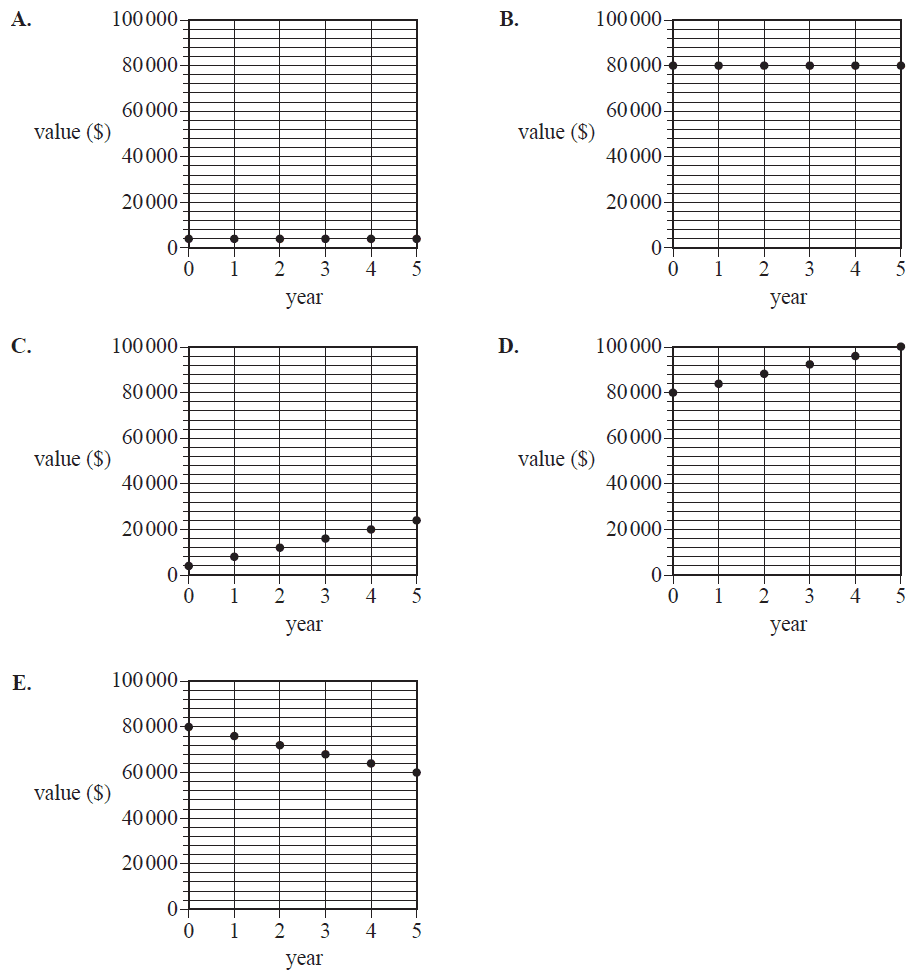
The first three lines of an amortisation table for a reducing balance home loan are shown below.
The interest rate for this home loan is 4.8% per annum compounding monthly.
The loan is to be repaid with monthly payments of $1500.
| Payment number | Payment | Interest | Principal reduction | Balance of loan |
|---|---|---|---|---|
| 0 | 0 | 0.00 | 0.00 | 250 000.00 |
| 1 | 1500 | 1000.00 | 500.00 | 249 500.00 |
| 2 | 1500 |
The amount of payment number 2 that goes towards reducing the principal of the loan is
- A. $486
- B. $502
- C. $504
- D. $996
- E. $998
Sarah invests $5000 in a savings account that pays interest at the rate of 3.9% per annum compounding quarterly. At the end of each quarter, immediately after the interest has been paid, she adds $200 to her investment.
After two years, the value of her investment will be closest to
- A. $5805
- B. $6600
- C. $7004
- D. $7059
- E. $9285
Mai invests in an annuity that earns interest at the rate of 5.2% per annum compounding monthly.
Monthly payments are received from the annuity.
The balance of the annuity will be $130 784.93 after five years.
The balance of the annuity will be $66 992.27 after 10 years.
The monthly payment that Mai receives from the annuity is closest to
- A. $1270
- B. $1400
- C. $1500
- D. $2480
- E. $3460
SECTION B – Modules
Module 1 – Matrices
Question 8The transpose of \(\begin{bmatrix} 2 & 7 & 10 \\ 13 & 19 & 8 \end{bmatrix}\) is
- A. \(\begin{bmatrix} 13 & 19 & 8 \\ 2 & 7 & 10 \end{bmatrix}\)
- B. \(\begin{bmatrix} 10 & 7 & 2 \\ 8 & 19 & 13 \end{bmatrix}\)
- C. \(\begin{bmatrix} 2 & 13 \\ 7 & 19 \\ 10 & 8 \end{bmatrix}\)
- D. \(\begin{bmatrix} 13 & 2 \\ 19 & 7 \\ 8 & 10 \end{bmatrix}\)
- E. \(\begin{bmatrix} 8 & 10 \\ 19 & 7 \\ 13 & 2 \end{bmatrix}\)
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
