VCE General Maths Networks and Decision Mathematics 2023 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Networks and decision mathematics - 2023 - Exam 2)
A country has five states, \(A, B, C, D\) and \(E\).
A graph can be drawn with vertices to represent each of the states.
Edges represent a border shared between two states.
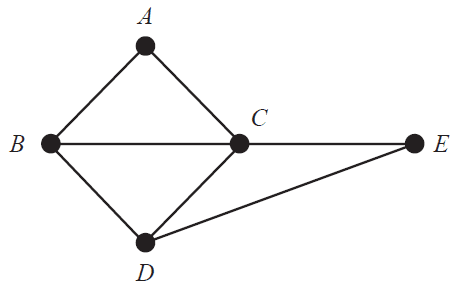
a. What is the sum of the degrees of the vertices of the graph above? 1 mark
b. Euler’s formula, \(v + f = e + 2\), holds for this graph.
i. Complete the formula by writing the appropriate numbers in the boxes provided below. 1 mark

ii. Complete the sentence by writing the appropriate word in the box provided below. 1 mark
Euler’s formula holds for this graph because the graph is connected and .
c. The diagram below shows the position of state \(A\) on a map of this country.
The four other states are indicated on the diagram as 1, 2, 3 and 4.
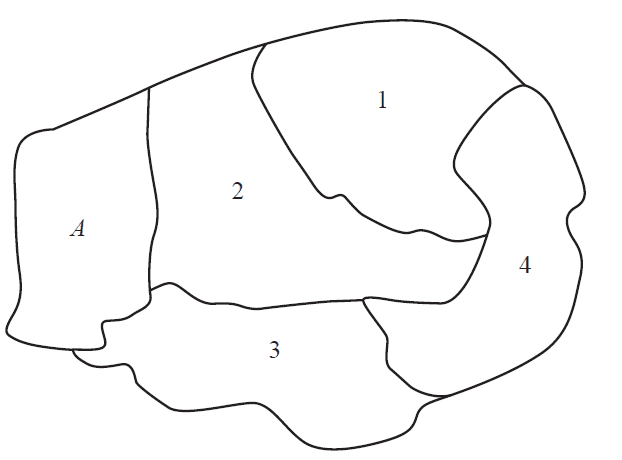
Use the information in the graph on page 20 to complete the table below. Match the state (\(B, C, D\) and \(E\)) with the corresponding state number (1, 2, 3 and 4) given in the map above. 1 mark
| State | State number |
|---|---|
| B | |
| C | |
| D | |
| E |
The state \(A\) has nine landmarks, \(G, H, I, J, K, L, M, N\) and \(O\).
The edges on the graph represent the roads between the landmarks.
The numbers on each edge represent the length, in kilometres, along each road.
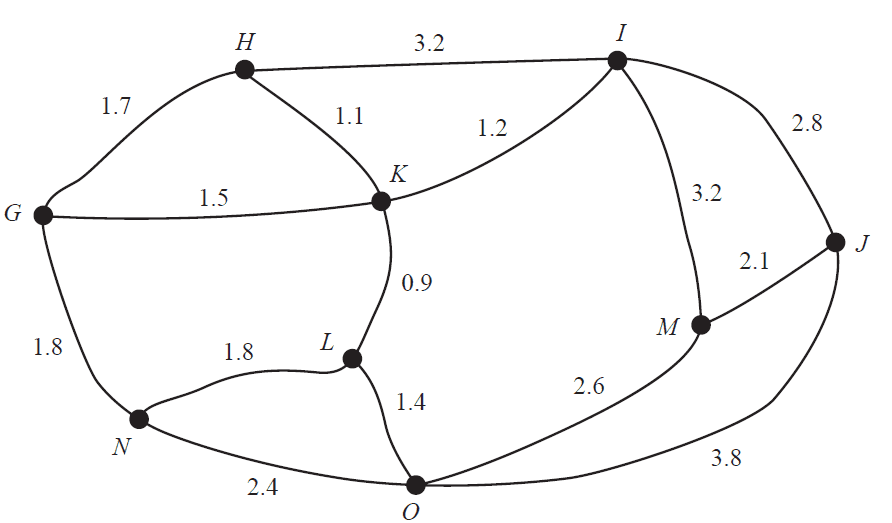
Three friends, Eden, Reynold and Shyla, meet at landmark \(G\).
a. Eden would like to visit landmark \(M\).
What is the minimum distance Eden could travel from \(G\) to \(M\)? 1 mark
b. Reynold would like to visit all the landmarks and return to \(G\).
Write down a route that Reynold could follow to minimise the total distance travelled. 1 mark
c. Shyla would like to travel along all the roads.
To complete this journey in the minimum distance, she will travel along two roads twice.
Shyla will leave from landmark \(G\) but end at a different landmark.
Complete the following by filling in the boxes provided.
The two roads that will be travelled along twice are the roads between:
- • vertex and vertex
- • vertex and vertex
One of the landmarks in state \(A\) requires a renovation project.
This project involves 12 activities, \(A\) to \(L\). The directed network below shows these activities and their completion times, in days.
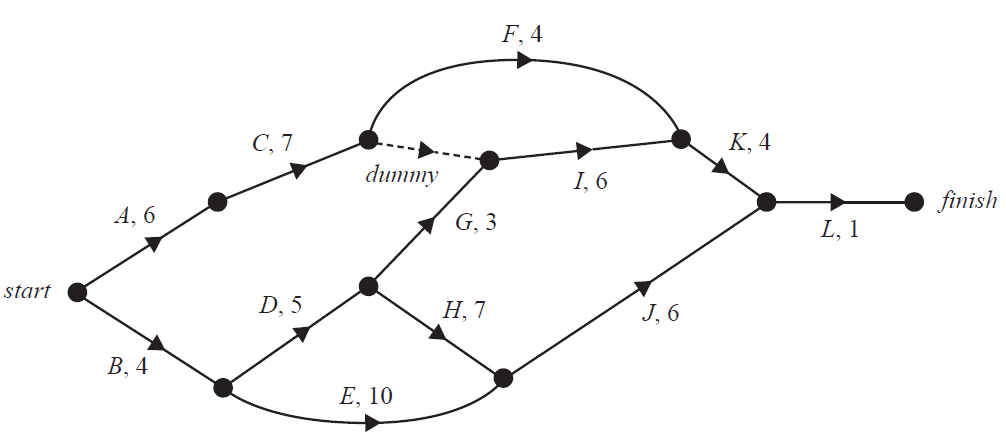
The table below shows the 12 activities that need to be completed for the renovation project.
It also shows the earliest start time (EST), the duration, and the immediate predecessors for the activities.
The immediate predecessor(s) for activity \(I\) and the EST for activity \(J\) are missing.
| Activity | EST | Duration | Immediate predecessor(s) |
|---|---|---|---|
| A | 0 | 6 | – |
| B | 0 | 4 | – |
| C | 6 | 7 | A |
| D | 4 | 5 | B |
| E | 4 | 10 | B |
| F | 13 | 4 | C |
| G | 9 | 3 | D |
| H | 9 | 7 | D |
| I | 13 | 6 | |
| J | 6 | E, H | |
| K | 19 | 4 | F, I |
| L | 23 | 1 | J, K |
a. Write down the immediate predecessor(s) for activity \(I\). 1 mark
b. What is the earliest start time, in days, for activity \(J\)? 1 mark
c. How many activities have a float time of zero? 1 mark
The managers of the project are able to reduce the time, in days, of six activities.
These reductions will result in an increase in the cost of completing the activity.
The maximum decrease in time of any activity is two days.
| Activity | A | B | F | H | I | K |
|---|---|---|---|---|---|---|
| Daily cost ($) | 1500 | 2000 | 2500 | 1000 | 1500 | 3000 |
d. If activities \(A\) and \(B\) have their completion time reduced by two days each, the overall completion time of the project will be reduced.
What will be the maximum reduction time, in days? 1 mark
e. The managers of the project have a maximum budget of $15 000 to reduce the time for several activities to produce the maximum reduction in the project’s overall completion time.
Complete the table below, showing the reductions in individual activity completion times that would achieve the earliest completion time within the $15 000 budget. 1 mark
| Activity | Reduction in completion time (0, 1 or 2 days) |
|---|---|
| A | |
| B | |
| F | |
| H | |
| I | |
| K |
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
