VCE General Maths Matrices 2024 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2024 - Exam 2
Vince works on a construction site.
The amount Vince gets paid depends on the type of shift he works, as shown in the table below.
| Shift type | Normal | Overtime | Weekend |
|---|---|---|---|
| Hourly rate of pay ($ per hour) | 36 | 54 | 72 |
This information is shown in matrix \(R\) below.
\(R = [36 \quad 54 \quad 72]\)
a. Matrix \(R^T\) is the transpose of matrix \(R\).
Write down matrix \(R^T\) in the space below. 1 mark
\(R^T = \)
During one week, Vince works 28 hours at the normal rate of pay, 6 hours at the overtime rate of pay, and 8 hours at the weekend rate of pay.
b. Complete the following matrix calculation showing the total amount Vince has been paid for this week. 1 mark
[ ] × \(R^{\mathrm{T}}\) = [ ]
c. Vince will receive $90 per hour if he works a public holiday shift.
Matrix \(Q\), as calculated below, can be used to show Vince’s hourly rate for each type of shift.
\(Q = n \times [1 \quad 1.5 \quad 2 \quad p] = [36 \quad 54 \quad 72 \quad 90]\)
Write the values of \(n\) and \(p\) in the boxes below. 1 mark
\(n = \)
\(p = \)
To access the southern end of the construction site, Vince must enter a security code consisting of five numbers.
The security code is represented by the row matrix \(W\).
The element in row \(i\) and column \(j\) of \(W\) is \(w_{ij}\).
The elements of \(W\) are determined by the rule \((i - j)^2 + 2j\).
a. Complete the following matrix showing the five numbers in the security code. 1 mark
\(W =\) [ ]
To access the northern end of the construction site, Vince enters a different security code, consisting of eight numbers.
This security code is represented by the row matrix \(X\).
The element in row \(i\) and column \(j\) of \(X\) is \(x_{ij}\).
The elements of \(X\) are also determined by the rule \((i - j)^2 + 2j\).
b. What is the last number in this security code to access the northern end of the construction site? 1 mark
A population of a native animal species lives near the construction site.
To ensure that the species is protected, information about the initial female population was collected at the beginning of 2023. The birth rates and the survival rates of the females in this population were also recorded.
This species has a life span of 4 years and the information collected has been categorised into four age groups: 0–1 year, 1–2 years, 2–3 years, and 3–4 years.
This information is displayed in the initial population matrix, \(R_0\), and the Leslie matrix, \(L\), below.
\[ R_0 = \begin{bmatrix} 70 \\ 80 \\ 90 \\ 40 \end{bmatrix} \quad L = \begin{bmatrix} 0.4 & 0.75 & 0.4 & 0 \\ 0.4 & 0 & 0 & 0 \\ 0 & 0.7 & 0 & 0 \\ 0 & 0 & 0.5 & 0 \end{bmatrix} \]
a. Using the information above
i. complete the following transition diagram. 1 mark

ii. complete the following table, showing the initial female population, and the predicted female population after one year, for each of the age groups. 1 mark
| Age group | ||||
|---|---|---|---|---|
| 0–1 year | 1–2 years | 2–3 years | 3–4 years | |
| Initial population | ||||
| Population after one year | ||||
b. It is predicted that if this species is not protected, the female population of each of the four age groups will rapidly decrease within the next 10 years.
After how many years is it predicted that the total female population of this species will first be half the initial female population? 1 mark
When the construction company established the construction site at the beginning of 2023, it employed 390 staff to work on the site.
The staff comprised 330 construction workers (\(C\)), 50 foremen (\(F\)) and 10 managers (\(M\)).
At the beginning of each year, staff can choose to stay in the same job, move to a different job on the site, or leave the site (\(L\)) and not return.
The transition diagram below shows the proportion of staff who are expected to change their job at the site each year.
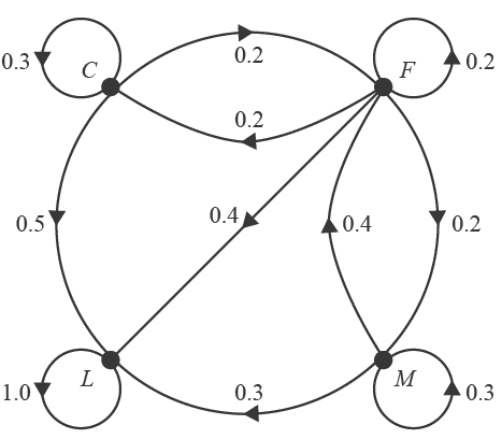
This situation can be modelled by the recurrence relation
\(S_{n+1} = TS_n\), where
\[ T \text{ is the transitional matrix, } S_0 = \begin{bmatrix} 330 \\ 50 \\ 10 \\ 0 \end{bmatrix} \begin{matrix} C \\ F \\ M \\ L \end{matrix} \text{ and } n \text{ is the number of years after 2023.} \]
a. Calculate the predicted percentage decrease in the number of foremen (\(F\)) on the site from 2023 to 2025. 1 mark
b. Determine the total number of staff on the site in the long term. 1 mark
To encourage more construction workers (\(C\)) to stay, the construction company has given workers an incentive to move into the job of foreman (\(F\)).
Matrix \(R\) below shows the ways in which staff are expected to change their jobs from year to year with this new incentive in place.
\[ \begin{array}{@{}c@{\,}c} & \begin{array}{@{}cccc@{}} C & F & M & L \end{array} \\ \begin{matrix} C \\ F \\ M \\ L \end{matrix} & \left[ \begin{array}{cccc} 0.4 & 0.2 & 0 & 0 \\ 0.4 & 0.2 & 0.4 & 0 \\ 0 & 0.2 & 0.3 & 0 \\ 0.2 & 0.4 & 0.3 & 1 \end{array} \right] \end{array} \]
The site always requires at least 330 construction workers.
To ensure that this happens, the company hires an additional 190 construction workers (\(C\)) at the beginning of 2024 and each year thereafter.
The matrix \(V_{n+1}\) will then be given by
\(V_{n+1} = RV_n + Z\), where
\[ V_0 = \begin{bmatrix} 330 \\ 50 \\ 10 \\ 0 \end{bmatrix} \begin{matrix} C \\ F \\ M \\ L \end{matrix} \quad Z = \begin{bmatrix} 190 \\ 0 \\ 0 \\ 0 \end{bmatrix} \begin{matrix} C \\ F \\ M \\ L \end{matrix} \text{ and } n \text{ is the number of years after 2023.} \]
c. How many more staff are there on the site in 2024 than there were in 2023? 1 mark
d. Based on this new model, the company has realised that in the long term there will be more than 200 foremen on site.
In which year will the number of foremen first be above 200? 1 mark
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
