VCE General Maths Matrices 2023 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2023
The daily maximum temperature at a regional town for two weeks is displayed in the table below.
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday | |
|---|---|---|---|---|---|---|---|
| Week 1 | 20 °C | 17 °C | 23 °C | 20 °C | 18 °C | 19 °C | 30 °C |
| Week 2 | 29 °C | 27 °C | 28 °C | 21 °C | 20 °C | 20 °C | 22 °C |
This information can also be represented by matrix \(M\), shown below.
\( M = \begin{bmatrix} 20 & 17 & 23 & 20 & 18 & 19 & 30 \\ 29 & 27 & 28 & 21 & 20 & 20 & 22 \end{bmatrix} \)
Element \(m_{21}\) indicates that
- A. the temperature was 29 °C on Monday in week 2.
- B. the temperature was 17 °C on Tuesday in week 1.
- C. the lowest temperature for these two weeks was 17 °C.
- D. the highest temperature for these two weeks was 29 °C.
- E. week 2 had a higher average maximum temperature than week 1.
Matrix \(P\) is a permutation matrix and matrix \(Q\) is a column matrix.
\( P = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} \quad Q = \begin{bmatrix} t \\ e \\ a \\ m \\ s \end{bmatrix} \)
When \(Q\) is multiplied by \(P\), which three letters change position?
- A. \(t, e, a\)
- B. \(e, a, m\)
- C. \(a, m, s\)
- D. \(m, s, t\)
- E. \(e, a, s\)
The following transition matrix, \(T\), models the movement of a species of bird around three different locations, \(M, N\) and \(O\) from one day to the next.
\[ T = \begin{array}{@{}c@{\,}c} & \begin{array}{@{}ccc@{}} M & N & O \end{array} \\ \begin{array}{c} M \\ N \\ O \end{array} & \left[ \begin{array}{ccc} \frac{1}{3} & 0 & \frac{9}{10} \\ \frac{1}{3} & 1 & \frac{1}{10} \\ \frac{1}{3} & 0 & 0 \end{array} \right] \end{array} \quad \textit{next day} \]Which one of the following statements best represents what will occur in the long term?
- A. No birds will remain at location M.
- B. No birds will remain at location N.
- C. All of the birds will end up at location M.
- D. All of the birds will end up at location O.
- E. An equal number of birds will be at all three locations.
Four table tennis teams played in a round-robin tournament. Each team played each other team once and there were no draws. The overall ranking of each team at the end of the tournament, based on number of wins, is shown in the table below.
| First | Unicorns (U) |
| Second | Vampires (V) |
| Third | Scorpions (S) |
| Fourth | Titans (T) |
A dominance matrix can display the results of each game, where a ‘1’ in the matrix shows that the team named in that row defeated the team named in that column. The dominance matrix for this tournament could be

Matrix \(K\) is a 3 × 2 matrix. The elements of \(K\) are determined by the rule \(k_{ij} = (i - j)^2\). Matrix \(K\) is
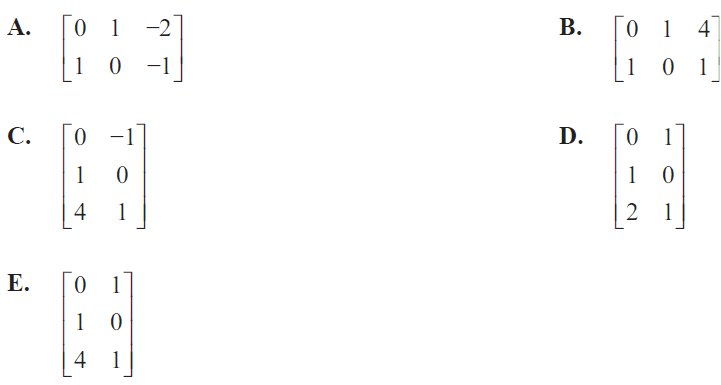
How many of the following statements are true?
- All square matrices have an inverse.
- The inverse of a matrix could be the same as the transpose of that matrix.
- If the determinant of a matrix is equal to zero, then the inverse does not exist.
- It is possible to take the inverse of an identity matrix.
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
A species of bird has a life span of three years. The females in this species do not reproduce in their first year but produce an average of four female offspring in their second year, and three in their third year.
The Leslie matrix, \(L\), below is used to model the female population distribution of this species of bird.
\( L = \begin{bmatrix} 0 & 4 & 3 \\ 0.2 & 0 & 0 \\ 0 & 0.4 & 0 \end{bmatrix} \)
The element in the second row, first column states that on average 20% of this population will
- A. be female.
- B. never reproduce.
- C. survive into their second year.
- D. produce offspring in their first year.
- E. live for the entire lifespan of three years.
For one particular week in a school year, students at Phyllis Island Primary School can spend their lunch break at the playground (\(P\)), basketball courts (\(B\)), oval (\(O\)) or the library (\(L\)). Students stay at the same location for the entire lunch break. The transition diagram below shows the proportion of students who change location from one day to the next.
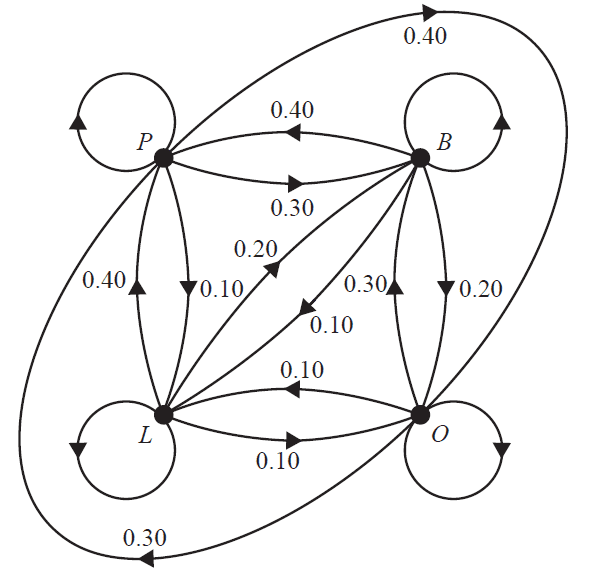
The transition diagram is incomplete. On the Monday, 150 students spent their lunch break at the playground, 50 students spent it at the basketball courts, 220 students spent it at the oval, and 40 students spent it in the library. Of the students expected to spend their lunch break on the oval on the Wednesday, the percentage of these students who also spent their lunch break on the oval on Tuesday is closest to
- A. 27%
- B. 30%
- C. 33%
- D. 47%
- E. 52%
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
