VCE General Maths Matrices 2022 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2022
Use the following information to answer Questions 1 and 2.
A bike rental business rents road bikes (\(R\)) and mountain bikes (\(M\)) in three sizes: child (\(C\)), junior (\(J\)) and adult (\(A\)).
Matrix \(B\) shows the daily rental cost, in dollars, for each type of bike.
\[ \begin{array}{r@{\hskip 1em}c} B = \begin{array}{c} \begin{array}{cc} R & M \end{array} \\[-1.2ex] \left[ \begin{array}{cc} 80 & 95 \\ 110 & 120 \\ 120 & 135 \end{array} \right] \end{array} & \begin{array}{c} \\[-1.2ex] % add vertical space above to match the top label height C \\ J \\ A \end{array} \end{array} \]The element in row \(i\) and column \(j\) in matrix \(B\) is \(b_{ij}\).
Question 1The daily cost of renting an adult mountain bike is shown in element
- A. \(b_{12}\)
- B. \(b_{21}\)
- C. \(b_{23}\)
- D. \(b_{31}\)
- E. \(b_{32}\)
On Sundays, the business increases the daily rental price for each type of bike by 10%.
To determine the rental cost for each type of bike on a Sunday, which one of the following matrix calculations needs to be completed?
- A. \(0.01B\)
- B. \(0.1B\)
- C. \(1.01B\)
- D. \(1.1B\)
- E. \(11B\)
Each day, members of a swim centre can choose to attend a morning session (\(M\)), an afternoon session (\(A\)) or no session (\(N\)).
The transition diagram below shows the transition from day to day.
The transition diagram is incomplete.
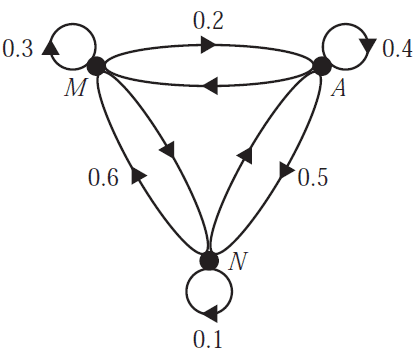
Which one of the following transition matrices represents this transition diagram?
The communication matrix below shows the communication links between five people: Steph (\(S\)), Tran (\(T\)), Ursula (\(U\)), Vinh (\(V\)) and Wanda (\(W\)).
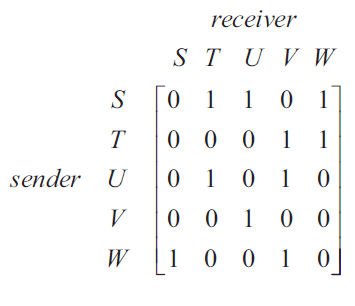
In this matrix:
- the '1' in row \(S\), column \(T\) indicates that Steph can communicate directly with Tran
- the '0' in row \(V\), column \(W\) indicates that Vinh cannot communicate directly with Wanda.
Ursula needs to communicate with Steph.
The sequence of communication links that will successfully allow Ursula to communicate with Steph is
- A. \(U-T-S\)
- B. \(U-W-S\)
- C. \(U-T-W-S\)
- D. \(U-V-T-S\)
- E. \(U-W-T-S\)
Matrix \(E\) is a \(2 \times 2\) matrix.
Matrix \(F\) is a \(2 \times 3\) matrix.
Matrix \(G\) is a \(3 \times 2\) matrix.
Matrix \(H\) is a \(3 \times 3\) matrix.
Which one of the following matrix products could have an inverse?
- A. \(EF\)
- B. \(FH\)
- C. \(GE\)
- D. \(GF\)
- E. \(HG\)
Matrix \(K\) is a permutation matrix.
\[ K = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \end{bmatrix} \]
Matrix \(M\) is a column matrix that is multiplied once by matrix \(K\) to obtain matrix \(P\).
When matrix \(M\) is multiplied by matrix \(K\), the element \(m_{31}\) moves to element
- A. \(p_{11}\)
- B. \(p_{21}\)
- C. \(p_{31}\)
- D. \(p_{41}\)
- E. \(p_{51}\)
Two types of computers – laptops (\(L\)) and desktops (\(D\)) – can be serviced by Henry (\(H\)), Irvine (\(I\)) or Jean (\(J\)).
Matrix \(N\) shows the time, in minutes, it takes each person to service a laptop and a desktop.
\[ \begin{array}{r@{\hskip 1em}c} N = & \begin{array}{c} \begin{array}{cc} L & D \end{array} \\[-1.2ex] \left[ \begin{array}{cc} 18 & 8 \\ 10 & 17 \\ 12 & 9 \end{array} \right] \end{array} \begin{array}{c} \\[-1.2ex] H \\ I \\ J \end{array} \end{array} \]Matrix \(Q\) shows the number of laptops and desktops in four different departments: marketing (\(M\)), advertising (\(A\)), publishing (\(P\)) and editing (\(E\)).
\[ \begin{array}{r@{\hskip 1em}c} Q = & \begin{array}{c} \begin{array}{cc} L & D \end{array} \\[-1.2ex] \left[ \begin{array}{cc} 6 & 8 \\ 4 & 7 \\ 5 & 5 \\ 10 & 12 \end{array} \right] \end{array} \begin{array}{c} \\[-1.2ex] M \\ A \\ P \\ E \end{array} \end{array} \]A calculation that determines the total time that it would take each of Henry, Irvine or Jean, working alone, to service all the laptops and desktops in all four departments is
- A. \([1 \quad 1 \quad 1 \quad 1] \times (Q \times N^T)\)
- B. \((Q \times N^T) \times \begin{bmatrix} 1 \\ 1 \end{bmatrix}\)
- C. \((N \times Q^T) \times Q\)
- D. \(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \times N \times Q^T\)
- E. \([1 \quad 1 \quad 1 \quad 1] \times Q \times N^T \times \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\)
Five competitors, Andy (\(A\)), Brie (\(B\)), Cleo (\(C\)), Della (\(D\)) and Eddie (\(E\)), participate in a darts tournament. Each competitor plays each of the other competitors once only, and each match results in a winner and a loser.
The matrix below shows the results of this darts tournament. There are still two matches that need to be played.
\[ \begin{array}{cc} & \textit{loser} \\ \textit{winner} & \begin{array}{c@{}c} & \begin{array}{@{}ccccc@{}} A & B & C & D & E \end{array} \\ \begin{matrix} A \\ B \\ C \\ D \\ E \end{matrix} & \left[ \begin{array}{@{}ccccc@{}} 0 & \dots & 0 & 1 & 0 \\ \dots & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & \dots & 1 \\ 0 & 1 & \dots & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \end{array} \right] \end{array} \end{array} \]
A '1' in the matrix shows that the competitor named in that row defeated the competitor named in that column. For example, the '1' in row 2, column 3 shows that Brie defeated Cleo. A '...' in the matrix shows that the competitor named in that row has not yet played the competitor named in that column.
The winner of this darts tournament is the competitor with the highest sum of their one-step and two-step dominances.
Which player, by winning their remaining match, will ensure that they are ranked first by the sum of their one-step and two-step dominances?
- A. Andy
- B. Brie
- C. Cleo
- D. Della
- E. Eddie
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
