VCE General Maths Matrices 2021 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2021
If matrix \( M = \begin{bmatrix} 3 & 2 \\ 8 & 9 \\ 13 & 7 \end{bmatrix} \), then its transpose, \(M^T\), is
- A. \( \begin{bmatrix} 2 & 3 \\ 9 & 8 \\ 7 & 13 \end{bmatrix} \)
- B. \( \begin{bmatrix} 2 & 9 & 7 \\ 3 & 8 & 13 \end{bmatrix} \)
- C. \( \begin{bmatrix} 7 & 9 & 2 \\ 13 & 8 & 3 \end{bmatrix} \)
- D. \( \begin{bmatrix} 3 & 8 & 13 \\ 2 & 9 & 7 \end{bmatrix} \)
- E. \( \begin{bmatrix} 13 & 8 & 3 \\ 7 & 9 & 2 \end{bmatrix} \)
Every Friday, the same number of workers from a large office building regularly purchase their lunch from one of two locations: the deli, \(D\), or the cafe, \(C\).
It has been found that:
- of the workers who purchase lunch from the deli on one Friday, 65% will return to purchase from the deli on the next Friday
- of the workers who purchase lunch from the cafe on one Friday, 55% will return to purchase from the cafe on the next Friday.
A transition matrix that can be used to describe this situation is

Ramon and Norma are names that contain the same letters but in a different order.
The permutation matrix that can change \( \begin{bmatrix} R \\ A \\ M \\ O \\ N \end{bmatrix} \) into \( \begin{bmatrix} N \\ O \\ R \\ M \\ A \end{bmatrix} \) is
- A. \( \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} \)
- B. \( \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{bmatrix} \)
- C. \( \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{bmatrix} \)
- D. \( \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{bmatrix} \)
- E. \( \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{bmatrix} \)
\(A\) is a \(7 \times 7\) matrix.
\(B\) is a \(10 \times 7\) matrix.
Which one of the following matrix expressions is defined?
- A. \(AB - 2B\)
- B. \(A(BA)^{-1}\)
- C. \(AB^2\)
- D. \(A^2 - BA\)
- E. \(A(B^T)\)
A fitness centre offers four different exercise classes: aerobics (\(A\)), boxfit (\(B\)), cardio (\(C\)) and dance (\(D\)). A customer’s choice of fitness class is expected to change from week to week according to the transition matrix \(P\), shown below.
\[ \begin{array}{r@{\hskip 1em}c} P = \begin{array}{c} \begin{array}{cccc} \textit{this week} \\ A & B & C & D \end{array} \\[-1.2ex] \left[ \begin{array}{cccc} 0.65 & 0 & 0.20 & 0.10 \\ 0 & 0.65 & 0.10 & 0.30 \\ 0.20 & 0.10 & 0.70 & 0 \\ 0.15 & 0.25 & 0 & 0.60 \end{array} \right] \end{array} & \begin{array}{c} \\[-1.2ex] \begin{matrix} A \\ B \\ C \\ D \end{matrix} & \textit{next week} \end{array} \end{array} \]An equivalent transition diagram has been constructed below, but the labelling is not complete.
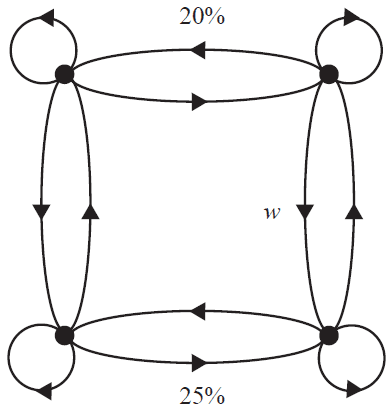
The proportion for one of the transitions is labelled \(w\). The value of \(w\) is
- A. 10%
- B. 15%
- C. 20%
- D. 25%
- E. 30%
The matrix \(S_{n+1}\) is determined from the matrix \(S_n\) using the recurrence relation \(S_{n+1} = T \times S_n - C\), where
\( T = \begin{bmatrix} 0.6 & 0.1 & 0.3 \\ 0.3 & 0.8 & 0.2 \\ 0.1 & 0.1 & 0.5 \end{bmatrix}, S_0 = \begin{bmatrix} 21 \\ 51 \\ 31 \end{bmatrix}, S_1 = \begin{bmatrix} 24.0 \\ 54.3 \\ 20.7 \end{bmatrix} \)
and \(C\) is a column matrix.
Matrix \(S_2\) is equal to
- A. \( \begin{bmatrix} 23.04 \\ 55.78 \\ 16.18 \end{bmatrix} \)
- B. \( \begin{bmatrix} 25.34 \\ 56.28 \\ 17.38 \end{bmatrix} \)
- C. \( \begin{bmatrix} 26.04 \\ 54.78 \\ 18.18 \end{bmatrix} \)
- D. \( \begin{bmatrix} 28.34 \\ 55.28 \\ 19.38 \end{bmatrix} \)
- E. \( \begin{bmatrix} 29.04 \\ 53.78 \\ 20.18 \end{bmatrix} \)
A new colony of endangered marsupials is established on a remote island. For one week, the marsupials can feed from only one of three feeding stations: \(A\), \(B\) or \(C\). On Monday, 50% of the marsupials were observed feeding at station \(A\) and 50% were observed feeding at station \(B\). No marsupials were observed feeding at station \(C\). The marsupials are expected to change their feeding stations each day this week according to the transition matrix \(T\).
\[ \begin{array}{r@{\hskip 1em}c} T = \begin{array}{c} \begin{array}{ccc} \textit{this day} \\ A & B & C \end{array} \\[-1.2ex] \left[ \begin{array}{ccc} 0.4 & 0.1 & 0.2 \\ 0.2 & 0.5 & 0.2 \\ 0.4 & 0.4 & 0.6 \end{array} \right] \end{array} & \begin{array}{c} \\[-1.2ex] \begin{matrix} A \\ B \\ C \end{matrix} & \textit{next day} \end{array} \end{array} \]Let \(S_n\) represent the state matrix showing the percentage of marsupials observed feeding at each feeding station \(n\) days after Monday of this week.
The matrix recurrence rule \(S_{n+1} = TS_n\) is used to model this situation.
From Tuesday to Wednesday, the percentage of marsupials who are not expected to change their feeding location is
- A. 44.5%
- B. 45%
- C. 50%
- D. 51.5%
- E. 52%
Consider the matrix recurrence relation below.
\[ S_0 = \begin{bmatrix} 30 \\ 20 \\ 40 \end{bmatrix}, \quad S_{n+1} = T S_n \quad \text{where} \quad T = \begin{bmatrix} j & 0.3 & l \\ 0.2 & m & 0.3 \\ 0.4 & 0.2 & n \end{bmatrix} \]
Matrix \(T\) is a regular transition matrix.
Given the information above and that \(S_1 = \begin{bmatrix} 42 \\ 28 \\ 20 \end{bmatrix}\), which one of the following is true?
- A. \(m > l\)
- B. \(j + l = 0.7\)
- C. \(j = n\)
- D. \(j > m\)
- E. \(l = m + n\)
The matrix \(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{bmatrix}\) is an example of
- A. a binary matrix.
- B. an identity matrix.
- C. a triangular matrix.
- D. a symmetric matrix.
- E. a permutation matrix.
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
