VCE General Maths Matrices 2020 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2020
The matrix \(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{bmatrix}\) is an example of
- A. a binary matrix.
- B. an identity matrix.
- C. a triangular matrix.
- D. a symmetric matrix.
- E. a permutation matrix.
Matrix \(A = \begin{bmatrix} 1 & 2 \\ 0 & 3 \\ 1 & 0 \\ 4 & 5 \end{bmatrix}\) and matrix \(B = \begin{bmatrix} 2 & 0 & 3 & 1 \\ 4 & 5 & 2 & 0 \end{bmatrix}\)
Matrix \(Q = A \times B\).
The element in row \(i\) and column \(j\) of matrix \(Q\) is \(q_{ij}\).
Element \(q_{41}\) is determined by the calculation
- A. \(0 \times 0 + 3 \times 5\)
- B. \(1 \times 1 + 2 \times 0\)
- C. \(1 \times 2 + 2 \times 4\)
- D. \(4 \times 1 + 5 \times 0\)
- E. \(4 \times 2 + 5 \times 4\)
Matrices \(P\) and \(W\) are defined below.
\[ P = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{bmatrix} \quad W = \begin{bmatrix} A \\ S \\ T \\ O \\ R \end{bmatrix} \]
If \(P^n \times W = \begin{bmatrix} A \\ S \\ T \\ O \\ R \end{bmatrix}\), the value of \(n\) could be
- A. 1
- B. 2
- C. 3
- D. 4
- E. 5
In a particular supermarket, the three top-selling magazines are Angel (\(A\)), Bella (\(B\)) and Crystal (\(C\)). The transition diagram below shows the way shoppers at this supermarket change their magazine choice from week to week.
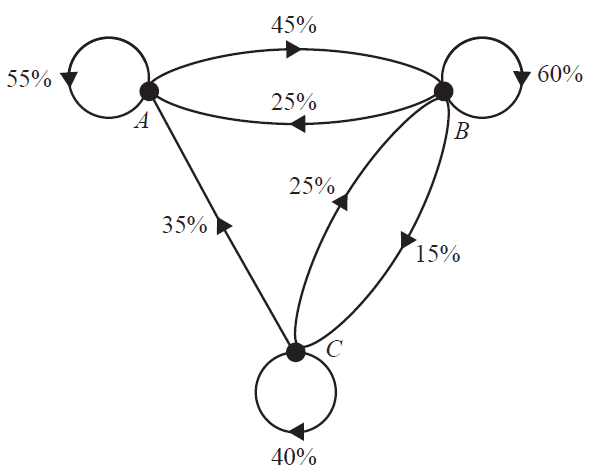
A transition matrix that provides the same information as the transition diagram is

The diagram below shows the direct communication links that exist between Sam (\(S\)), Tai (\(T\)), Umi (\(U\)) and Vera (\(V\)). For example, the arrow from Umi to Vera indicates that Umi can communicate directly with Vera.
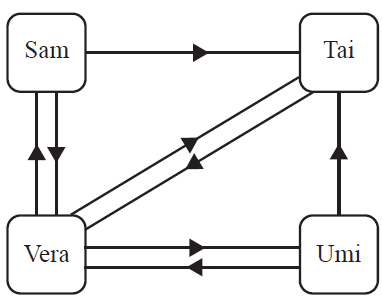
A communication matrix can be used to convey the same information.
In this matrix:
- a '1' indicates that a direct communication link exists between a sender and a receiver
- a '0' indicates that a direct communication link does not exist between a sender and a receiver.
The communication matrix could be
- A. \( \begin{array}{c@{\hskip 1em}c} \begin{array}{c} \\ \textit{sender} \\ \\ \end{array} & \begin{array}{c} \textit{receiver} \\ \begin{array}{cccc} S & T & U & V \end{array} \\ \left[ \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array} \right] \end{array} \end{array} \begin{array}{c} \\ S \\ T \\ U \\ V \end{array} \)
- B. \( \begin{array}{c@{\hskip 1em}c} \begin{array}{c} \\ \textit{sender} \\ \\ \end{array} & \begin{array}{c} \textit{receiver} \\ \begin{array}{cccc} S & T & U & V \end{array} \\ \left[ \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{array} \right] \end{array} \end{array} \begin{array}{c} \\ S \\ T \\ U \\ V \end{array} \)
- C. \( \begin{array}{c@{\hskip 1em}c} \begin{array}{c} \\ \textit{sender} \\ \\ \end{array} & \begin{array}{c} \textit{receiver} \\ \begin{array}{cccc} S & T & U & V \end{array} \\ \left[ \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \end{array} \right] \end{array} \end{array} \begin{array}{c} \\ S \\ T \\ U \\ V \end{array} \)
- D. \( \begin{array}{c@{\hskip 1em}c} \begin{array}{c} \\ \textit{sender} \\ \\ \end{array} & \begin{array}{c} \textit{receiver} \\ \begin{array}{cccc} S & T & U & V \end{array} \\ \left[ \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{array} \right] \end{array} \end{array} \begin{array}{c} \\ S \\ T \\ U \\ V \end{array} \)
- E. \( \begin{array}{c@{\hskip 1em}c} \begin{array}{c} \\ \textit{sender} \\ \\ \end{array} & \begin{array}{c} \textit{receiver} \\ \begin{array}{cccc} S & T & U & V \end{array} \\ \left[ \begin{array}{cccc} 0 & 1 & 0 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 2 \\ 2 & 2 & 2 & 0 \end{array} \right] \end{array} \end{array} \begin{array}{c} \\ S \\ T \\ U \\ V \end{array} \)
The element in row \(i\) and column \(j\) of matrix \(M\) is \(m_{ij}\).
\(M\) is a \(3 \times 3\) matrix. It is constructed using the rule \(m_{ij} = 3i + 2j\).
\(M\) is
- A. \(\begin{bmatrix} 5 & 7 & 9 \\ 7 & 9 & 11 \\ 11 & 13 & 15 \end{bmatrix}\)
- B. \(\begin{bmatrix} 5 & 7 & 9 \\ 8 & 10 & 12 \\ 11 & 13 & 15 \end{bmatrix}\)
- C. \(\begin{bmatrix} 5 & 7 & 10 \\ 8 & 10 & 13 \\ 11 & 13 & 16 \end{bmatrix}\)
- D. \(\begin{bmatrix} 5 & 8 & 11 \\ 7 & 10 & 13 \\ 9 & 12 & 15 \end{bmatrix}\)
- E. \(\begin{bmatrix} 5 & 8 & 11 \\ 8 & 11 & 14 \\ 11 & 14 & 17 \end{bmatrix}\)
A small shopping centre has two coffee shops: Fatima's (\(F\)) and Giorgio's (\(G\)). The percentage of coffee-buyers at each shop changes from day to day, as shown in the transition matrix \(T\).
\[ T = \begin{array}{c} \begin{array}{cc} F & G \end{array} \\ \begin{bmatrix} 0.85 & 0.35 \\ 0.15 & 0.65 \end{bmatrix} \end{array} \begin{matrix} F \\ G \end{matrix} \quad \text{tomorrow} \]
On a particular Monday, 40% of coffee-buyers bought their coffees at Fatima's.
The matrix recursion relation \(S_{n+1} = T S_n\) is used to model this situation.
The percentage of coffee-buyers who are expected to buy their coffee at Giorgio's on Friday of the same week is closest to
- A. 31%
- B. 32%
- C. 34%
- D. 45%
- E. 68%
The table below shows information about three matrices: \(A\), \(B\) and \(C\).
| Matrix | Order |
|---|---|
| \(A\) | \(2 \times 4\) |
| \(B\) | \(2 \times 3\) |
| \(C\) | \(3 \times 4\) |
The transpose of matrix \(A\), for example, is written as \(A^T\).
What is the order of the product \(C^T \times (A^T \times B)^T\)?
- A. \(2 \times 3\)
- B. \(3 \times 4\)
- C. \(4 \times 2\)
- D. \(4 \times 3\)
- E. \(4 \times 4\)
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
