VCE General Maths Matrices 2019 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2019 - Exam 2
The car park at a theme park has three areas, \(A\), \(B\) and \(C\).
The number of empty (\(E\)) and full (\(F\)) parking spaces in each of the three areas at 1 pm on Friday are shown in matrix \(Q\) below.
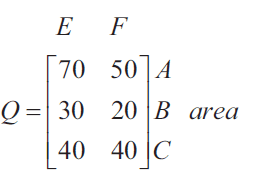
a. What is the order of matrix \(Q\)? 1 mark
b. Write down a calculation to show that 110 parking spaces are full at 1 pm. 1 mark
Drivers must pay a parking fee for each hour of parking.
Matrix \(P\), below, shows the hourly fee, in dollars, for a car parked in each of the three areas.
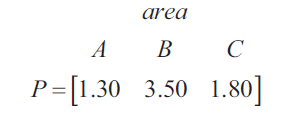
c. The total parking fee, in dollars, collected from these 110 parked cars if they were parked for one hour is calculated as follows.
\(P \times L = [207.00]\)
where matrix \(L\) is a \(3 \times 1\) matrix.
Write down matrix \(L\). 1 mark
\(L = \)
The number of whole hours that each of the 110 cars had been parked was recorded at 1 pm. Matrix \(R\), below, shows the number of cars parked for one, two, three or four hours in each of the areas \(A\), \(B\) and \(C\).
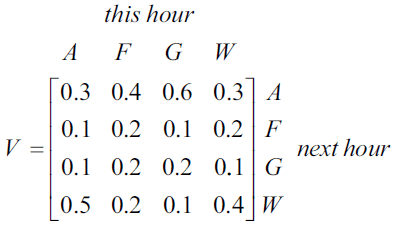
d. Matrix \(R^T\) is the transpose of matrix \(R\).
Complete the matrix \(R^T\) below. 1 mark

e. Explain what the element in row 3, column 2 of matrix \(R^T\) represents. 1 mark
The theme park has four locations, Air World (\(A\)), Food World (\(F\)), Ground World (\(G\)) and Water World (\(W\)).
The number of visitors at each of the four locations is counted every hour.
By 10 am on Saturday the park had reached its capacity of 2000 visitors and could take no more visitors.
The park stayed at capacity until the end of the day.
The state matrix, \(S_0\), below, shows the number of visitors at each location at 10 am on Saturday.
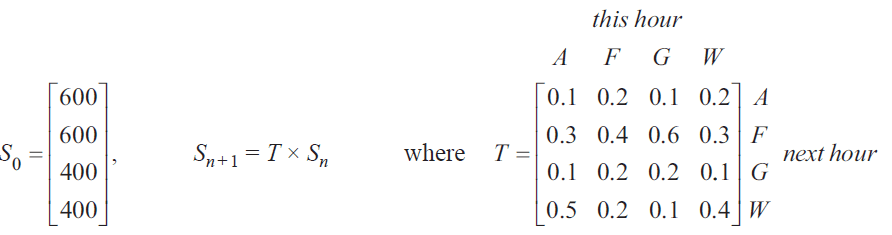
a. What percentage of the park’s visitors were at Water World (\(W\)) at 10 am on Saturday? 1 mark
Let \(S_n\) be the state matrix that shows the number of visitors expected at each location \(n\) hours after 10 am on Saturday.
The number of visitors expected at each location \(n\) hours after 10 am on Saturday can be determined by the matrix recurrence relation below.
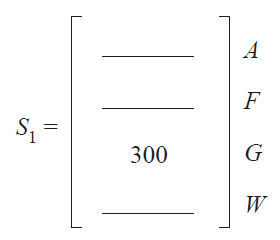
b. Complete the state matrix, \(S_1\), below to show the number of visitors expected at each location at 11 am on Saturday. 1 mark
\(S_1 = \)
c. Of the 300 visitors expected at Ground World (\(G\)) at 11 am, what percentage was at either Air World (\(A\)) or Food World (\(F\)) at 10 am? 1 mark
d. The proportion of visitors moving from one location to another each hour on Sunday is different from Saturday.
Matrix \(V\), below, shows the proportion of visitors moving from one location to another each hour after 10 am on Sunday.
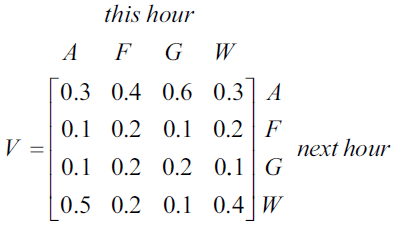
Matrix \(V\) is similar to matrix \(T\) but has the first two rows of matrix \(T\) interchanged.
The matrix product that will generate matrix \(V\) from matrix \(T\) is
\(V = M \times T\)
where matrix \(M\) is a binary matrix.
Write down matrix \(M\). 1 mark
\(M = \)
On Sunday, matrix \(V\) is used when calculating the expected number of visitors at each location every hour after 10 am. It is assumed that the park will be at its capacity of 2000 visitors for all of Sunday.
Let \(L_0\) be the state matrix that shows the number of visitors at each location at 10 am on Sunday.
The number of visitors expected at each location at 11 am on Sunday can be determined by the matrix product
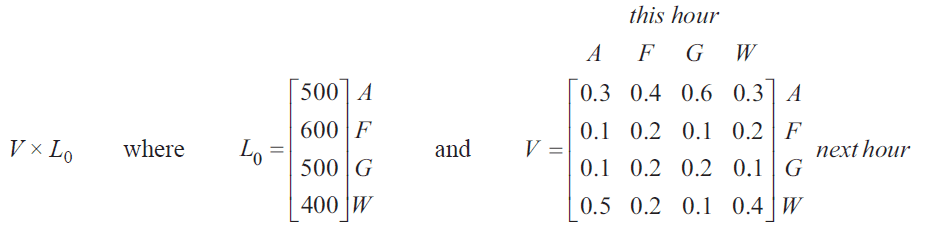
a. Safety restrictions require that all four locations have a maximum of 600 visitors.
Which location is expected to have more than 600 visitors at 11 am on Sunday? 1 mark
b. Whenever more than 600 visitors are expected to be at a location on Sunday, the first 600 visitors can stay at that location and all others will be moved directly to Ground World (\(G\)).
State matrix \(R_n\) contains the number of visitors at each location \(n\) hours after 10 am on Sunday, after the safety restrictions have been enforced.
Matrix \(R_1\) can be determined from the matrix recurrence relation
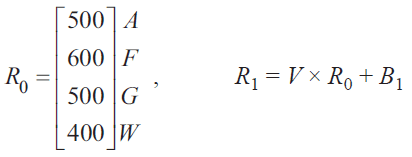
where matrix \(B_1\) shows the required movement of visitors at 11 am.
i. Determine the matrix \(B_1\). 1 mark
\(B_1 = \)
ii. State matrix \(R_2\) can be determined from the new matrix rule
\(R_2 = V R_1 + B_2\)
where matrix \(B_2\) shows the required movement of visitors at 12 noon.
Determine the state matrix \(R_2\). 1 mark
\(R_2 = \)
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
