VCE General Maths Matrices 2019 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 7
Reading time: 2.5 minutes
Writing time: 16 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2019
Consider the following four matrix expressions.
\( \begin{bmatrix} 8 \\ 12 \end{bmatrix} + \begin{bmatrix} 4 \\ 2 \end{bmatrix} \)
\( \begin{bmatrix} 8 & 4 \\ 12 & 0 \end{bmatrix} + \begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
\( \begin{bmatrix} 8 & 0 \\ 12 & 0 \end{bmatrix} + \begin{bmatrix} 4 \\ 2 \end{bmatrix} \)
\( \begin{bmatrix} 8 & 0 \\ 12 & 0 \end{bmatrix} + \begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
How many of these four matrix expressions are defined?
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
There are two rides called The Big Dipper and The Terror Train at a carnival.
The cost, in dollars, for a child to ride on each ride is shown in the table below.
| Ride | Cost ($) |
| The Big Dipper | 7 |
| The Terror Train | 8 |
Six children ride once only on The Big Dipper and once only on The Terror Train.
The total cost of the rides, in dollars, for these six children can be determined by which one of the following calculations?
- A. \( \times [7 \quad 8] \)
- B. \( \times \begin{bmatrix} 7 \\ 8 \end{bmatrix} \)
- C. \( [6 \quad 6] \times [7 \quad 8] \)
- D. \( [6 \quad 6] \times \begin{bmatrix} 7 \\ 8 \end{bmatrix} \)
- E. \( \begin{bmatrix} 6 \\ 6 \end{bmatrix} \times [7 \quad 8] \)
Consider the matrix \(P\), where \( P = \begin{bmatrix} 3 & 2 & 1 \\ 5 & 4 & 3 \end{bmatrix} \)
The element in row \(i\) and column \(j\) of matrix \(P\) is \(p_{ij}\).
The elements in matrix \(P\) are determined by the rule
- A. \( p_{ij} = 4 - j \)
- B. \( p_{ij} = 2i + 1 \)
- C. \( p_{ij} = i + j + 1 \)
- D. \( p_{ij} = i + 2j \)
- E. \( p_{ij} = 2i - j + 2 \)
Stella completed a multiple-choice test that had 10 questions.
Each question had five possible answers, A, B, C, D and E.
For question number one, Stella chose the answer E.
Stella chose each of the nine remaining answers, in order, by following the transition matrix, \(T\), below.
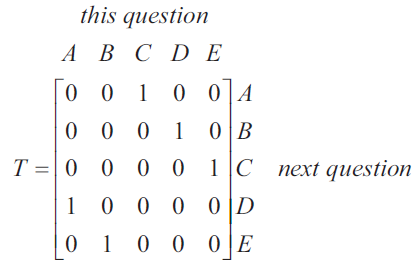
What answer did Stella choose for question number six?
- A. A
- B. B
- C. C
- D. D
- E. E
A water park is open from 9 am until 5 pm.
There are three activities, the pool (\(P\)), the slide (\(S\)) and the water jets (\(W\)), at the water park.
Children have been found to change their activity at the water park each half hour, as shown in the transition matrix, \(T\), below.
\[ \begin{array}{r@{\hskip 1em}c} T = \begin{array}{c} \begin{array}{ccc} \textit{P} & \textit{S} & \textit{W} \end{array} \\[-1.2ex] \left[ \begin{array}{ccc} 0.80 & 0.20 & 0.40 \\ 0.05 & 0.60 & 0.10 \\ 0.15 & 0.20 & 0.50 \end{array} \right] \end{array} & \begin{array}{c} \textit{this half hour} \\[-1.2ex] \textit{P} \\ \textit{S} \\ \textit{W} \end{array} \quad \textit{next half hour} \end{array} \]
A group of children has come to the water park for the whole day.
The percentage of these children who are expected to be at the slide (\(S\)) at closing time is closest to
- A. 14%
- B. 20%
- C. 24%
- D. 25%
- E. 62%
The communication matrix below shows the direct paths by which messages can be sent between two people in a group of six people, \(U\) to \(Z\).

A '1' in the matrix shows that the person named in that row can send a message directly to the person named in that column.
For example, the '1' in row 4, column 2 shows that \(X\) can send a message directly to \(V\).
In how many ways can \(Y\) get a message to \(W\) by sending it directly to one other person?
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
An airline parks all of its planes at Sydney airport or Melbourne airport overnight.
The transition diagram below shows the change in the location of the planes from night to night.
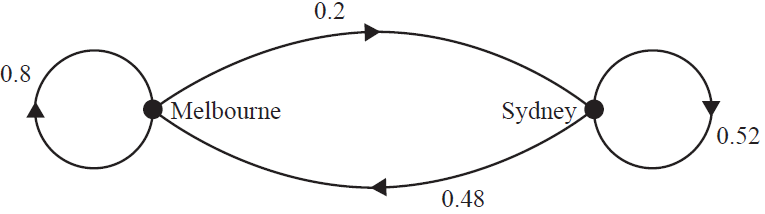
There are always \(m\) planes parked at Melbourne airport.
There are always \(s\) planes parked at Sydney airport.
Of the planes parked at Melbourne airport on Tuesday night, 12 had been parked at Sydney airport on Monday night.
How many planes does the airline have?
- A. 25
- B. 37
- C. 62
- D. 65
- E. 85
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

