VCE General Maths Matrices 2017 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2017 - Exam 2 (Part 1)
A school canteen sells pies (P), rolls (R) and sandwiches (S).
The number of each item sold over three school weeks is shown in matrix \(M\).
\[ M = \begin{array}{c} \begin{array}{ccc} \text{P} & \text{R} & \text{S} \end{array} \\ \begin{bmatrix} 35 & 24 & 60 \\ 28 & 32 & 43 \\ 32 & 30 & 56 \end{bmatrix} \end{array} \begin{array}{l} \text{week 1} \\ \text{week 2} \\ \text{week 3} \end{array} \]a. In total, how many sandwiches were sold in these three weeks? 1 mark
The element in row \(i\) and column \(j\) of matrix \(M\) is \(m_{ij}\).
b. What does the element \(m_{12}\) indicate? 1 mark
c. Consider the matrix equation
\[ \begin{bmatrix} 35 & 24 & 60 \\ 28 & 32 & 43 \\ 32 & 30 & 56 \end{bmatrix} \times \begin{bmatrix} a \\ b \\ c \end{bmatrix} = \begin{bmatrix} 491.55 \\ 428.00 \\ 487.60 \end{bmatrix} \]where \(a\) = cost of one pie, \(b\) = cost of one roll and \(c\) = cost of one sandwich.
i. What is the cost of one sandwich? 1 mark
ii. The matrix equation below shows that the total value of all rolls and sandwiches sold in these three weeks is $915.60
\[ L \times \begin{bmatrix} 491.55 \\ 428.00 \\ 487.60 \end{bmatrix} = [915.60] \]Matrix \(L\) in this equation is of order \(1 \times 3\).
Write down matrix \(L\). 1 mark
]
Junior students at this school must choose one elective activity in each of the four terms in 2018.
Students can choose from the areas of performance (P), sport (S) and technology (T).
The transition diagram below shows the way in which junior students are expected to change their choice of elective activity from term to term.
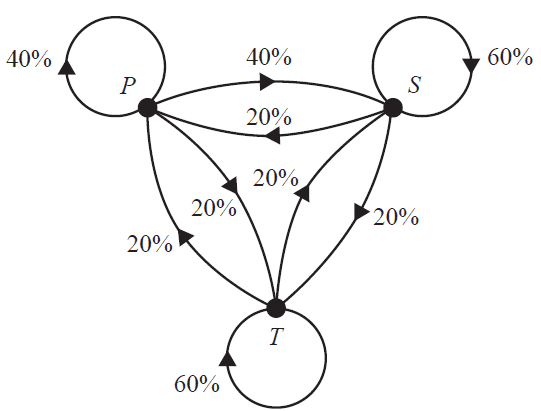
a. Of the junior students who choose performance (P) in one term, what percentage are expected to choose sport (S) the next term? 1 mark
Matrix \(J_1\) lists the number of junior students who will be in each elective activity in Term 1.
\[ J_1 = \begin{bmatrix} 300 \\ 240 \\ 210 \end{bmatrix} \begin{array}{c} \text{P} \\ \text{S} \\ \text{T} \end{array} \]b. 306 junior students are expected to choose sport (S) in Term 2.
Complete the calculation below to show this. 1 mark
\(300 \times \) \( + 240 \times \) \( + 210 \times \) \( = 306\)
c. In Term 4, how many junior students in total are expected to participate in performance (P) or sport (S) or technology (T)? 1 mark
Senior students at this school will also choose one elective activity in each of the four terms in 2018.
Their choices are communication (C), investigation (I), problem-solving (P) and service (S).
The transition matrix \(T\) shows the way in which senior students are expected to change their choice of elective activity from term to term.
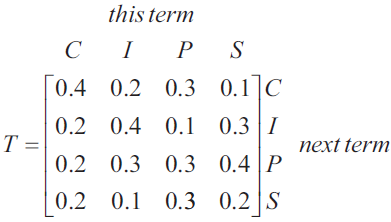
Let \(S_n\) be the state matrix for the number of senior students expected to choose each elective activity in Term \(n\).
For the given matrix \(S_1\), a matrix rule that can be used to predict the number of senior students in each elective activity in Terms 2, 3 and 4 is
\[ S_1 = \begin{bmatrix} 300 \\ 200 \\ 200 \\ 300 \end{bmatrix}, \quad S_{n+1} = TS_n \]a. How many senior students will not change their elective activity from Term 1 to Term 2? 1 mark
b. Complete \(S_2\), the state matrix for Term 2, below. 1 mark
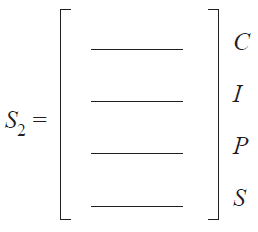
c. Of the senior students expected to choose investigation (I) in Term 3, what percentage chose service (S) in Term 2? 2 marks
d. What is the maximum number of senior students expected in investigation (I) at any time during 2018? 1 mark
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
