2024 VCAA Maths Methods Exam 1
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 40
Reading time: 15 minutes
Writing time: 1 hours
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Let \( y = e^x \cos(3x) \).
Find \( \frac{dy}{dx} \). 1 mark
b. Let \( f(x) = \log_e(x^3 - 3x + 2) \). Find \( f'(3) \). 2 marks
Consider the simultaneous linear equations
\( 3k x - 2y = k + 4 \)
\( (k - 4)x + ky = -k \)
where \( x, y \in \mathbb{R} \) and \( k \) is a real constant.
Determine the value of \( k \) for which the system of equations has no real solution. 3 marks
Let \( g : \mathbb{R} \setminus \{-3\} \rightarrow \mathbb{R},\ g(x) = \frac{1}{x + 3} - 2 \).
a. On the axes below, sketch the graph of \( y = g(x) \), labelling all asymptotes with their equations and axis intercepts with their coordinates. 2 marks
b. Determine the area of the region bounded by the line \( x = -2 \), the x-axis, the y-axis and the graph of \( y = g(x) \). 3 marks
Let \( X \) be a binomial random variable where \( X \sim \text{Bi}\left(4, \frac{9}{10}\right) \).
a. Find the standard deviation of \( X \). 1 mark
b. Find \( \Pr(X < 2) \). 2 marks
The function \( h : [0, \infty) \rightarrow \mathbb{R},\ h(t) = \frac{3000}{t + 1} \) models the population of a town after \( t \) years.
a. Use the model \( h(t) \) to predict the population of the town after four years. 1 mark
b. A new function, \( h_1 \), models a population where \( h_1(0) = h(0) \) but \( h_1 \) decreases at half the rate of \( h \) at any point in time.
State a sequence of two transformations that maps \( h \) to this new model \( h_1 \). 2 marks
c. In the town, 100 people were randomly selected and surveyed, with 60 people indicating that they were unhappy with the roads.
i. Determine an approximate 95% confidence interval for the proportion of people in the town who are unhappy with the roads. Use \( z = 2 \) for this confidence interval. 2 marks
ii. A new sample of \( n \) people results in the same sample proportion.
Find the smallest value of \( n \) to achieve a standard deviation of \( \frac{\sqrt{2}}{50} \) for the sample proportion. 1 mark
Solve \( 2\log_3(x - 4) + \log_3(x) = 2 \) for \( x \). 4 marks
Part of the graph of \( f : [-\pi, \pi] \rightarrow \mathbb{R},\ f(x) = x\sin(x) \) is shown below.
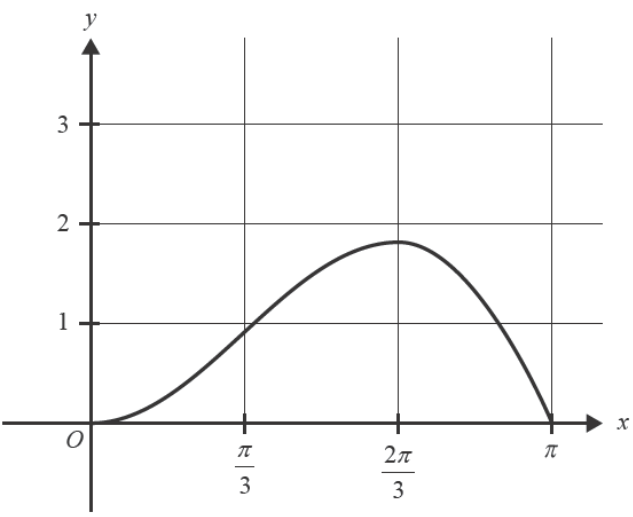
a. Use the trapezium rule with a step size of \( \frac{\pi}{3} \) to determine an approximation of the total area between the graph of \( y = f(x) \) and the x-axis over the interval \( x \in [0, \pi] \). 3 marks
b.
i. Find \( f'(x) \). 1 mark
ii. Determine the range of \( f'(x) \) over the interval \( \left[\frac{\pi}{3}, \frac{2\pi}{3} \right] \). 1 mark
iii. Hence, verify that \( f(x) \) has a stationary point for \( x \in \left[\frac{\pi}{3}, \frac{2\pi}{3} \right] \). 1 mark
c. On the set of axes below, sketch the graph of \( y = f'(x) \) on the domain \( [-\pi, \pi] \), labelling the endpoints with their coordinates.
You may use the fact that the graph of \( y = f'(x) \) has a local minimum at approximately \( (-1.1, -1.4) \) and a local maximum at approximately \( (1.1, 1.4) \). 3 marks
Let \( g : \mathbb{R} \rightarrow \mathbb{R}, \quad g(x) = \sqrt[3]{x - k}+ m, \quad \text{where } k \in \mathbb{R} \setminus \{0\} \text{ and } m \in \mathbb{R} \).
Let the point \( P \) be the y-intercept of the graph of \( y = g(x) \).
a. Find the coordinates of \( P \), in terms of \( k \) and \( m \). 1 mark
b. Find the gradient of \( g \) at \( P \), in terms of \( k \). 2 marks
c. Given that the graph of \( y = g(x) \) passes through the origin, express \( k \) in terms of \( m \). 1 mark
d. Let the point \( Q \) be a point different from the point \( P \), such that the gradient of \( g \) at points \( P \) and \( Q \) are equal.
Given that the graph of \( y = g(x) \) passes through the origin, find the coordinates of \( Q \) in terms of \( m \). 3 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

