2023 VCAA Maths Methods Sample Exam 2

\(x - 2y = 3\)
\(2y - z = 4\)

Which one of the following correctly describes the general solution to the system of linear equations given above?

• A. \(x = k, y = \frac{1}{2}(k + 3), z = k - 1,\) for all \(k \in R\)
• B. \(x = k, y = \frac{1}{2}(k + 3), z = k + 1,\) for all \(k \in R\)
• C. \(x = k, y = \frac{1}{2}(k - 3), z = k + 7,\) for all \(k \in R\)
• D. \(x = k, y = \frac{1}{2}(k - 3), z = k - 7,\) for all \(k \in R\)
• E. \(x = k, y = \frac{1}{2}(k + 3), z = k - 7,\) for all \(k \in R\)

Newton's method is being used to approximate the non-zero \(x\)-intercept of the function with the equation \(f(x) = \frac{x^3}{5} - \sqrt{x}\). An initial estimate of \(x_0 = 1\) is used.

Which one of the following gives the first estimate that would correctly approximate the intercept to three decimal places?

• A. \(x_6\)
• B. \(x_7\)
• C. \(x_8\)
• D. \(x_9\)
• E. The intercept cannot be correctly approximated using Newton's method.

The area between the curve \(y = \frac{1}{27}(x - 3)^2(x + 3)^2 + 1\) and the \(x\)-axis on the interval \(x \in [0, 4]\) has been approximated using the trapezium rule, as shown in the graph below.

Using the trapezium rule, the approximate area calculated is equal to

• A. \(\frac{1}{2}\left(4+\frac{91}{27}+\frac{52}{27}+1+\frac{76}{27}\right)\)
• B. \(\frac{1}{2}\left(4+\frac{182}{27}+\frac{104}{27}+2+\frac{76}{27}\right)\)
• C. \(\frac{1}{2}\left(8+\frac{182}{27}+\frac{104}{27}+2+\frac{152}{27}\right)\)
• D. \(\frac{1}{2}\left(\frac{182}{27}+\frac{104}{27}+2+\frac{76}{27}\right)\)
• E. \(\frac{1}{2}\left(8+\frac{182}{27}+\frac{104}{27}+2\right)\)

The probability density function \(f\) of a random variable \(X\) is given by

\( f(x) = \begin{cases} \frac{x+1}{20} & 0 \le x < 4 \\ \frac{36-5x}{64} & 4 \le x \le 7.2 \\ 0 & \text{elsewhere} \end{cases} \)

The value of \(a\) such that \(\Pr(X \le a) = \frac{5}{8}\) is

• A. \(\frac{4(\sqrt{15}-9)}{5}\)
• B. \(\sqrt{26}-1\)
• C. \(\frac{36-4\sqrt{15}}{5}\)
• D. \(\frac{4\sqrt{15}+9}{5}\)
• E. \(\frac{4\sqrt{15}+36}{5}\)

The algorithm below, described in pseudocode, estimates the value of a definite integral using the trapezium rule.

Consider the algorithm implemented with the following inputs.

trapezium(\(\log_e(x)\), 1, 3, 10)

The value of the variable sum after one iteration of the While loop would be closest to

• A. 1.281
• B. 1.289
• C. 1.463
• D. 1.617
• E. 2.136

Consider the algorithm below, which uses the bisection method to estimate the solution to an equation in the form \(f(x) = 0\).

The algorithm is implemented as follows.

bisection(\(\sin(x)\), 3, 5, 2)

Which value would be returned when the algorithm is implemented as given?

• A. -0.351
• B. -0.108
• C. 3.25
• D. 3.5
• E. 4

One way of implementing Newton's method using pseudocode, with a tolerance level of 0.001, is shown below.

The pseudocode is incomplete, with two missing lines indicated by an empty box.

Which one of the following options would be most appropriate to fill the empty box?

• A.
  If next_x - prev_x < 0.001 Then
    Return prev_x
• B.
  If next_x - prev_x < 0.001 Then
    Return next_x
• C.
  If prev_x - next_x < 0.001 Then
    Return next_x
• D.
  If -0.001 < next_x - prev_x < 0.001 Then
    Return prev_x
• E.
  If -0.001 < next_x - prev_x < 0.001 Then
    Return next_x

The function \(g\) is defined as follows.

\(g : (0, 7] \rightarrow \mathbb{R}, g(x) = 3 \log_e(x) - x\)

a. Sketch the graph of \(g\) on the axes below. Label the vertical asymptote with its equation, and label any axial intercepts, stationary points and endpoints in coordinate form, correct to three decimal places. 3 marks

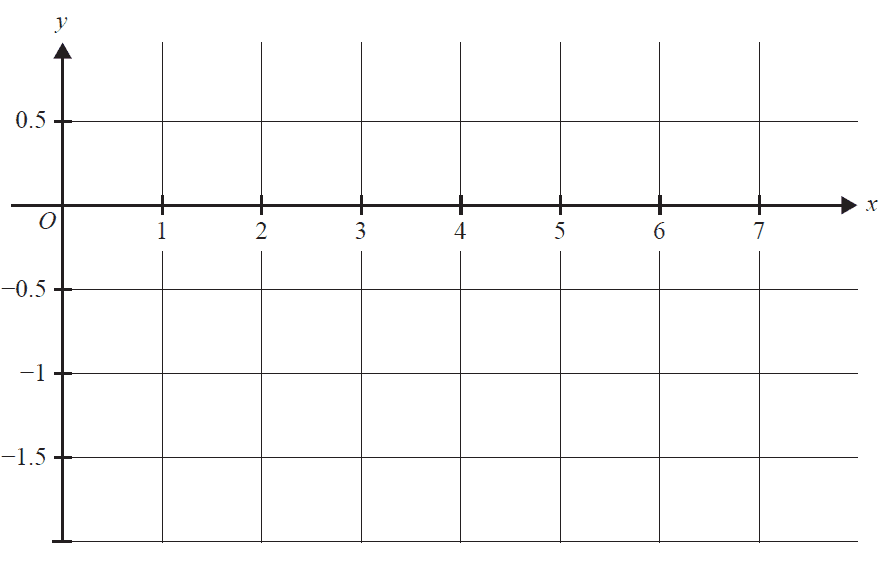
b.

i. Find the equation of the tangent to the graph of \(g\) at the point where \(x = 1\). 1 mark

ii. Sketch the graph of the tangent to the graph of \(g\) at \(x = 1\) on the axes in part a. 1 mark

Newton's method is used to find an approximate \(x\)-intercept of \(g\), with an initial estimate of \(x_0 = 1\).

c. Find the value of \(x_1\). 1 mark

d. Find the horizontal distance between \(x_1\) and the closest \(x\)-intercept of \(g\), correct to four decimal places. 1 mark

e.

i. Find the value of \(k\), where \(k > 1\), such that an initial estimate of \(x_0 = k\) gives the same value of \(x_1\) as found in part c. Give your answer correct to three decimal places. 2 marks

ii. Using this value of \(k\), sketch the tangent to the graph of \(g\) at the point where \(x = k\) on the axes in part a. 1 mark

Jac and Jill have built a ramp for their toy car. They will release the car at the top of the ramp and the car will jump off the end of the ramp.

The cross-section of the ramp is modelled by the function \(f\), where

\( f(x) = \begin{cases} 40 & 0 \le x < 5 \\ \frac{1}{800}(x^3 - 75x^2 + 675x + 30375) & 5 \le x \le 55 \end{cases} \)

\(f(x)\) is both smooth and continuous at \(x = 5\).

The graph of \(y = f(x)\) is shown below, where \(x\) is the horizontal distance from the start of the ramp and \(y\) is the height of the ramp. All lengths are in centimetres.

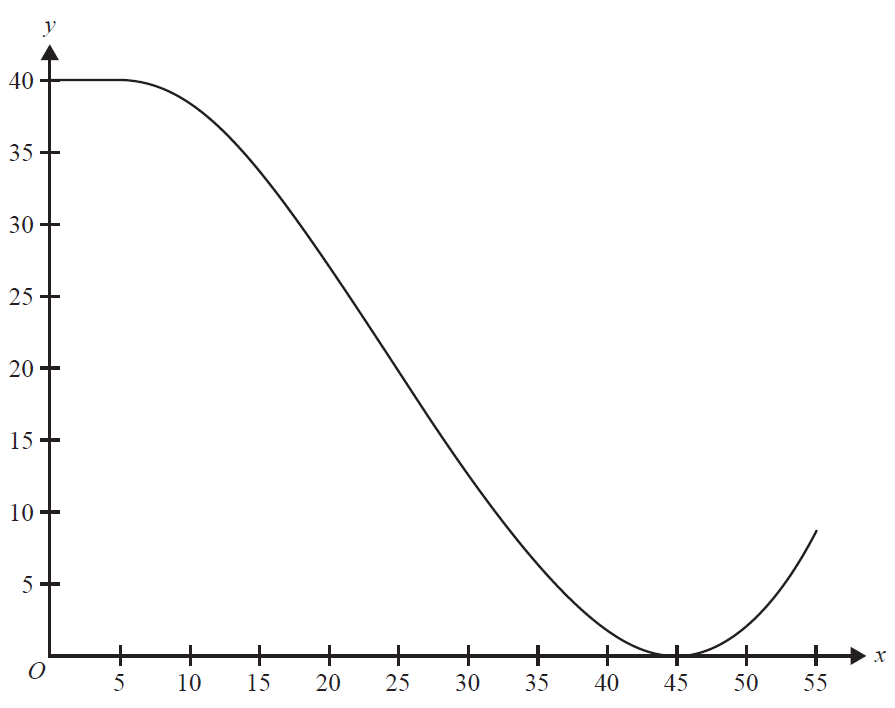
a. Find \(f'(x)\) for \(0 < x < 55\). 2 marks

b.

i. Find the coordinates of the point of inflection of \(f\). 1 mark

ii. Find the interval of \(x\) for which the gradient function of the ramp is strictly increasing. 1 mark

iii. Find the interval of \(x\) for which the gradient function of the ramp is strictly decreasing. 1 mark

Jac and Jill decide to use two trapezoidal supports, each of width 10 cm. The first support has its left edge placed at \(x = 5\) and the second support has its left edge placed at \(x = 15\). Their cross-sections are shown in the graph below.

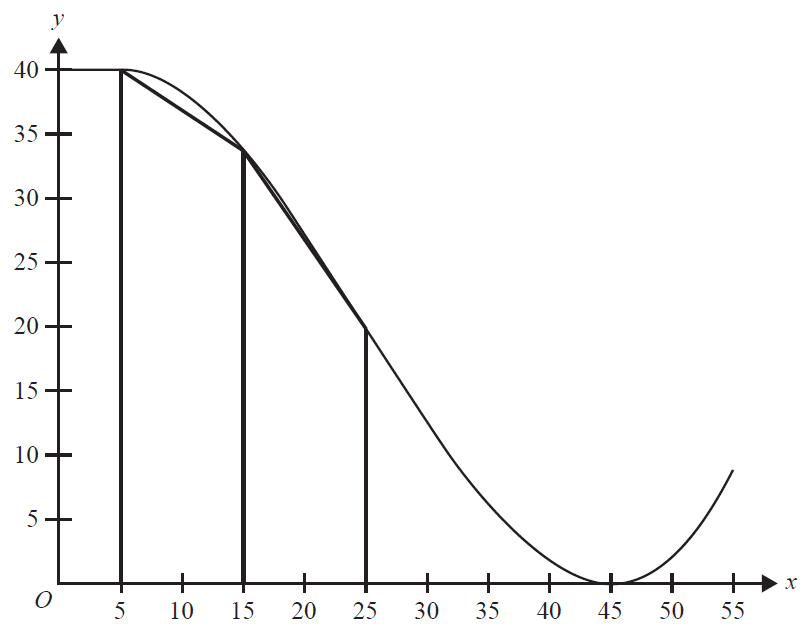
c. Determine the value of the ratio of the area of the trapezoidal cross-sections to the exact area contained between \(f(x)\) and the \(x\)-axis between \(x = 5\) and \(x = 25\). Give your answer as a percentage, correct to one decimal place. 3 marks

d. Referring to the gradient of the curve, explain why a trapezium rule approximation would be greater than the actual cross-sectional area for any interval \(x \in [p, q]\), where \(p \ge 25\). 1 mark

e. Jac and Jill roll the toy car down the ramp and the car jumps off the end of the ramp. The path of the car is modelled by the function \(P\), where

\( P(x) = \begin{cases} f(x) & 0 \le x \le 55 \\ g(x) & 55 < x \le a \end{cases} \)

\(P\) is continuous and differentiable at \(x = 55\), \(g(x) = -\frac{1}{16}x^2 + bx + c\), and \(x = a\) is where the car lands on the ground after the jump, such that \(P(a) = 0\).

i. Find the values of \(b\) and \(c\). 2 marks

ii. Determine the horizontal distance from the end of the ramp to where the car lands. Give your answer in centimetres, correct to two decimal places. 1 mark