2023 VCAA Maths Methods Sample Exam 1

Let \(f: [-3, -2) \cup (-2, \infty) \to \mathbb{R}, f(x) = 1 + \frac{1}{x+2}\).

a. On the axes below, sketch the graph of \(f\). Label any asymptotes with their equations, and endpoints and axial intercepts with their coordinates. 3 marks

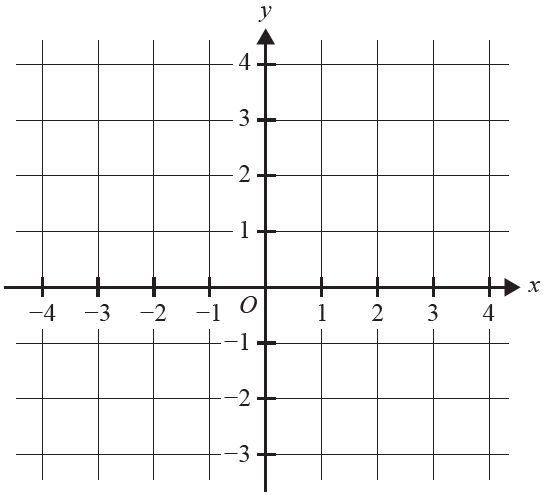
b. Find the values of \(x\) for which \(f(x) \le 2\). 2 marks

Consider the functions \(f\) and \(g\), where

\(f : \mathbb{R} \to \mathbb{R}, f(x) = x^2 - 9\)

\(g : [0, \infty) \to \mathbb{R}, g(x) = \sqrt{x}\)

a. State the range of \(f\). 1 mark

b. Determine the rule for the equation and state the domain of the function \(f \circ g\). 2 marks

c. Let \(h\) be the function \(h : D \to \mathbb{R}, h(x) = x^2 - 9\).

Determine the maximal domain, \(D\), such that \(g \circ h\) exists. 2 marks

Find the general solution for \(2\sin(x) = \tan(x)\) for \(x \in \mathbb{R}\). 3 marks

Consider the simultaneous equations below, where \(a\) and \(b\) are real constants.

\((a+3)x + 9y = 3b\)

\(2x + ay = 5\)

Find the values of \(a\) and \(b\) for which the simultaneous equations have no solutions. 4 marks

Let \(f: \mathbb{R} \to \mathbb{R}\), where \(f(x) = 2 - x^2\).

a. Calculate the average rate of change of \(f\) between \(x = -1\) and \(x = 1\). 1 mark

b. Calculate the average value of \(f\) between \(x = -1\) and \(x = 1\). 2 marks

c. Four trapeziums of equal width are used to approximate the area between the functions \(f(x) = 2 - x^2\) and the x-axis from \(x = -1\) to \(x = 1\).

The heights of the left and right edges of each trapezium are the values of \(y = f(x)\), as shown in the graph below.

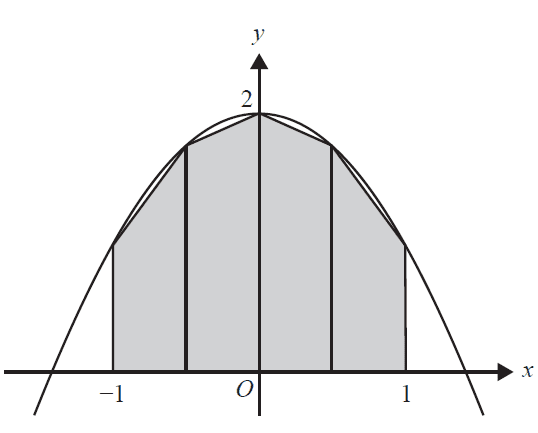
Find the total area of the four trapeziums. 3 marks

Newton's method is used to estimate the x-intercept of the function \(f(x) = \frac{1}{3}x^3 + 2x + 4\).

a. Verify that \(f(-1) > 0\) and \(f(-2) < 0\). 1 mark

b. Using an initial estimate of \(x_0 = -1\), find the value of \(x_1\). 2 marks

The duration of telemarketing calls to mobile phone users is a continuous random variable \(T\) minutes, with probability density function

\( f(t) = \begin{cases} \frac{2}{5}e^{-\frac{2}{5}t} & t \ge 0 \\ 0 & \text{elsewhere} \end{cases} \)

Find the value of \(k\) such that 90% of telemarketing calls last less than \(k\) minutes. Express your answer in the form \(\frac{a}{b}\log_e(c)\), where \(a\), \(b\) and \(c\) are positive integers. 3 marks