2023 VCAA Maths Methods Exam 1
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 40
Reading time: 15 minutes
Writing time: 1 hours
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Let \( y = \frac{x^2 - x}{e^x} \). Find and simplify \( \frac{dy}{dx} \). 2 marks
b. Let \( f(x) = \sin(x) e^{2x} \). Find \( f'\left( \frac{\pi}{4} \right) \). 2 marks
Solve \( e^{2x} - 12 = 4e^x \) for \( x \in \mathbb{R} \). 3 marks
a. Sketch the graph of \( f(x) = 2-\frac{3}{x - 1} \) on the axes below, labelling all asymptotes with their equations and axial intercepts with their coordinates. 3 marks
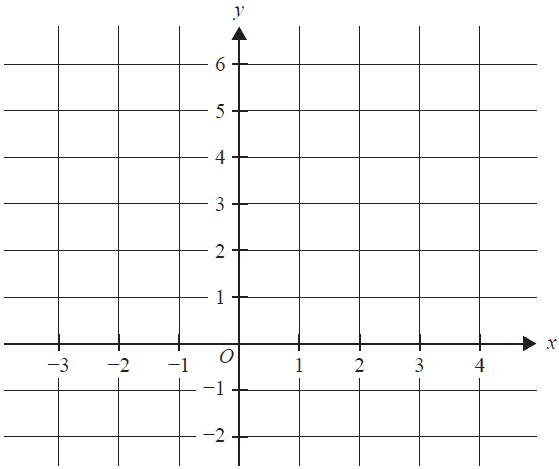
b. Find the values of \( x \) for which \( f(x) \leq 1 \). 1 mark
The graph of \( y = x + \frac{1}{x} \) is shown over part of its domain.
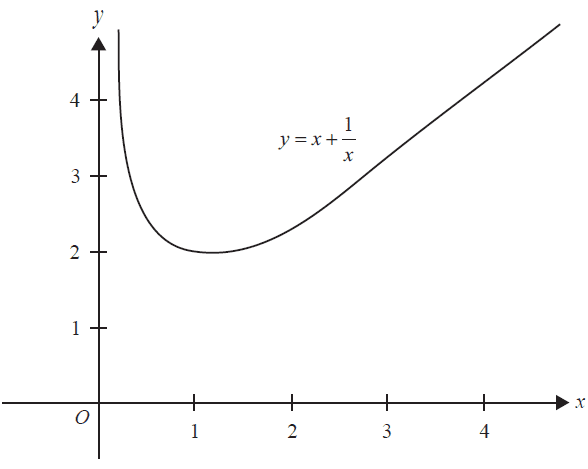
Use two trapeziums of equal width to approximate the area between the curve, the x-axis and the lines \( x = 1 \) and \( x = 3 \). 2 marks
a. Evaluate \( \int_{0}^{\frac{\pi}{3}} \sin(x) \, dx \). 1 mark
b. Hence, or otherwise, find all values of \( k \) such that \[ \int_{0}^{\frac{\pi}{3}} \sin(x) \, dx = \int_{k}^{\frac{\pi}{2}} \cos(x) \, dx, \] where \( -3\pi < k < 2\pi \). 3 marks
Let \( \hat{P} \) be the random variable that represents the sample proportion of households in a given suburb that have solar panels installed.
From a sample of randomly selected households in a given suburb, an approximate 95% confidence interval for the proportion \( p \) of households having solar panels installed was determined to be (0.04, 0.16).
a. Find the value of \( \hat{p} \) that was used to obtain this approximate 95% confidence interval. 1 mark
b. Find the size of the sample from which this 95% confidence interval was obtained.
Use \( z = 2 \) to approximate the 95% confidence interval. 2 marks
c. A larger sample of households is selected, with a sample size four times the original sample. The sample proportion of households having solar panels installed is found to be the same.
By what factor will the increased sample size affect the width of the confidence interval? 1 mark
Consider \( f : (-\infty, 1] \rightarrow \mathbb{R} \), \( f(x) = x^2 - 2x \). Part of the graph of \( y = f(x) \) is shown below.
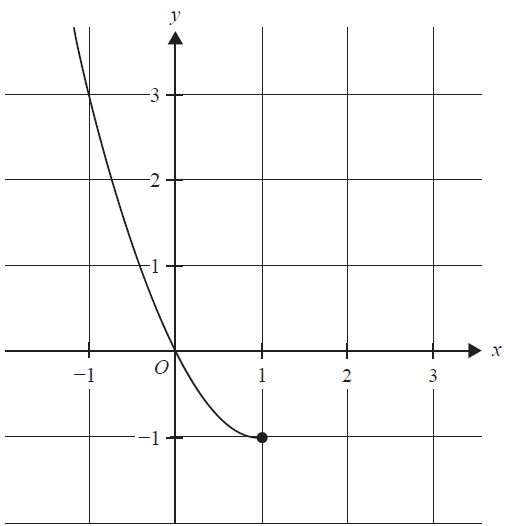
a. State the range of \( f \). 1 mark
b. Sketch the graph of the inverse function \( y = f^{-1}(x) \) on the axes above. Label any endpoints and axial intercepts with their coordinates. 2 marks
c. Determine the equation and the domain for the inverse function \( f^{-1} \). 2 marks
d. Calculate the area of the regions enclosed by the curves of \( f \), \( f^{-1} \) and \( y = -x \). 2 marks
Suppose that the queuing time, \( T \) (in minutes), at a customer service desk has a probability density function given by
\[ f(t) = \begin{cases} kt(16 - t^2) & 0 \leq t \leq 4 \\ 0 & \text{elsewhere} \end{cases} \] for some \( k \in \mathbb{R} \).
a. Show that \( k = \frac{1}{64} \). 1 mark
b. Find \( E(T) \). 2 marks
c. What is the probability that a person has to queue for more than two minutes, given that they have already queued for one minute? 3 marks
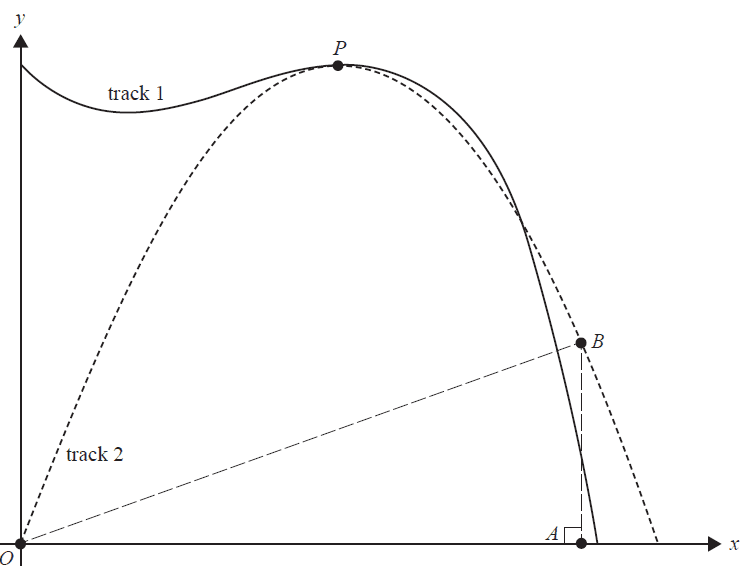
The shapes of two walking tracks are shown below.
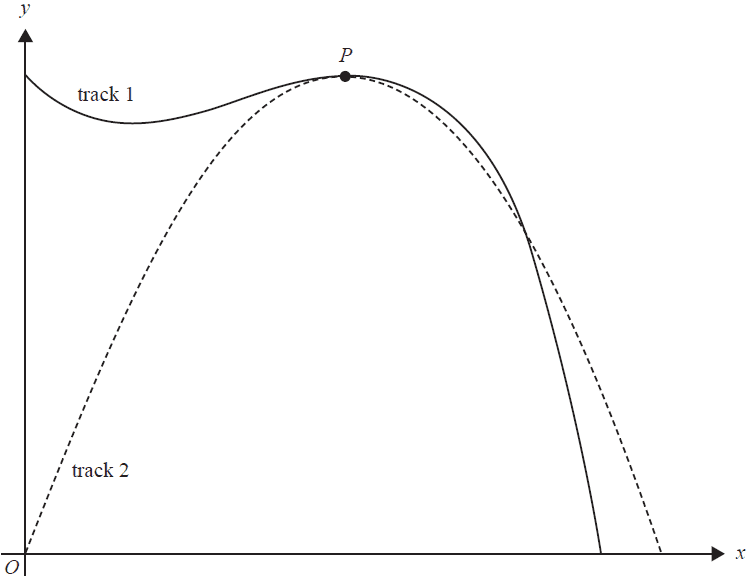
Track 1 is described by the function \( f(x) = a - x(x - 2)^2 \).
Track 2 is defined by the function \( g(x) = 12x + bx^2 \).
The unit of length is kilometres.
a. Given that \( f(0) = 12 \) and \( g(1) = 9 \), verify that \( a = 12 \) and \( b = -3 \). 1 mark
b. Verify that \( f(x) \) and \( g(x) \) both have a turning point at \( P \).
Give the coordinates of \( P \). 2 marks
c. A theme park is planned whose boundaries will form the triangle \( \triangle OAB \) where \( O \) is the origin, \( A \) is at \( (k, 0) \) and \( B \) is at \( (k, g(k)) \), as shown below, where \( k \in (0, 4) \).
Find the maximum possible area of the theme park, in km\(^2\). 3 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

