2016 VCAA Maths Methods Exam 2

Question 1 [2016 Exam 2 Section A Q1]

The linear function \(f: D \to R, f(x) = 5 - x\) has range \([-4, 5)\).
The domain \(D\) is

• A. \((0, 9]\)
• B. \((0, 1]\)
• C. \([5, -4)\)
• D. \([-9, 0)\)
• E. \([1, 9)\)

Question 2 [2016 Exam 2 Section A Q2]

Let \(f: R \to R, f(x) = 1 - 2\cos\left(\frac{\pi x}{2}\right)\).
The period and range of this function are respectively

• A. 4 and \([-2, 2]\)
• B. 4 and \([-1, 3]\)
• C. 1 and \([-1, 3]\)
• D. \(4\pi\) and \([-1, 3]\)
• E. \(4\pi\) and \([-2, 2]\)

Question 3 [2016 Exam 2 Section A Q3]

Part of the graph \(y = f(x)\) of the polynomial function \(f\) is shown below.

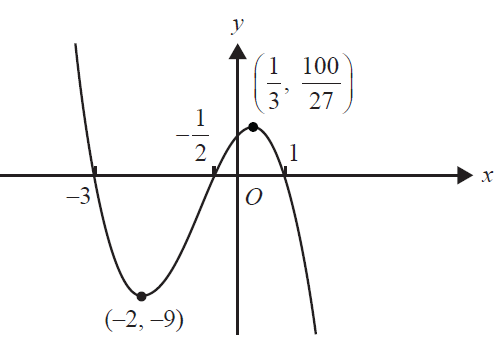
\(f'(x) < 0\) for

• A. \(x \in (-2, 0) \cup (\frac{1}{3}, \infty)\)
• B. \(x \in (-9, \frac{100}{27})\)
• C. \(x \in (-\infty, -2) \cup (\frac{1}{3}, \infty)\)
• D. \(x \in (-2, \frac{1}{3})\)
• E. \(x \in (-\infty, -2] \cup (1, \infty)\)

Question 4 [2016 Exam 2 Section A Q4]

The average rate of change of the function \(f\) with rule \(f(x) = 3x^2 - 2\sqrt{x+1}\), between \(x=0\) and \(x=3\), is

• A. 8
• B. 25
• C. \(\frac{53}{9}\)
• D. \(\frac{25}{3}\)
• E. \(\frac{13}{9}\)

Question 5 [2016 Exam 2 Section A Q5]

Which one of the following is the inverse function of \(g: [3, \infty) \to R, g(x) = \sqrt{2x-6}\)?

• A. \(g^{-1}: [3, \infty) \to R, g^{-1}(x) = \frac{x^2+6}{2}\)
• B. \(g^{-1}: [0, \infty) \to R, g^{-1}(x) = (2x-6)^2\)
• C. \(g^{-1}: [0, \infty) \to R, g^{-1}(x) = \sqrt{\frac{x}{2}+6}\)
• D. \(g^{-1}: [0, \infty) \to R, g^{-1}(x) = \frac{x^2+6}{2}\)
• E. \(g^{-1}: R \to R, g^{-1}(x) = \frac{x^2+6}{2}\)

Question 6 [2016 Exam 2 Section A Q6]

Consider the graph of the function defined by \(f: [0, 2\pi] \to R, f(x) = \sin(2x)\).
The square of the length of the line segment joining the points on the graph for which \(x = \frac{\pi}{4}\) and \(x = \frac{3\pi}{4}\) is

• A. \(\frac{\pi^2+16}{4}\)
• B. \(\pi+4\)
• C. 4
• D. \(\frac{3\pi^2+16\pi}{4}\)
• E. \(\frac{10\pi^2}{16}\)

Question 7 [2016 Exam 2 Section A Q7]

The number of pets, \(X\), owned by each student in a large school is a random variable with the following discrete probability distribution.

\(x\)	0	1	2	3
\(\Pr(X=x)\)	0.5	0.25	0.2	0.05

If two students are selected at random, the probability that they own the same number of pets is

• A. 0.3
• B. 0.305
• C. 0.355
• D. 0.405
• E. 0.8

Question 8 [2016 Exam 2 Section A Q8]

The UV index, \(y\), for a summer day in Melbourne is illustrated in the graph below, where \(t\) is the number of hours after 6 am.

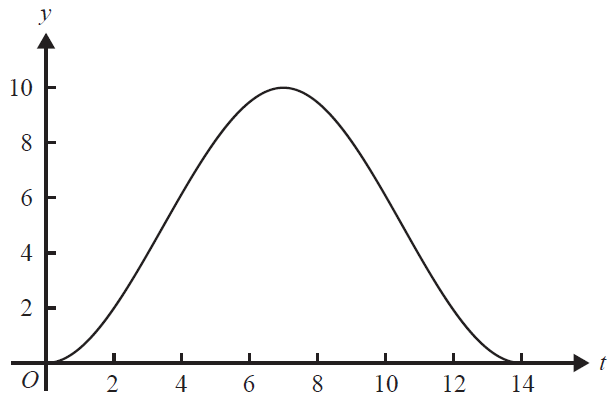
The graph is most likely to be the graph of

• A. \(y = 5 + 5\cos\left(\frac{\pi t}{7}\right)\)
• B. \(y = 5 - 5\cos\left(\frac{\pi t}{7}\right)\)
• C. \(y = 5 + 5\cos\left(\frac{\pi t}{14}\right)\)
• D. \(y = 5 - 5\cos\left(\frac{\pi t}{14}\right)\)
• E. \(y = 5 + 5\sin\left(\frac{\pi t}{14}\right)\)

Question 9 [2016 Exam 2 Section A Q9]

Given that \(\frac{d(xe^{kx})}{dx}) = (kx+1)e^{kx}\), then \(\int xe^{kx} dx\) is equal to

• A. \(\frac{xe^{kx}}{kx+1} + c\)
• B. \((\frac{kx+1}{k})e^{kx} + c\)
• C. \(\frac{1}{k}\int e^{kx} dx\)
• D. \(\frac{1}{k}(xe^{kx} - \int e^{kx} dx) + c\)
• E. \(\frac{1}{k^2}(xe^{kx} - e^{kx}) + c\)

Question 10 [2016 Exam 2 Section A Q10]

For the curve \(y = x^2 - 5\), the tangent to the curve will be parallel to the line connecting the positive \(x\)-intercept and the \(y\)-intercept when \(x\) is equal to

• A. \(\sqrt{5}\)
• B. 5
• C. -5
• D. \(\frac{\sqrt{5}}{2}\)
• E. \(\frac{1}{\sqrt{5}}\)

Question 11 [2016 Exam 2 Section A Q11]

The function \(f\) has the property \(f(x) - f(y) = (y-x)f(xy)\) for all non-zero real numbers \(x\) and \(y\).
Which one of the following is a possible rule for the function?

• A. \(f(x) = x^2\)
• B. \(f(x) = x^2 + x^4\)
• C. \(f(x) = x\log_e(x)\)
• D. \(f(x) = \frac{1}{x}\)
• E. \(f(x) = \frac{1}{x^2}\)

Question 12 [2016 Exam 2 Section A Q12]

The graph of a function \(f\) is obtained from the graph of the function \(g\) with rule \(g(x) = \sqrt{2x-5}\) by a reflection in the \(x\)-axis followed by a dilation from the \(y\)-axis by a factor of \(\frac{1}{2}\).
Which one of the following is the rule for the function \(f\)?

• A. \(f(x) = \sqrt{5-4x}\)
• B. \(f(x) = -\sqrt{x-5}\)
• C. \(f(x) = \sqrt{x+5}\)
• D. \(f(x) = -\sqrt{4x-5}\)
• E. \(f(x) = -\sqrt{4x-10}\)

Question 13 [2016 Exam 2 Section A Q13]

Consider the graphs of the functions \(f\) and \(g\) shown below.

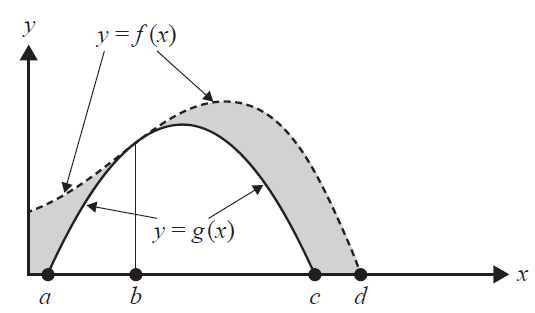
The area of the shaded region could be represented by

• A. \(\int_a^d (f(x)-g(x))dx\)


• B. \(\int_0^d (f(x)-g(x))dx\)


• C. \(\int_0^b (f(x)-g(x))dx + \int_b^c (f(x)-g(x))dx\)


• D. \(\int_0^a f(x)dx + \int_a^c (f(x)-g(x))dx+\int_b^d f(x)dx \)


• E. \(\int_0^d f(x)dx - \int_a^c g(x)dx\)

Question 14 [2016 Exam 2 Section A Q14]

A rectangle is formed by using part of the coordinate axes and a point \((u, v)\), where \(u > 0\) on the parabola \(y = 4-x^2\).

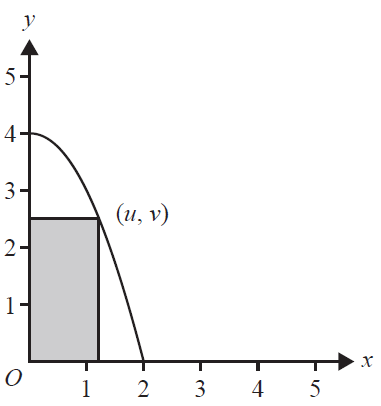
Which one of the following is the maximum area of the rectangle?

• A. 4
• B. \(\frac{2\sqrt{3}}{3}\)
• C. \(\frac{8\sqrt{3}-4}{3}\)
• D. \(\frac{8}{3}\)
• E. \(\frac{16\sqrt{3}}{9}\)

Question 15 [2016 Exam 2 Section A Q15]

A box contains six red marbles and four blue marbles. Two marbles are drawn from the box, without replacement.
The probability that they are the same colour is

• A. \(\frac{1}{2}\)
• B. \(\frac{28}{45}\)
• C. \(\frac{7}{15}\)
• D. \(\frac{3}{5}\)
• E. \(\frac{1}{3}\)

Question 16 [2016 Exam 2 Section A Q16]

The random variable, \(X\), has a normal distribution with mean 12 and standard deviation 0.25.
If the random variable, \(Z\), has the standard normal distribution, then the probability that \(X\) is greater than 12.5 is equal to

• A. \(\Pr(Z < -4)\)
• B. \(\Pr(Z < -1.5)\)
• C. \(\Pr(Z < 1)\)
• D. \(\Pr(Z \ge 1.5)\)
• E. \(\Pr(Z > 2)\)

Question 17 [2016 Exam 2 Section A Q17]

Inside a container there are one million coloured building blocks. It is known that 20% of the blocks are red. A sample of 16 blocks is taken from the container. For samples of 16 blocks, \(\hat{P}\) is the random variable of the distribution of sample proportions of red blocks. (Do not use a normal approximation.)
\(\Pr(\hat{P} \ge \frac{3}{16})\) is closest to

• A. 0.6482
• B. 0.8593
• C. 0.7543
• D. 0.6542
• E. 0.3211

Question 18 [2016 Exam 2 Section A Q18]

The continuous random variable, \(X\), has a probability density function given by

\(f(x) = \begin{cases} \frac{1}{4}\cos\left(\frac{x}{2}\right) & 3\pi \le x \le 5\pi \\ 0 & \text{elsewhere} \end{cases} \)

The value of \(a\) such that \(\Pr(X < a) = \frac{\sqrt{3}+2}{4}\) is

• A. \(\frac{19\pi}{6}\)
• B. \(\frac{14\pi}{3}\)
• C. \(\frac{10\pi}{3}\)
• D. \(\frac{29\pi}{6}\)
• E. \(\frac{17\pi}{3}\)

Question 19 [2016 Exam 2 Section A Q19]

Consider the discrete probability distribution with random variable \(X\) shown in the table below.

\(x\)	-1	0	\(b\)	\(2b\)	4
\(\Pr(X=x)\)	\(a\)	\(b\)	\(b\)	\(2b\)	0.2

The smallest and largest possible values of \(E(X)\) are respectively

• A. -0.8 and 1
• B. -0.8 and 1.6
• C. 0 and 2.4
• D. 0.2125 and 1
• E. 0 and 1

Question 20 [2016 Exam 2 Section A Q20]

Consider the transformation \(T\), defined as

\(T: R^2 \to R^2, T\left(\begin{bmatrix} x \\ y \end{bmatrix}\right) = \begin{bmatrix} -1 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 0 \\ 5 \end{bmatrix} \)

The transformation \(T\) maps the graph of \(y = f(x)\) onto the graph of \(y = g(x)\).
If \(\int_0^3 f(x)dx = 5\), then \(\int_{-3}^0 g(x)dx\) is equal to

• A. 0
• B. 15
• C. 20
• D. 25
• E. 30

Question 1 [2016 Exam 2 Section B Q1]

Let \(f: [0, 8\pi] \to R, f(x) = 2\cos\left(\frac{x}{2}\right) + \pi\).

a. Find the period and range of \(f\). 2 marks

b. State the rule for the derivative function \(f'\). 1 mark

c. Find the equation of the tangent to the graph of \(f\) at \(x = \pi\). 1 mark

d. Find the equations of the tangents to the graph of \(f: [0, 8\pi] \to R, f(x) = 2\cos\left(\frac{x}{2}\right) + \pi\) that have a gradient of 1. 2 marks

e. The rule of \(f'\) can be obtained from the rule of \(f\) under a transformation \(T\), such that \(T: R^2 \to R^2, T\left(\begin{bmatrix} x \\ y \end{bmatrix}\right) = \begin{bmatrix} 1 & 0 \\ 0 & a \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} -\pi \\ b \end{bmatrix} \) Find the value of \(a\) and the value of \(b\). 3 marks

f. Find the values of \(x, 0 \le x \le 8\pi\), such that \(f(x) = 2f'(x) + \pi\). 2 marks

Question 2 [2016 Exam 2 Section B Q2]

Consider the function \(f(x) = -\frac{1}{3}(x+2)(x-1)^2\).

a.

i. Given that \(g'(x) = f(x)\) and \(g(0) = 1\), show that \(g(x) = -\frac{x^4}{12} + \frac{x^2}{2} - \frac{2x}{3} + 1\). 1 mark

ii. Find the values of \(x\) for which the graph of \(y = g(x)\) has a stationary point. 1 mark

b. The diagram below shows part of the graph of \(y = g(x)\), the tangent to the graph at \(x = 2\) and a straight line drawn perpendicular to the tangent to the graph at \(x = 2\). The equation of the tangent at the point \(A\) with coordinates \((2, g(2))\) is \(y = 3 - \frac{4x}{3}\).
The tangent cuts the \(y\)-axis at \(B\). The line perpendicular to the tangent cuts the \(y\)-axis at \(C\).

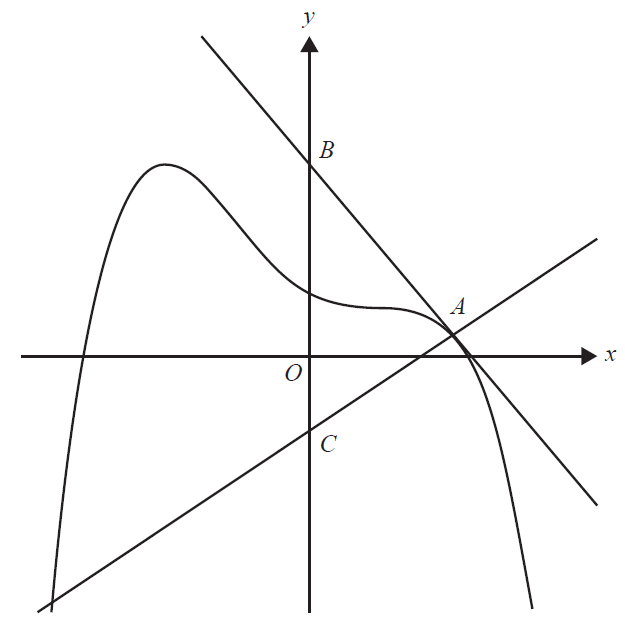
i. Find the coordinates of \(B\). 1 mark

ii. Find the equation of the line that passes through \(A\) and \(C\) and, hence, find the coordinates of \(C\). 2 marks

iii. Find the area of triangle \(ABC\). 2 marks

c. The tangent at \(D\) is parallel to the tangent at \(A\). It intersects the line passing through \(A\) and \(C\) at \(E\).

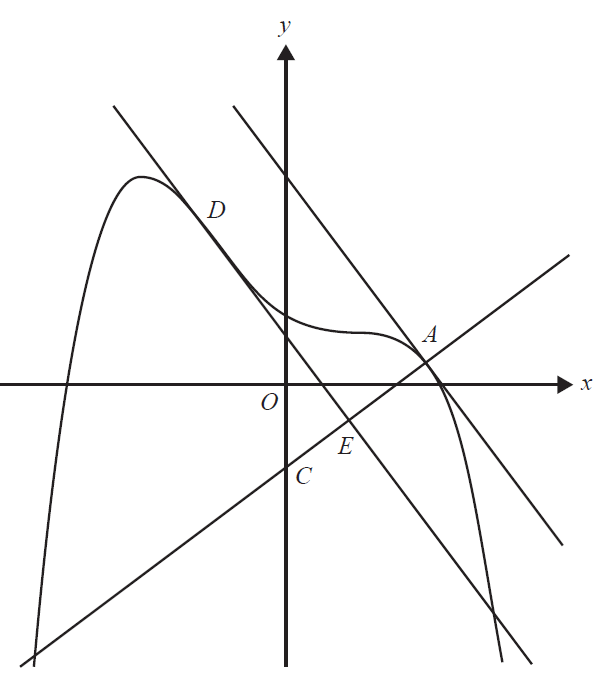
i. Find the coordinates of \(D\). 2 marks

ii. Find the length of \(AE\). 3 marks

Question 3 [2016 Exam 2 Section B Q3]

A school has a class set of 22 new laptops kept in a recharging trolley. Provided each laptop is correctly plugged into the trolley after use, its battery recharges.
On a particular day, a class of 22 students uses the laptops. All laptop batteries are fully charged at the start of the lesson. Each student uses and returns exactly one laptop. The probability that a student does not correctly plug their laptop into the trolley at the end of the lesson is 10%. The correctness of any student's plugging-in is independent of any other student's correctness.

a. Determine the probability that at least one of the laptops is not correctly plugged into the trolley at the end of the lesson. Give your answer correct to four decimal places. 2 marks

b. A teacher observes that at least one of the returned laptops is not correctly plugged into the trolley.
Given this, find the probability that fewer than five laptops are not correctly plugged in. Give your answer correct to four decimal places. 2 marks

c. The time for which a laptop will work without recharging (the battery life) is normally distributed, with a mean of three hours and 10 minutes and standard deviation of six minutes. Suppose that the laptops remain out of the recharging trolley for three hours.
For any one laptop, find the probability that it will stop working by the end of these three hours. Give your answer correct to four decimal places. 2 marks

d. A supplier of laptops decides to take a sample of 100 new laptops from a number of different schools. For samples of size 100 from the population of laptops with a mean battery life of three hours and 10 minutes and standard deviation of six minutes, \(\hat{P}\) is the random variable of the distribution of sample proportions of laptops with a battery life of less than three hours.
Find the probability that \(\Pr(\hat{P} \ge 0.06 | \hat{P} \ge 0.05)\). Give your answer correct to three decimal places. Do not use a normal approximation. 3 marks

e. It is known that when laptops have been used regularly in a school for six months, their battery life is still normally distributed but the mean battery life drops to three hours. It is also known that only 12% of such laptops work for more than three hours and 10 minutes.
Find the standard deviation for the normal distribution that applies to the battery life of laptops that have been used regularly in a school for six months, correct to four decimal places. 2 marks

f. The laptop supplier collects a sample of 100 laptops that have been used for six months from a number of different schools and tests their battery life. The laptop supplier wishes to estimate the proportion of such laptops with a battery life of less than three hours.
Suppose the supplier tests the battery life of the laptops one at a time.
Find the probability that the first laptop found to have a battery life of less than three hours is the third one. 1 mark

g. The laptop supplier finds that, in a particular sample of 100 laptops, six of them have a battery life of less than three hours.
Determine the 95% confidence interval for the supplier's estimate of the proportion of interest. Give values correct to two decimal places. 1 mark

h. The supplier also provides laptops to businesses. The probability density function for battery life, \(x\) (in minutes), of a laptop after six months of use in a business is \(f(x) = \begin{cases} \frac{(210-x)e^{\frac{x-210}{20}}}{400} & 0 \le x \le 210 \\ 0 & \text{elsewhere} \end{cases}\)

i. Find the mean battery life, in minutes, of a laptop with six months of business use, correct to two decimal places. 1 mark

ii. Find the median battery life, in minutes, of a laptop with six months of business use, correct to two decimal places. 2 marks

Question 4 [2016 Exam 2 Section B Q4]

a. Express \(\frac{2x+1}{x+2}\) in the form \(a + \frac{b}{x+2}\), where \(a\) and \(b\) are non-zero integers. 2 marks

b. Let \(f: R \setminus \{-2\} \to R, f(x) = \frac{2x+1}{x+2}\).

i. Find the rule and domain of \(f^{-1}\), the inverse function of \(f\). 2 marks

ii. Part of the graphs of \(f\) and \(y = x\) are shown in the diagram below.

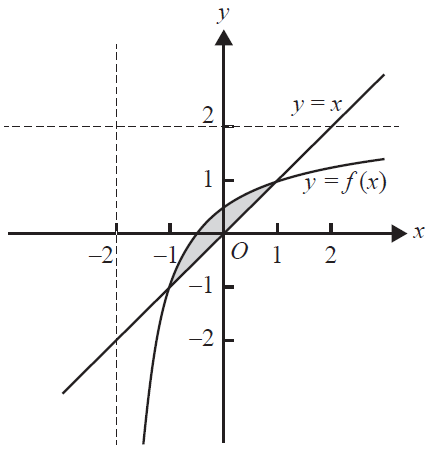
Find the area of the shaded region. 1 mark

iii. Part of the graphs of \(f\) and \(f^{-1}\) are shown in the diagram below.

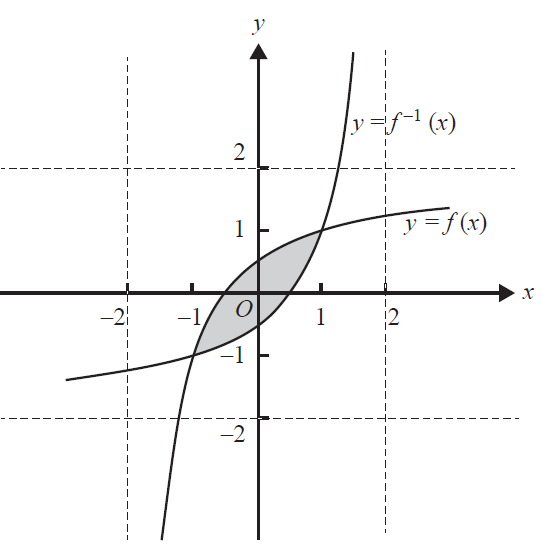
Find the area of the shaded region. 1 mark

c. Part of the graph of \(f\) is shown in the diagram below.

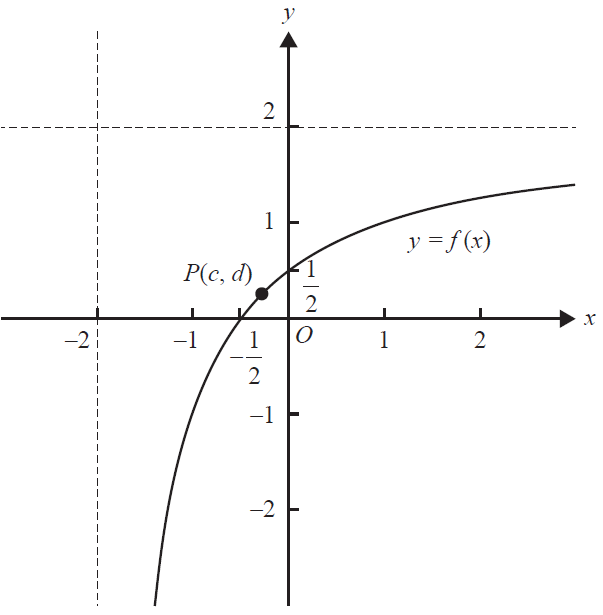
The point \(P(c, d)\) is on the graph of \(f\).
Find the exact values of \(c\) and \(d\) such that the distance of this point to the origin is a minimum, and find this minimum distance. 3 marks

d. Let \(g: (-k, \infty) \to R, g(x) = \frac{kx+1}{x+k}\), where \(k > 1\).
Show that \(x_1 < x_2\) implies that \(g(x_1) < g(x_2)\), where \(x_1 \in (-k, \infty)\) and \(x_2 \in (-k, \infty)\). 2 marks

e.

i. Let \(X\) be the point of intersection of the graphs of \(y = g(x)\) and \(y = -x\).
Find the coordinates of \(X\) in terms of \(k\). 2 marks

ii. Find the value of \(k\) for which the coordinates of \(X\) are \((-\frac{1}{2}, \frac{1}{2})\). 2 marks

iii. Let \(Z(-1, -1)\), \(Y(1, 1)\) and \(X\) be the vertices of the triangle \(XYZ\). Let \(s(k)\) be the square of the area of triangle \(XYZ\).

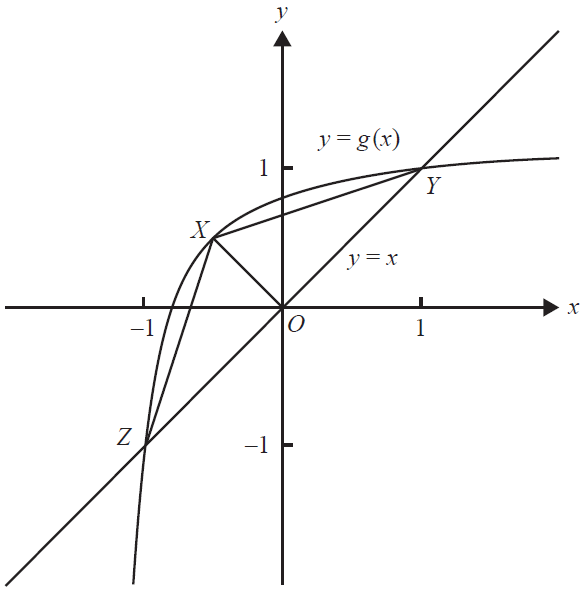
Find the values of \(k\) such that \(s(k) \ge 1\). 2 marks

f. The graph of \(g\) and the line \(y = x\) enclose a region of the plane. The region is shown shaded in the diagram below.

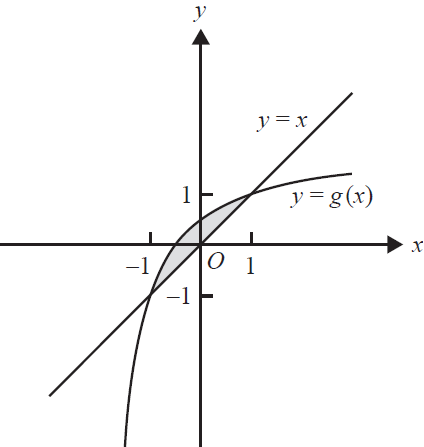
Let \(A(k)\) be the rule of the function \(A\) that gives the area of this enclosed region. The domain of \(A\) is \((1, \infty)\).

i. Give the rule for \(A(k)\). 2 marks

ii. Show that \(0 < A(k) < 2\) for all \(k > 1\). 2 marks